† Corresponding author. E-mail:
Project supported by the Science and Technology Development Fund Planning Project for the Universities of Tianjin, China (Grant No. 20140902), the Natural Science Foundation of Tianjin City, China (Grant No. 16JCQNJC01900), the National Natural Science Foundation of China (Grant Nos. 51376136 and 61474082), and the Science and Technology Achievement Award Project for the Universities of Tianjin, China.
Aluminum ablation by multiple femtosecond laser pulses is investigated via time-resolved shadowgraphs and scanning electron microscope (SEM) images of the ablation spot. The spatial distribution of the ejected material and the radius of the shock wave generated during the ablation are found to vary with the increase in the number of pulses. In the initial two pulses, nearly concentric and semicircular stripes within the shock wave front are observed, unlike in subsequent pulses. Ablation by multiple femtosecond pulses exhibits different characteristics compared with the case induced by single femtosecond pulse because of the changes to the aluminum target surface induced by the preceding pulses.
Femtosecond laser ablation has important applications in many scientific and engineering fields, such as nano-and micro-machining,[1–8] surface modification,[9–12] and nanoparticle generation.[13–15] Many theories have been proposed to explain the physical mechanisms of femtosecond laser ablation, including phase explosion,[16] critical point phase separation,[17] Coulomb explosion,[18] fragmentation,[19] and thermoelastic waves.[20] However, the difference between single-pulse ablation and multi-pulse ablation by femtosecond laser has not been sufficiently investigated, and this should be remedied because ablation by multiple femtosecond pulses exhibits different characteristics compared with the case induced by single femtosecond pulse, which is notable for the applications of femtosecond laser ablation.
When multiple pulses irradiate the same spot on the target surface, it has been reported that the ablation threshold decreases with the increase in the number of femtosecond laser pulses,[21,22] which is known as the incubation effect. A few previous works on ablation by multiple femtosecond laser pulses have mainly concentrated on the morphology of the ablated spot.[21–25] However, the material ejection and shock wave evolution are also notable experimental phenomena in this process, and some works have investigated the shock wave and the ejected material and got some helpful results.[26–31] Therefore, in combination with the morphology analyses, the investigation of the ultrafast dynamics of the material ejection and shock wave evolution induced by a sequence of femtosecond laser pulses presented in this paper elucidates the mechanisms of multiple femtosecond pulses ablation.
This study recorded the dynamic evolution process of the shock wave and ejected material induced by aluminum ablation with multiple femtosecond laser pulses via time-resolved shadowgraphs, and the morphology of the ablated spots was observed with a scanning electron microscope (SEM). The radius of the shock wave and the spatial distribution of the ejected material were found to vary with the increase in the number of femtosecond laser pulses at specific delay time after the target was irradiated by a laser pulse. In addition, in the initial two femtosecond laser pulses only, nearly concentric and semicircular stripes within the shock wave front were observed in the shadowgraphs recorded at a delay time of 2 ns. Solidified aluminum droplets were observed at the ablated spot, indicating the occurrence of thermal effect in the process of the femtosecond laser ablation in our experiments.
A Ti:Sapphire femtosecond laser amplifier system (HP-Spitfire, Spectra-Physics, Inc.) was employed to generate 50-fs laser pulses with a central wavelength of 800 nm. The schematic of the experiment setup is shown in Fig.
 | Fig. 1. (color online) Experimental setup for recording the ultrafast time-resolved shadowgraphs of femtosecond laser ablation of aluminum. |
The aluminum target was polished with #2000 sandpaper and mounted on a three-dimensional motor-controlled translation stage. The pump laser pulse energy was 0.22 mJ. The corresponding laser fluence at the focal point of the off-axis parabolic mirror was sufficiently high to ionize the ambient air. To avoid the air ionization, when the shadowgraphs of the femtosecond laser ablation were recorded, the aluminum target was placed slightly in front of the air ionization region, as shown by the target top view in Fig.
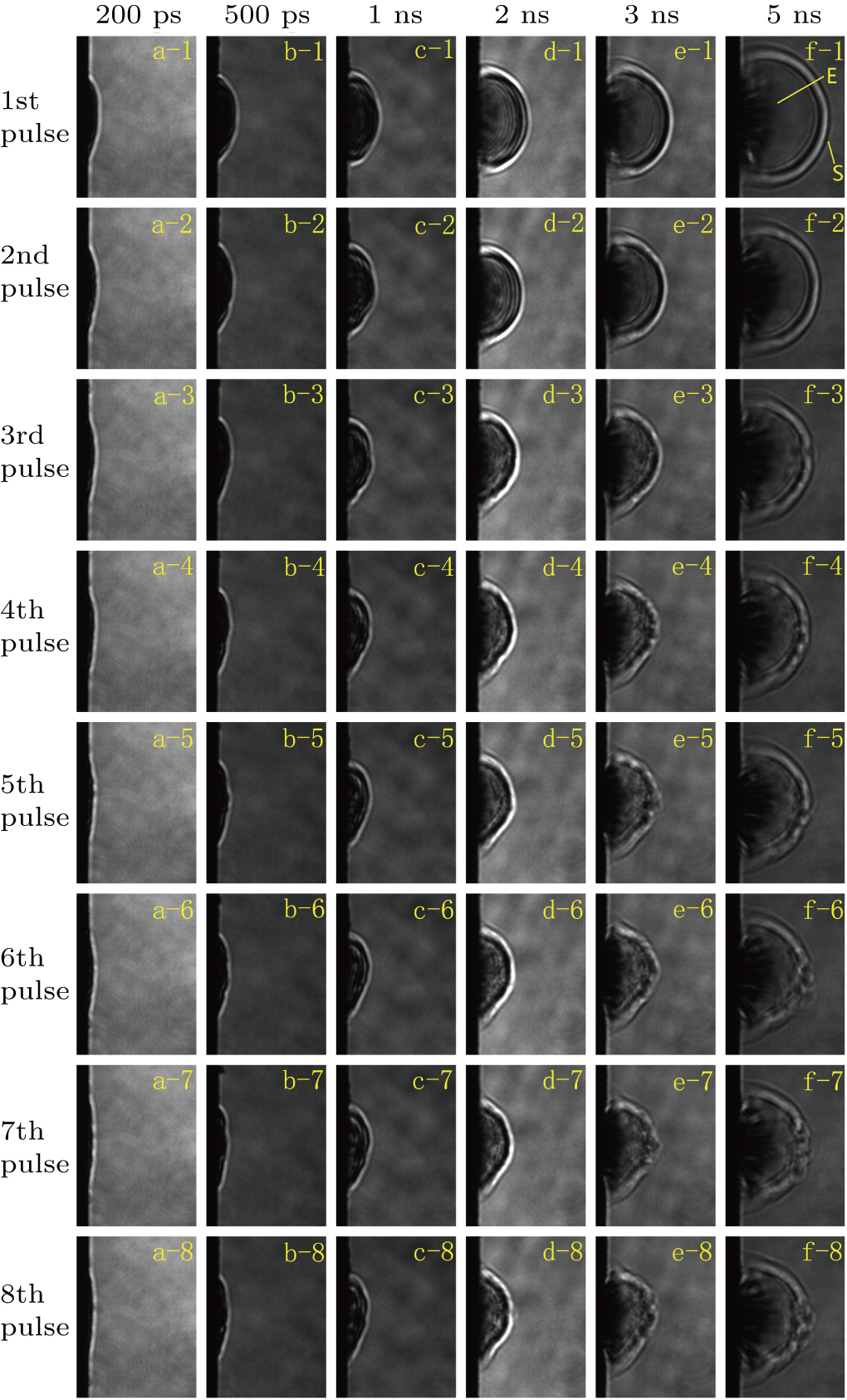
Figure
The shadowgraphs in the first row of Fig.
Comparing the shadowgraphs in the first row with those in the other rows of Fig.
The estimated fluence of the femtosecond laser on the aluminum target surface is 5.3 J/cm2, and the power density is approximately 1.06 × 1014 W/cm2. The fluence on the aluminum target surface is higher than the ablation threshold of aluminum in air (approximately 0.1 J/cm2),[32] and such a power density will induce the ionization of the surface layer atoms of the aluminum target and form plasma.[19,33] The bulge that appears at 200-ps delay time is the plasma generated because of the ionization of the atoms in the aluminum target’s surface layers, induced by the high-intensity laser energy deposited at the surface of the target. At the 200-ps delay time, the plasma bulge is opaque, as shown by Fig.
The plasma of the shock wave becomes transparent after 3 ns, and the ejected material can be clearly observed within the shock wave front after 3 ns, as shown in Fig.
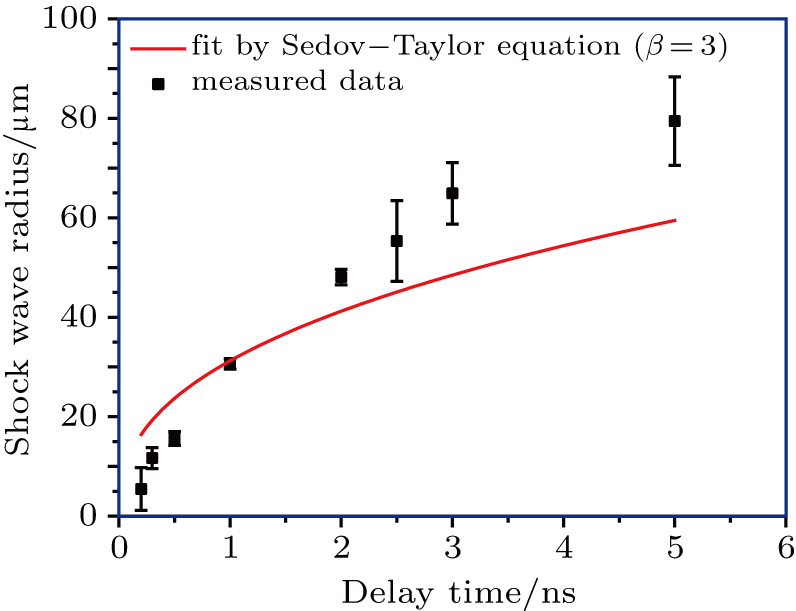
The dependence of the radius R of the shock wave front on the propagation time or delay time can be approximately described by the Sedov–Taylor equation[34,35]
 |
Figure
The air pressure just behind the shock wave front is also estimated with the following equation developed from Sedov’s theory:[34]
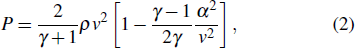 |
The calculated air pressure behind the shock wave front at different delay times is shown in Fig.
 | Fig. 5. Calculated air pressure just behind the shock wave front as a function of delay time under 1 atm. |
Changes to the target surface induced by the laser pulses ablation can certainly be expected to be responsible for the differences between multi-pulse ablation and single-pulse ablation. The SEM images in Fig.
At the same time, the preceding laser pulse ablation will also generate some aluminum oxide film of high transmittance on the target surface. As a result, the more energy of the subsequent laser pulse deposits in the interior of the target and the intensity deposited at the surface layer decreases, which results in the weakness of the ionization of the surface layer atoms. The material under the film of high transmittance can be ionized by the incident laser pulse. However, the film of high transmittance becomes an obstruction and attenuates the expansion of the plasma generated by the ionization of the material under the film of high transmittance, which results in the decrease of the energy driving the shock wave, and therefore the radius of the shockwave front decreases with the increase in the ablation laser pulse ordinal.
The less energy drives the shock wave, the smaller the radius of the shock wave is at any given delay time. Before the fourth laser pulse, the change to the target surface structure is significant, as shown in Fig.
When the femtosecond laser irradiates the aluminum target, the intensity of the laser deposited at a given depth in the aluminum target follows the Beer–Lambert law that the intensity decreases with increasing penetration depth. Therefore, the atoms in the depth of the aluminum target cannot ionize directly in the manner of the target’s surface layer atoms because of the decreased laser intensity. The deposition of the laser pulse energy in the depth of the aluminum target generates the ejected material indicated by E in Fig.
Figure
Previous works have reported that the optical absorption of the metal surface was enhanced by the micro- and nanostructures induced by the femtosecond laser.[36–38] The ablation induced by the preceding pulse generates micro- and nano-structures on the target surface, leading to more laser energy absorbed by the target for the second laser ablation. The enhanced absorption provided by these surface structures facilitates increased energy transfer to the aluminum lattice during the second femtosecond laser ablation, increasing the amount and velocity of ejected material.
It is also reported that the high pressure of the shock wave induces residual stress in the materials after the material is treated by the laser shock processing.[39–41] In our experiment, the estimated plasma pressure of shock wave is 1.52 GPa at 200-ps delay time, as shown in Fig.
The target surface structure continues to change with the each subsequent laser pulse. The surface structure of the aluminum target after the fourth or the eighth pulses ablation are different with that after first or the second laser ablation, resulting in different spatial distributions and the amounts and velocity of material ejected by the pulses. The amount and velocity of the ejected material vary with the increase of the laser pulse ordinal, which should be considered in the process of femtosecond laser machining.
In single-pulse ablation, several nearly concentric and semicircular stripes occur at approximately 2-ns delay time, and the stripes blur at 3 ns and disappear entirely at 5 ns, as shown by the first row of Fig.
In Figs.
The dynamic evolution process of aluminum ablation by successive femtosecond laser pulses is investigated using time-resolved shadowgraphs based on the pump–probe technique, as well as morphology analyses using SEM images. The spatial distribution of the ejected material varies with increasing numbers of incident laser pulses. The area and distance covered by the ejected material in the interior of the shock wave by the second pulse are larger than that ejected by the first pulse in shadowgraphs, indicating that more and higher speed material is ejected by the second pulse than by the first pulse. The radius of the induced shock wave decreases over the initial four laser pulses, and then remains almost unchanged after the fourth laser pulse. Nearly concentric and semicircular stripes are observed within the shock wave front for the first and second pulses in shadowgraphs, and the stripes blur for the third pulse and disappear from the fourth through the eighth pulses. The SEM images show that the ablated regions of the aluminum target surface melt and solidify after the irradiation of the femtosecond laser pulse. Some droplets are observed on the target surface in the SEM images. These demonstrate the occurrence of thermal effect in the process of the laser ablation in our experiments. Some micro- and nano-structures are also observed on the target surface after laser pulse ablation. Ablation by multiple femtosecond laser pulses differs from ablation by the single femtosecond laser pulse, and the differences are attributed to the changes to the surface structure of the aluminum target induced by the preceding multiple pulses. The results reveal the characteristics of the multiple femtosecond laser pulses ablation and may offer some guidance on the femtosecond laser material processing.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] |