† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11332006, 11732010, 11572221, and 11502066).
An experimental investigation was performed for active control of coherent structure bursting in the near-wall region of the turbulent boundary layer. By means of synchronous and asynchronous vibrations with double piezoelectric vibrators, the influence of periodic vibration of the double piezoelectric vibrators on the mean velocity profile, drag reduction rate, and coherent structure bursting is analyzed at Reθ = 2766. The case with 100 V/160 Hz-ASYN is superior to other conditions in the experiment and a relative drag reduction rate of 18.54% is exciting. Asynchronous vibration is more effective than synchronous vibration in drag reduction at the same voltage and frequency. In all controlled cases, coherent structures at large scales are regulated while the small-scale structures are stimulated. The fluctuating velocity increases significantly. A periodic regulating effect on the coherent structure can be seen in the ASYN control conditions at the frequency of 160 Hz.
High skin friction generated by wall-bounded turbulence, due to the higher energy consumption and the resulting environmental impact compared to laminar flow, makes the drag reduction technique in turbulence a dramatic topic not only in aeronautical and aerospace engineering, but also in many other industrial applications.[1–3] For wall-bounded turbulence control, a thorough understanding of the underlying physical mechanism of the wall-bounded turbulence and an efficient control technique are both indispensable.[4–10] Active control can adapt to changes in flowing conditions and realize optimal control.[11–19] Modern micro-electromechanical systems (MEMS) provide powerful tools for active control.[20,21] Among various active control schemes, wall deformation is a reliable and efficient solution. Grosjean et al.[22] tested the MEMS based pneumatic wall-deforming device, and found that the device was reliable even in transonic aircraft that experience great temperature variation. Cattafesta et al.[23] proposed the cantilever beam consisting of a piezoelectric ceramic sheet and a steel disc that were bonded together, and worked out the frequency response function of the piezoelectric vibrator by using an optimization algorithm. Segawa et al.[24] designed a set of devices that generated wall-normal vibration through an actuator array and effectively lowered the regularity of the banding structure in the near-wall region. Itoh et al.[25] used a loudspeaker to stimulate a polyethylene sheet on the wall and make it vibrate along the normal direction, thus realizing the drag reduction rate of 7.5%. Cattafesta et al.[26] made a summary of actuators used in various active control schemes, and pointed out that piezoelectric vibrators were one of the most important active control modes.
An active control scheme with double piezoelectric vibrators was employed in the present experiments. On the basis of the research with a single piezoelectric vibrator,[27–29] interference and regulation of multi-scale coherent structure bursts in a turbulent boundary layer were achieved by synchronous and asynchronous vibration of double piezoelectric vibrators respectively, which were embedded on the wall along the span-wise direction, and thus the drag reduction was achieved through different amplitudes and frequencies on the piezoelectric vibrators.
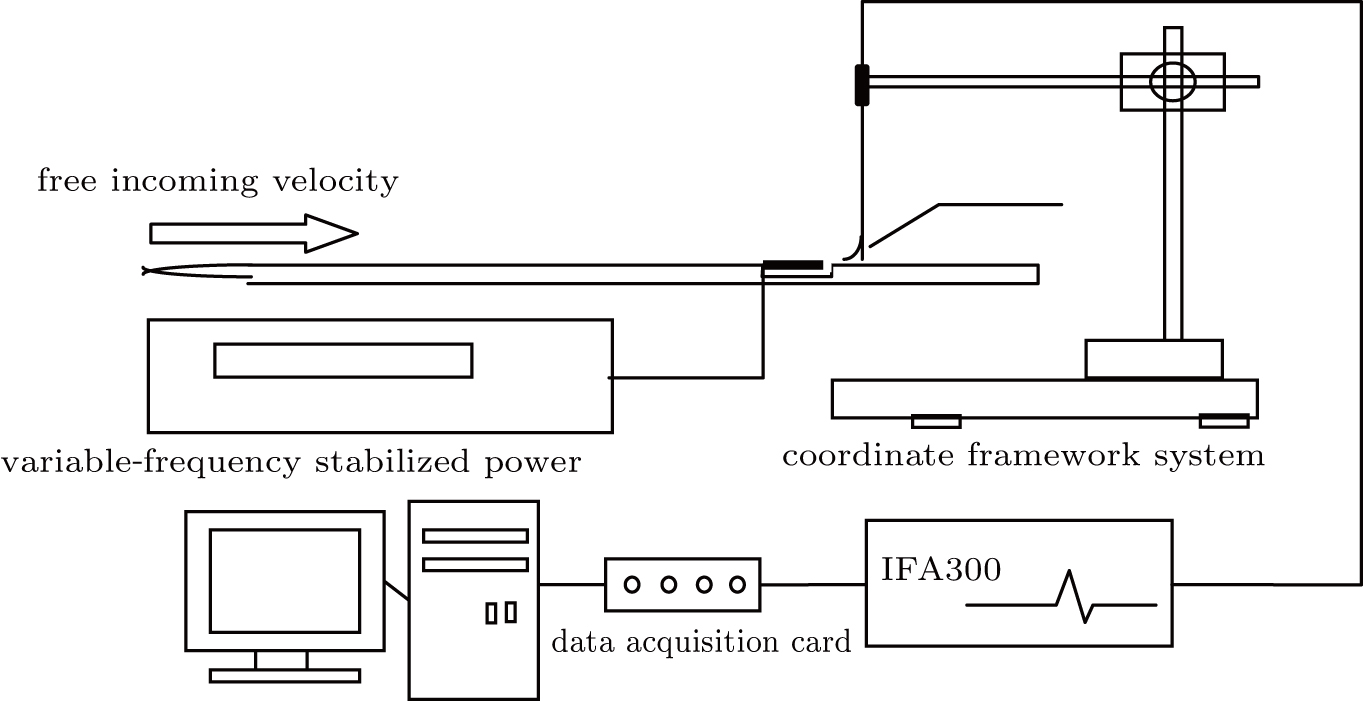
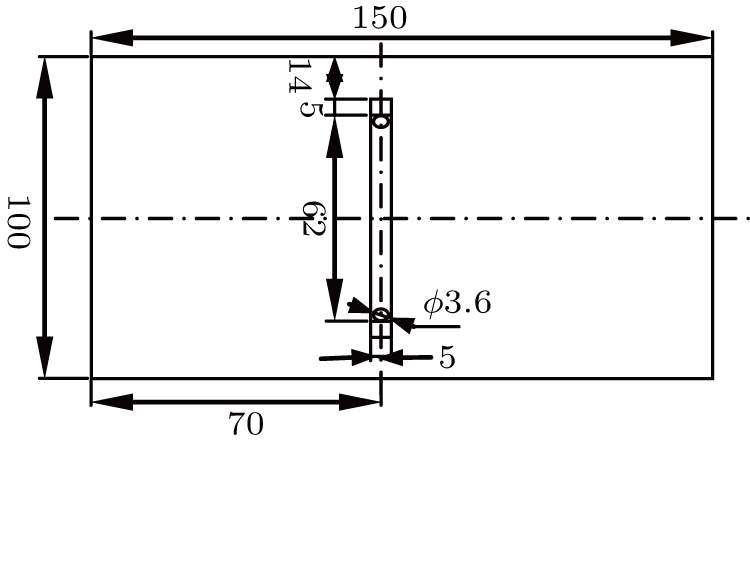
The experiment was carried out in a closed-circuit wind tunnel with a test section of 1500 mm (length) × 800 mm (width) × 600 mm (height). The zero-pressure gradient boundary layer flow was developing along a smooth flat plate of 15 mm × 600 mm × 1700 mm mounted on the center line vertically. The test plate was made of Plexiglas with a half-elliptical leading edge of a major to minor axis ratio of 16:1. A 2 mm diameter trip wire fixed downstream from the leading edge was used to develop the boundary layer on the test plate. The free-stream turbulence intensity was less than 0.2% owing to the use of porous plates, honeycombs, and mesh screens. On the center line 1090 mm away from the leading edge of the experimental plate, a 150 mm-long and 100 mm-wide cavity was made on the test plate at the location where the control actuators and measurement would be performed. Figure
The piezoelectric vibrators used in the experiment consisted of a 3.6 mm-wide and 0.2 mm-thick copper sheet and a 3.6 mm-wide and 0.22 mm-thick piezoelectric ceramic sheet that were bonded together. The effective vibrate length, thickness, and width of the oscillators were 30 mm, 0.42 mm, and 3.62 mm, respectively. Double piezoelectric vibrating plates were embedded in the groove along the span-wise direction (see Fig.
One wire was welded directly on the surface of the piezoelectric ceramic sheet and the other was welded on the copper sheet. When the two wires were connected to the AC power supply, the piezoelectric ceramic sheet would perform axial stretching vibration. The two wires were put through the small holes at the bottom of the cavity, placed at the backside of the plate, and connected to the AC power supply outside of the wind tunnel (see Figs.
The TSI-IFA300 hot-wire anemometer and TSI-1621 A-T1.5 hot-wire probe dedicated to measuring the boundary layer were used in the experiment. The sensitive hot-wire material was a tungsten filament 1.25 mm in length and 4 μm in diameter. The probe was calibrated using the TSI-1128 hot-wire probe calibrator. WIN-30DS4 12-bit A/D card, manufactured by the UEI company, was applied as the data acquisition card. The probe supporting rod was fixed on the CCTS-1193E 3-D automatic coordinate framework system. Table
| Table 1.
Basic fluid field of properties of the turbulent boundary layer. . |
The hot-wire probe was installed 2 mm downstream of the piezoelectric vibrators, and stream-wise velocity signals at different normal positions in the turbulent boundary layer were obtained. Different voltage amplitudes and vibrating frequencies of the piezoelectric vibrators were provided by the EVERFINE GK10005 AC variable-frequency stabilized power. Two voltage amplitudes (80 V and 100 V) and three vibrating frequencies (80 Hz, 160 Hz, and 240 Hz) were employed in this experiment. The electric power consumption was less than 0.1 W. Comparing the input power consumption to the drag reduction, the energy efficiency ratio (EER) was exciting.
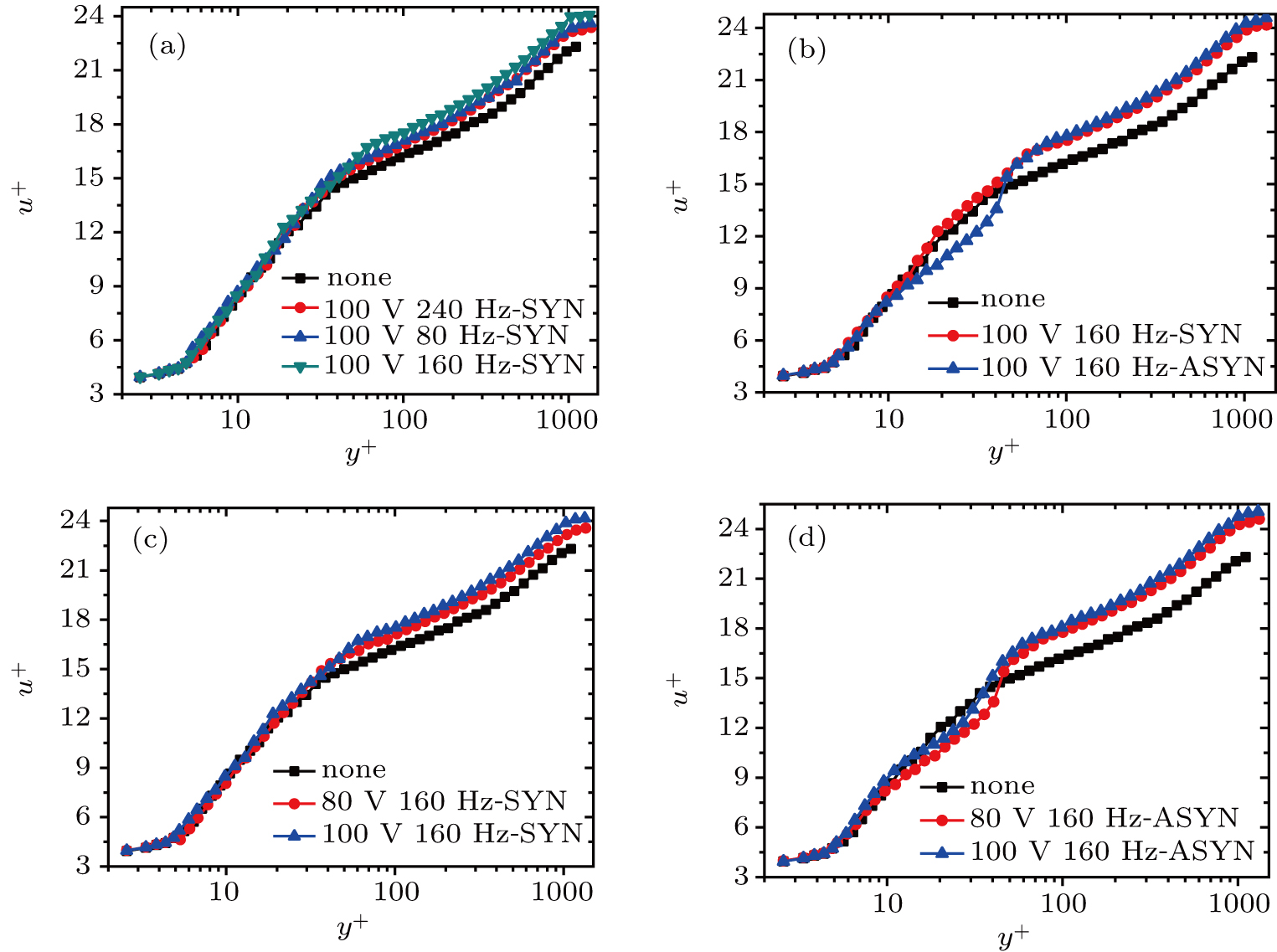
Figure
Figure
By using the wall friction velocity uτ, the wall shear stress can be obtained as
Table
| Table 2.
Wall friction velocity and drag reduction rate in various conditions. . |
Wavelet analysis is a mathematical method. It can be used to decompose a signal in both the time and frequency domains simultaneously by performing convolution on the signal and an analytic function called wavelet.[30–35] The wavelet coefficient Wu(a,b) of the one-dimensional velocity signal u(t) under the wavelet function Wab(t) is defined as
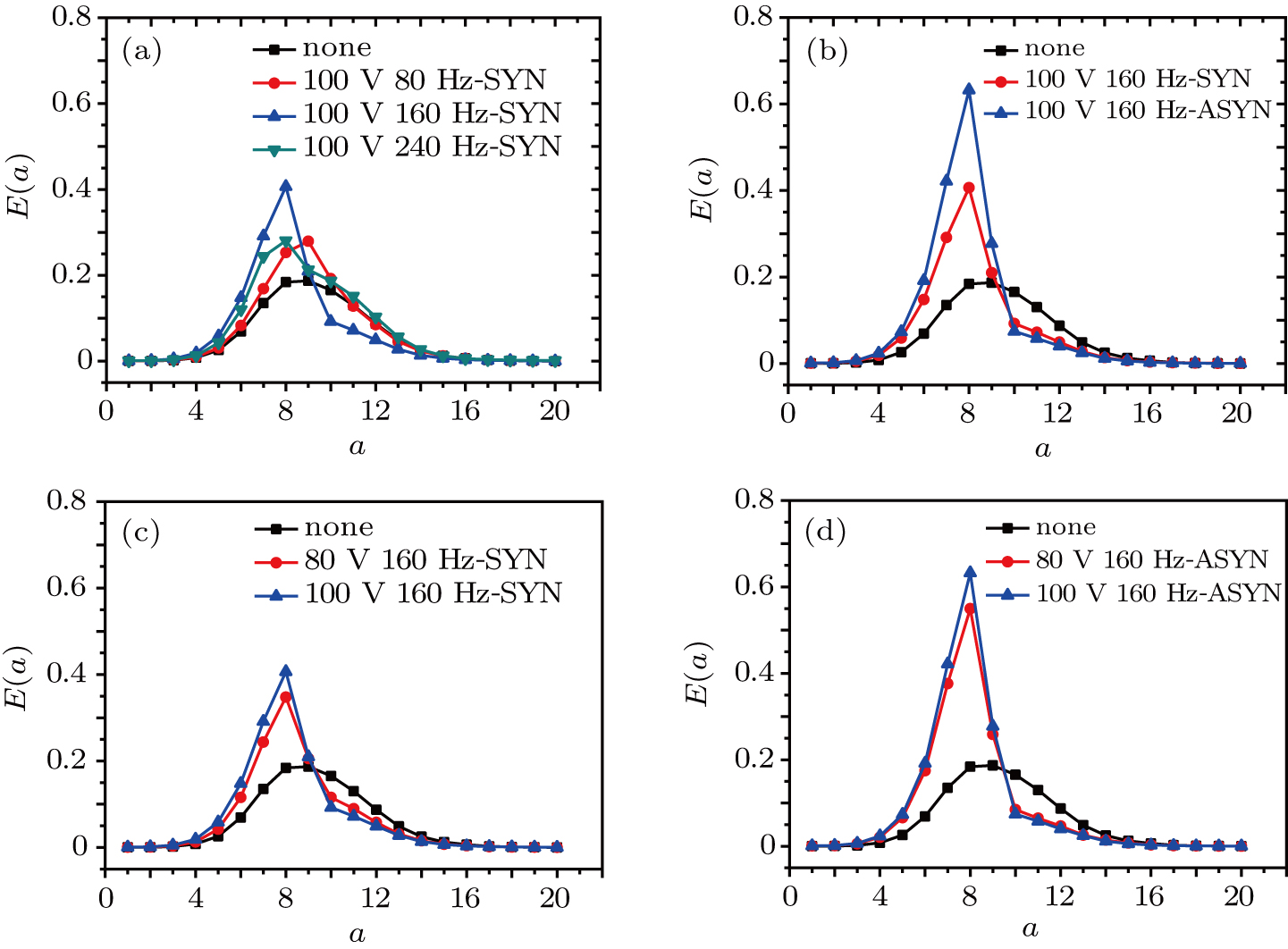
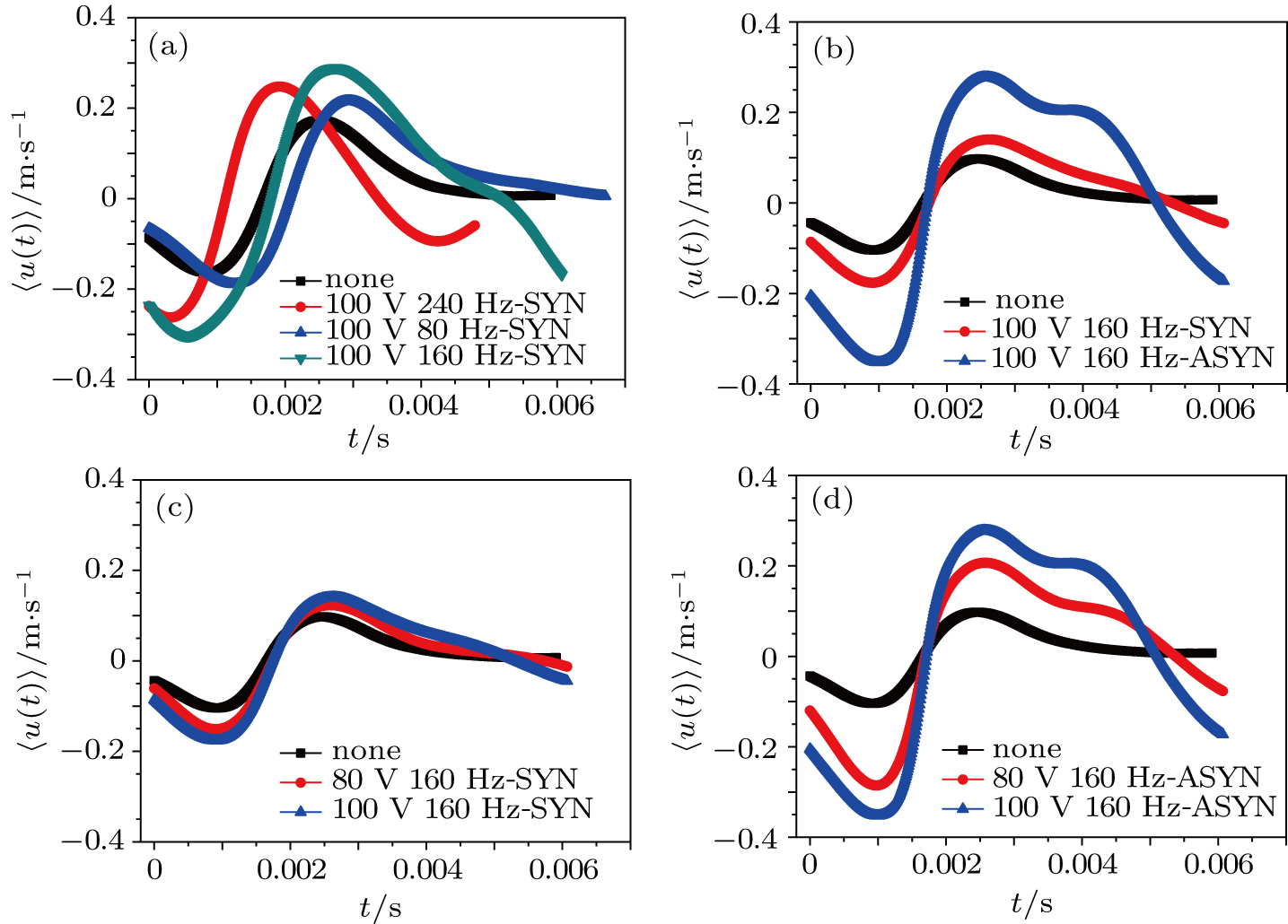
Figure
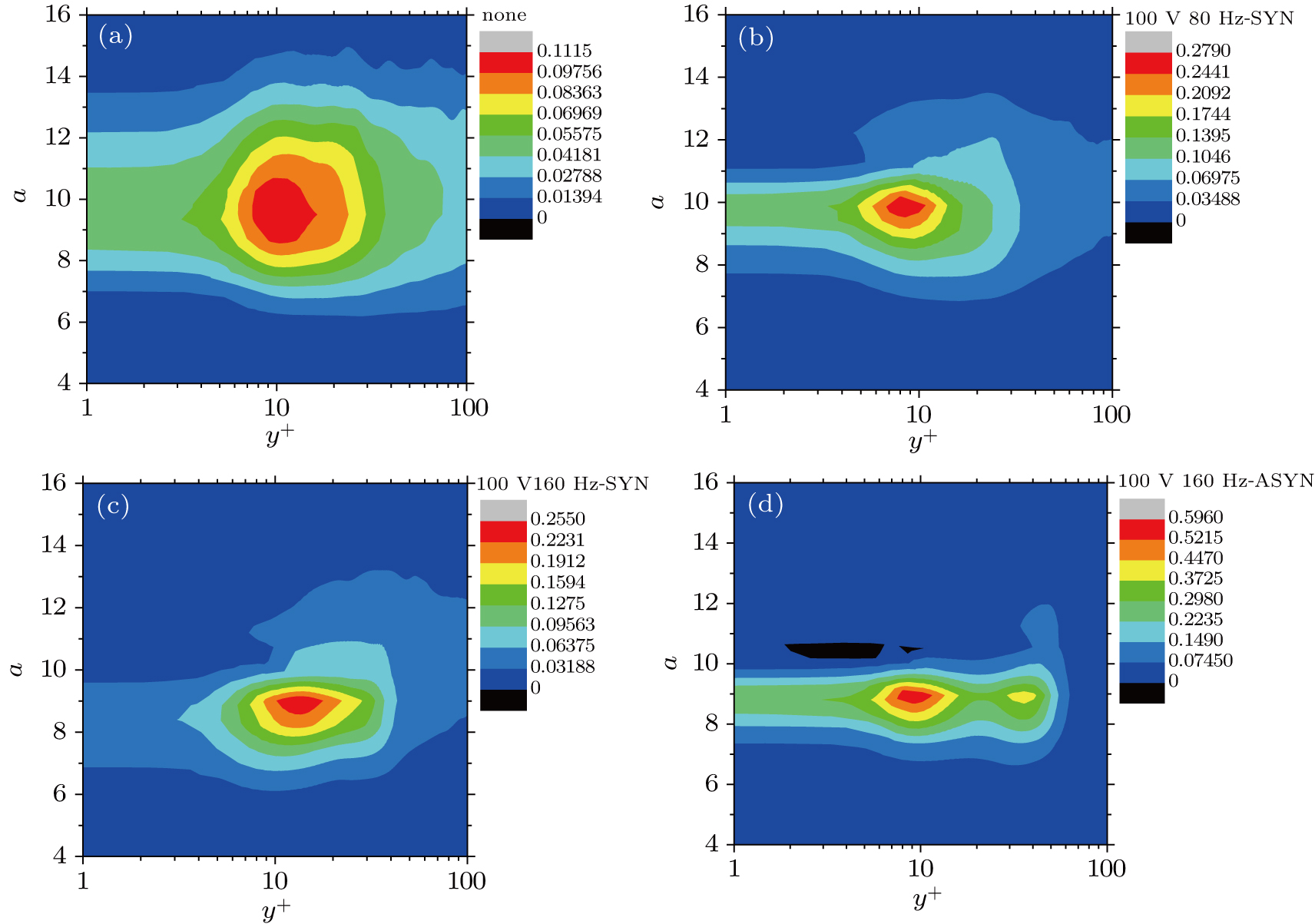
 | Fig. 5. (color online) Energy cloud distribution of the multi-scale flow structures: (a) none, (b) 100 V/160 Hz SYN, (c) 100 V/160 Hz SYN, (d) 100 V/160 Hz ASYN. |
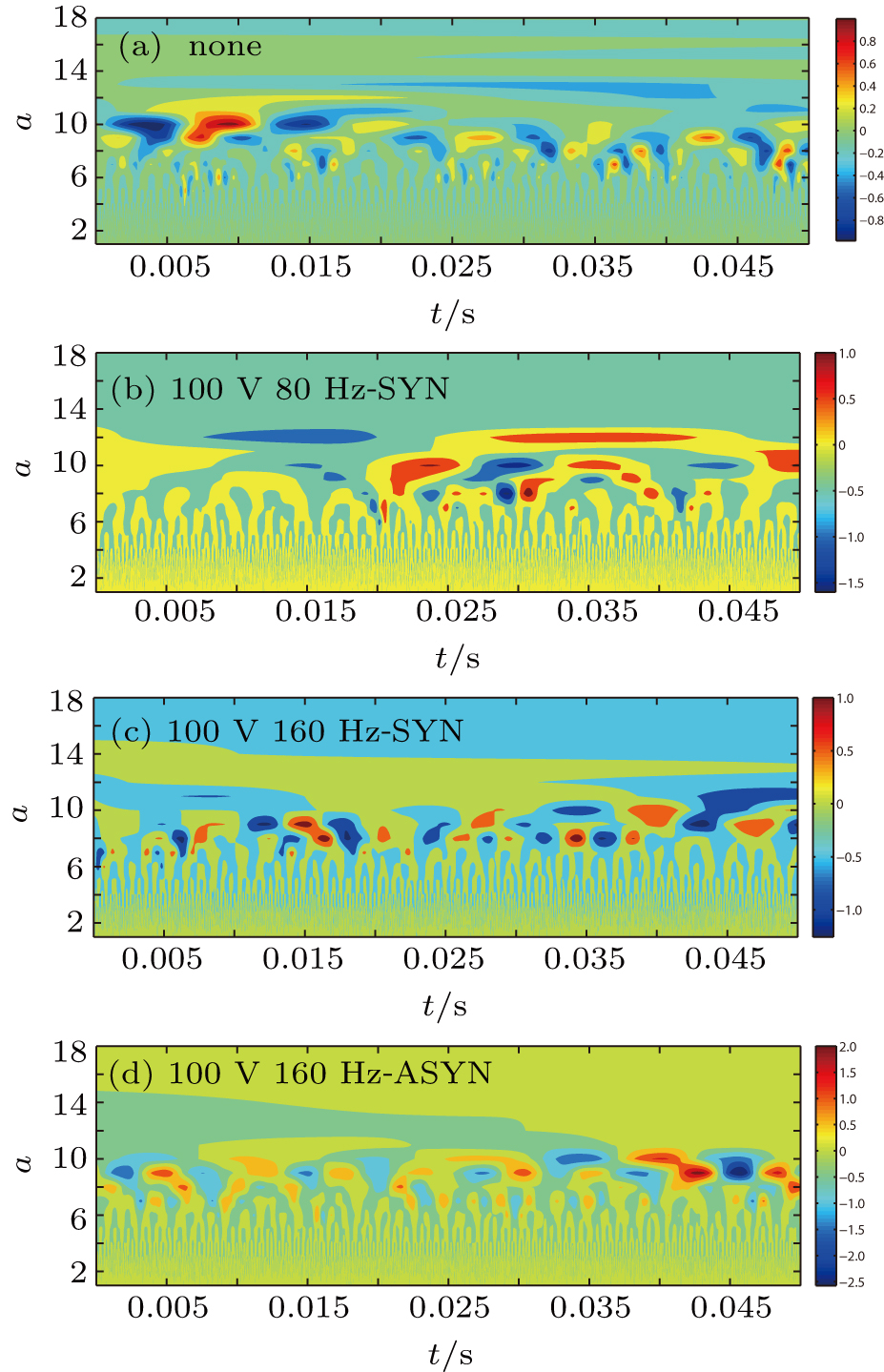
Figure
Periodic disturbances have a regulating effect on coherent structure bursting, resulting in the increase of energy at small scales and the decrease of energy at large scales. Namely, in the controlled conditions, turbulent dissipation increases, and less energy is generated.
Figure
 | Fig. 7. (color online) Energy cloud distribution of the multi-scale flow structures: (a) none, (b)100 V/80 Hz SYN, (c) 100 V/160 Hz SYN, (d) 100 V/160 Hz ASYN. |
In Fig.
As can be seen from Fig.
The influence of synchronous and asynchronous vibrations with the double piezoelectric vibrators on the turbulent boundary layer was analyzed from the aspects of average velocity profile, drag reduction rate, scale-dependent fluctuating energy distribution, and conditional phase-averaged waveforms of coherent structure bursting. The drag reduction rate can reach to the highest (18.54%) in the ASYN control case at 100 V/160 Hz. The effect of ASYN vibration is more obvious than that of SYN vibration. Higher voltage results in higher drag reduction rate in both SYN and ASYN conditions at the same vibrating frequency. When the vibrating frequency of the piezoelectric vibrators is close to the frequency corresponding to the energy-maximization scale of the coherent structure burst, the disturbances have the most obvious influence on the bursting and the higher drag reduction rate. Fluctuating velocity amplitude increases significantly in controlled conditions through the conditional phase-averaged waveforms. Maximum amplitude is observed in the 100 V/160 Hz-ASYN vibration condition, in which the best drag reduction effect is achieved. The periodic regulating effect on the coherent structure can be seen in the ASYN control conditions at the same frequency of 160 Hz.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] |