† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11501153, 11461018, and 11531003) and the Simons Foundation (Grant No. 523868).
We study the uncertainty relation in the product form of variances and obtain some new uncertainty relations with weight, which are shown to be tighter than those derived from the Cauchy–Schwarz inequality.
The uncertainty relations have played a fundamental role in the development of quantum theory not only in the foundation but also in recent investigations of quantum information and quantum communication, in particular in the areas such as entanglement detection,[1,2] security analysis of quantum key distribution in quantum cryptography,[3] quantum metrology, and quantum speed limit.[4–6] Usually the uncertainty relations are expressed in terms of the product of variances of the measurement results of two incompatible observables. Other forms of the uncertainty relations include entropic uncertainty principle,[7–9] variance-based sum uncertainty relation,[10–12] the skew information,[13,14] the majorization technique,[15–17] and the recent weighted uncertainty relation.[18] Recently, several experimental investigations were also performed to check the corresponding relations.[19,20]
In 1927, Heisenberg[21] analyzed the observation of an individual electron with photons and obtained the famous uncertainty principle
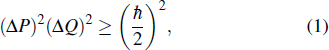 |
The inequality (
Robertson[22] formulated the uncertainty relation for arbitrary pair of non-commuting observables A and B (with bounded spectra) as follows:
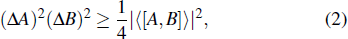 |
Robertson’s uncertainty relation was further generalized by Schrödinger to be[3]
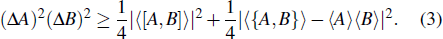 |
The goal of this note is to give a family of generalized Schrödinger uncertainty relations using a stronger Cauchy–Schwarz inequality.
We start with a quantum system in the quantum state ρ = |Ψ⟩⟨Ψ| on the Hilbert space with the inner product ⟨|⟩, where ⟨Ψ|Ψ⟩ = 1, and consider observables A and B. Define the operator 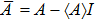
Let {|φi⟩} be an orthonormal basis of the Hilbert space and write 
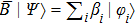
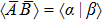
The variance of observable A can be expressed as 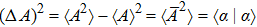
Until now we have considered only a pure state |Ψ⟩ of the system, this relation can be extended to the case of mixed states ρ = ∑pj|Ψj⟩⟨Ψj|, pj ≥ 0 and ∑j pj = 1. Since 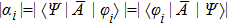
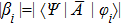
 |

Since the mean value of observable A can be expressed in the form of trace, ⟨Ψ|A|Ψ⟩ = TrA|Ψ⟩⟨Ψ|, we rewrite the inequality above as
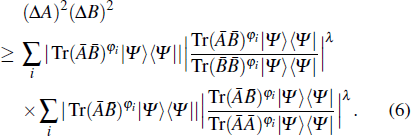 |
For each state |Ψj⟩, we have
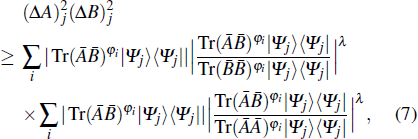 |
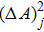

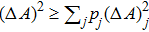
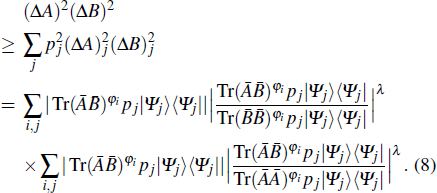 |
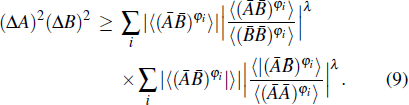 |
We remark that our generalized uncertainty relation is stronger than Schrödinger’s uncertainty relation, as the generalized Cauchy inequality shows that |⟨α|β⟩| is smaller than the right-hand side of our uncertainty relation.
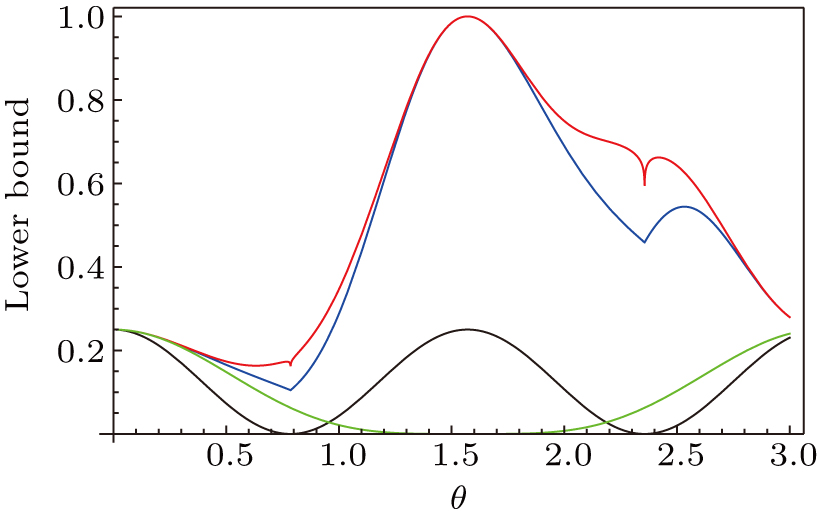
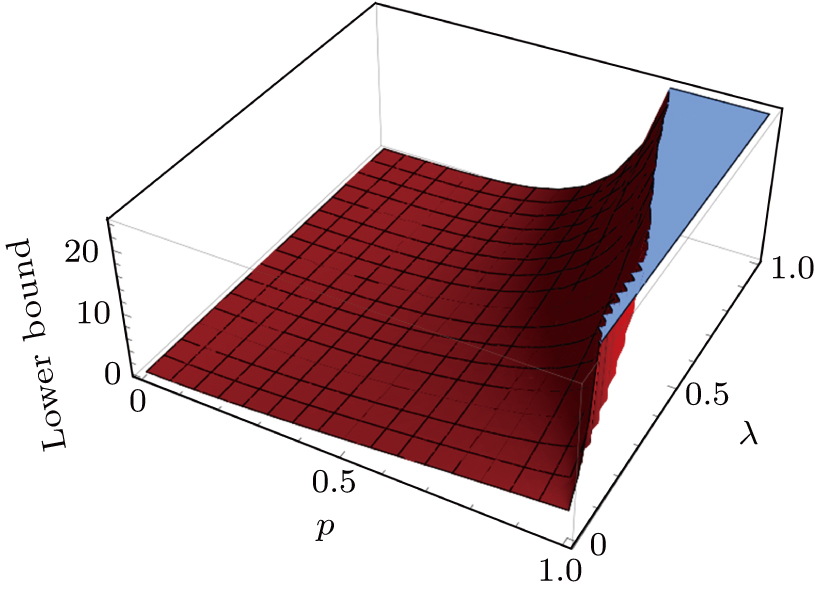
The uncertainty relation (
Both the Callebaut and Milne inequalities (
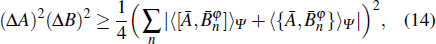 |
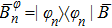
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] |