Project supported by the National Natural Science Foundation of China (Grant Nos. 61371009 and 61401282) and the National Key Scientific Instrument and Equipment Development Project of China (Grant No. 2014YQ030975).
Project supported by the National Natural Science Foundation of China (Grant Nos. 61371009 and 61401282) and the National Key Scientific Instrument and Equipment Development Project of China (Grant No. 2014YQ030975).
† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 61371009 and 61401282) and the National Key Scientific Instrument and Equipment Development Project of China (Grant No. 2014YQ030975).
In this paper, we present a compact quint-band superconducting filter operating at 2.4, 3.5, 4.7, 5.3, and 5.9 GHz. Matching junctions with different impedance branch lines are used to connect a dual-band sub-filter with a tri-band sub-filter and to reduce the channel interactions. The quint-band filter design is divided into two sections to determine the controllable frequencies and bandwidths, while ensuring compact size and reducing design complexity. The filter is fabricated on double-sided YBCO film deposited on an MgO substrate with a size of 26 mm × 19 mm. The measured results match well with the simulations.
Given the development of wireless communication systems, bandpass filters (BPFs) have aroused the increasing research interest of all.[1–3] Multi-band BPF is one of the most important front-end components. However, the addition of passband number leads to the increase of design difficulty and overall size. Few studies have reported quint-band BPFs or multi-band BPFs with more than five passbands.[4–7] In these studies, each BPF passband was generated by a single resonator or a pair of resonant modes, resulting in having only two or three poles on frequency response. Designing a high-order quint-band BPF with compact size, low insertion loss, and good selectivity is a great challenge.
Several methods of designing the multi-band BPFs have been developed and can be generally classified as three categories. The first category is to combine the BPFs, which have different resonant frequencies with common I/O ports. According to Ref. [8], the tri-band filter comprises three single-band sub-filters, in which each passband can be independently controlled. In a previous study,[9] two sets of resonators were employed to generate two dual-band responses, wherein these resonators are combined in parallel to achieve a quad-band filter. However, the overall size is large, especially for the designs with more than four passbands. The second category is to introduce the band-stop structures into a wideband BPF or transmission zeros (TZs) to a dual-band BPF to implement multi-band frequency responses.[10,11] This method has complicated design and fabrication with additional notch structures and is not suitable for widely spaced passbands. The third category is to use multi-mode resonators such as stepped-impedance resonators (SIRs),[12–14] stub-loaded resonators (SLRs),[15–17] and ring resonators.[18–20] Nevertheless, high-order filters are hard to construct because the internal and external couplings of all passbands are difficult to adjust simultaneously.
High-temperature superconducting (HTS) thin films with extremely low microwave surface resistance can be used to produce multi-pole single passband filters with both low insertion and sharp rejection. A few attempts have been made at superconducting filters with four or more passbands. In Ref. [21], the author proposed a quad-mode stub-loaded resonator and quad-feeding structures to design high-order quad-band HTS filters. A quad-mode square ring loaded resonator is used to implement a second-order quad-band HTS filter in Ref. [22]. These researches indicated that using multi-mode resonators can hardly adjust the resonant mode and the coupling of each passband independently, and are difficult to extend to high-order quint-band HTS filters.
In the present paper, a new design method which combines two different multi-band sub-filters into a quint-band BPF is proposed. A compact high-order superconducting quint-band filter is also presented. The first two passbands are constructed by four stub-loaded stepped-impedance resonators (SL-SIRs). The resonant characteristics are investigated and the harmonic frequencies are pushed upwards to prevent them interfering with the rest of the passbands. Moreover, three different types of resonators are combined to form a tri-band response, which corresponds to the last three passbands. A total of seven resonators are used to construct a wideband response, while two notch bands generated by two pairs of stub-loaded hairpin resonators are introduced. The two sub-filters are then integrated with a matching junction with branch lines of different widths to reduce the strong interactions between them. The filter is fabricated and measured. The simulated and measured results show good agreement with each other.
Figure
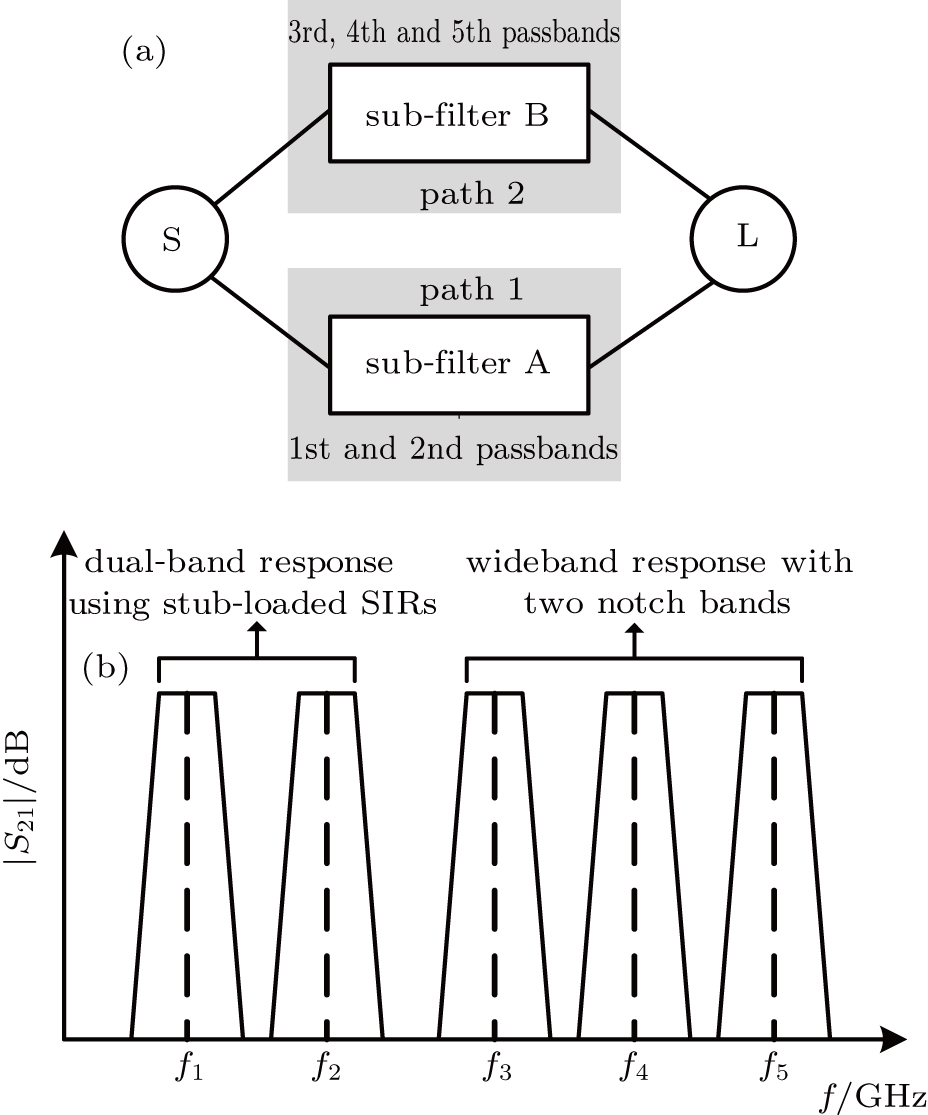 | Fig. 1. (a) Coupling scheme diagram of the proposed quint-band BPF. (b) Frequency response of quint-band BPF with five passbands contributed by two sub-filters. |
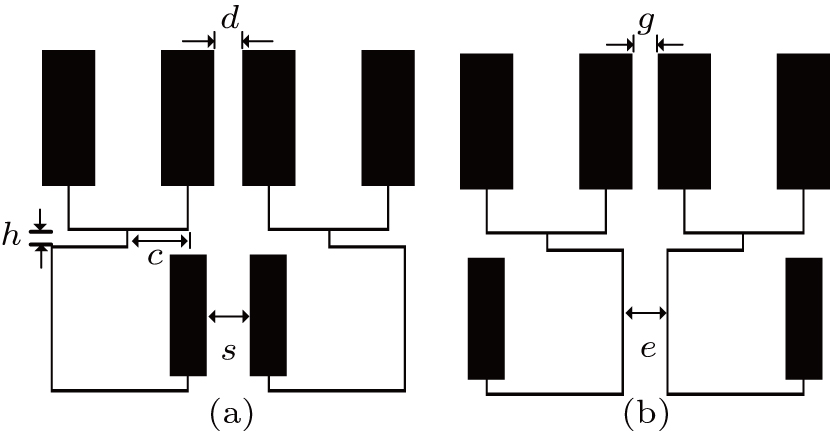
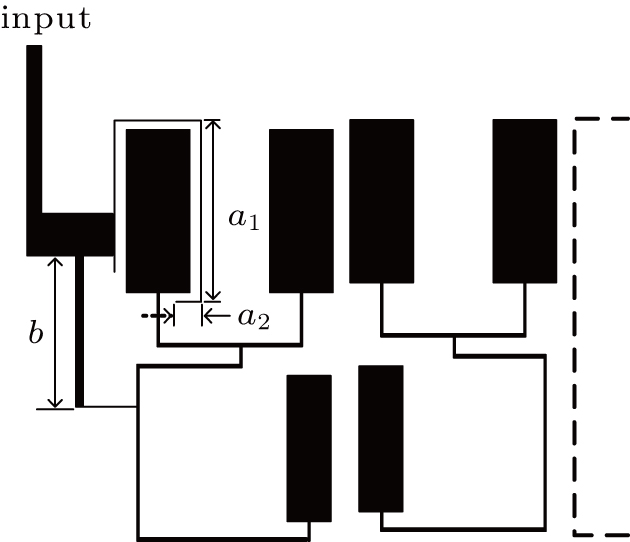
In the lower path of the quint-band filter, the first two passbands are constructed by four SL-SIRs. The simulated frequency responses, and current density distribution[23] of the SL-SIR are obtained and shown in Figs.
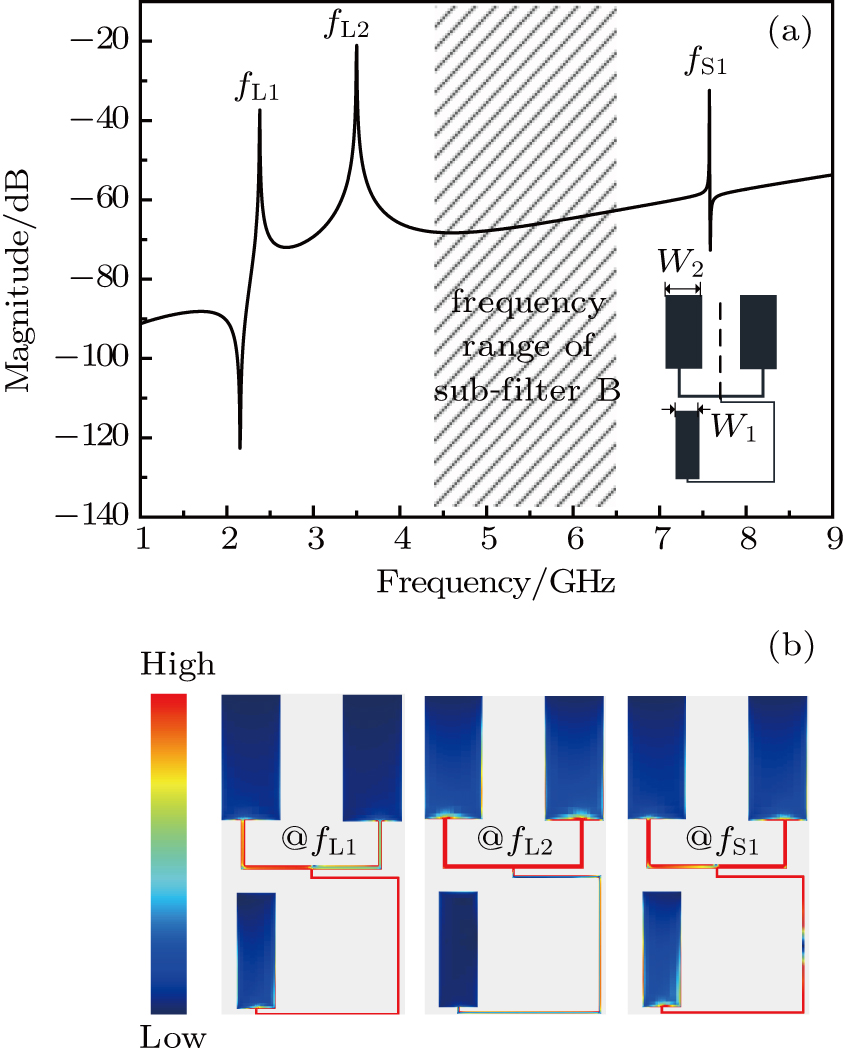 | Fig. 2. (color online) (a) Simulated resonant frequency response of the SL-SIR. (b) Simulated current density distribution of the SL-SIR at resonant frequencies of fL1, fL2, and fS1. |
The first two resonant modes generated by the SL-SIR are denoted as fL1 and fL2, and the first spurious frequency is represented by fS1. The current is distributed on the entire resonator at fL1, while it concentrates mainly on the upper part at fL2. Given that the open stub is shunted at the midpoint of the U-type SIR, the odd- and even-mode analysis can be adopted to characterize resonant modes. The lower frequency fL1 corresponds to the even mode, while fL2 corresponds to the odd mode.[24] Figures
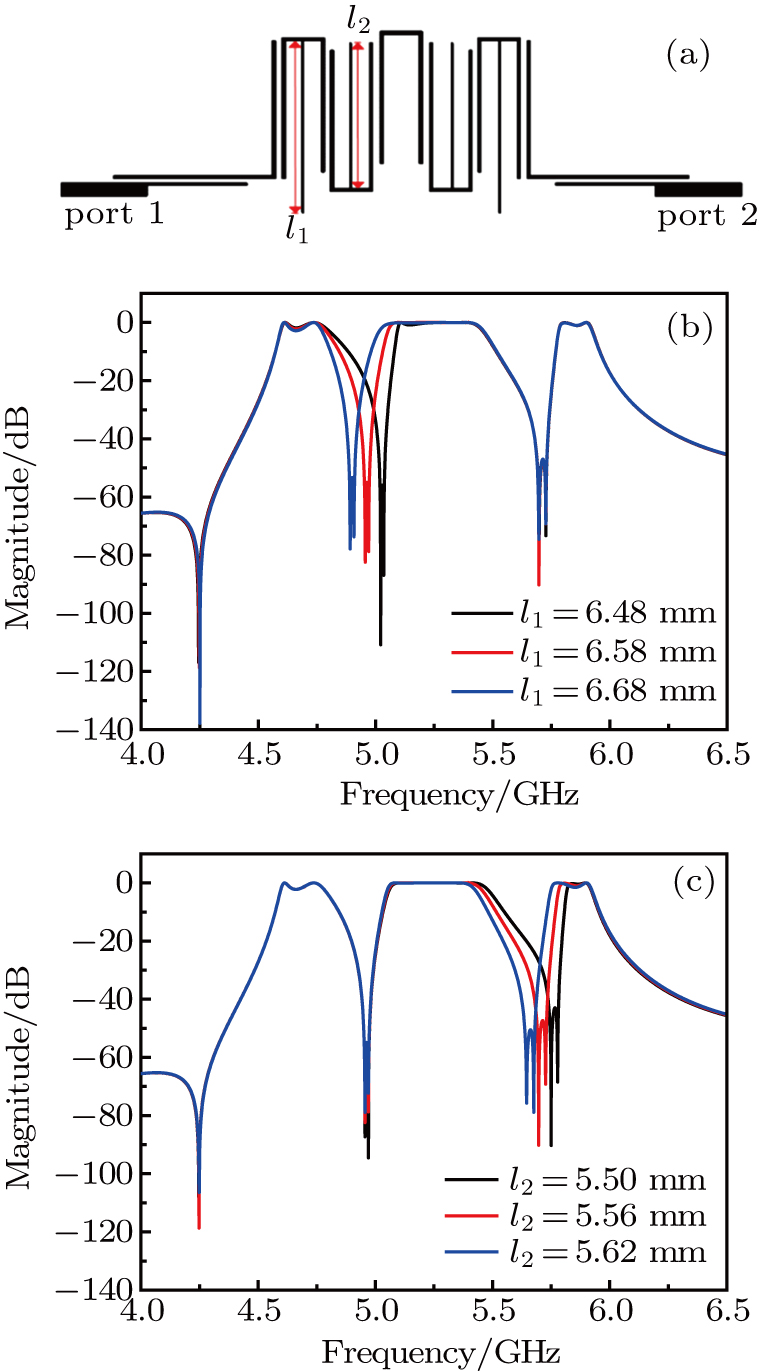
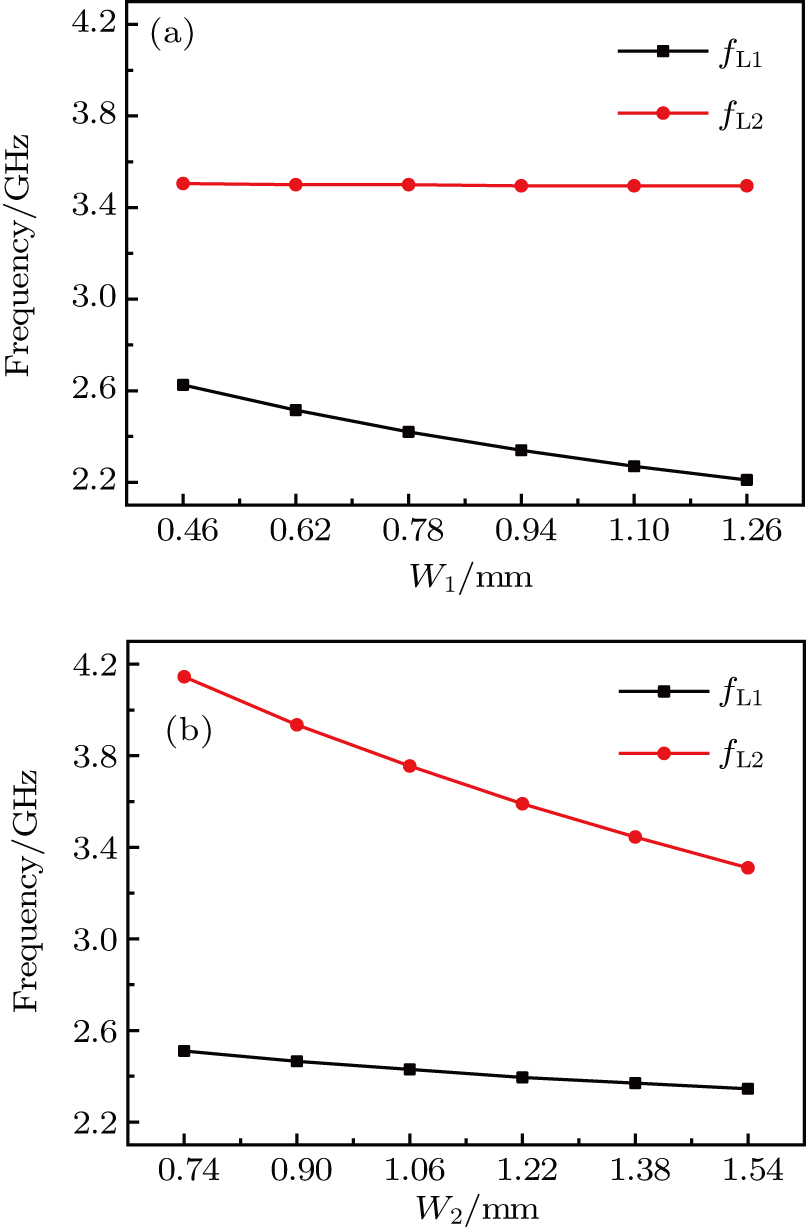 | Fig. 3. (color online) (a) Extracted resonant frequencies varying with W1 with W2 being set to be 1.32 mm. (b) Extracted resonant frequencies varying with W2 with W1 being set to be 0.86 mm. |
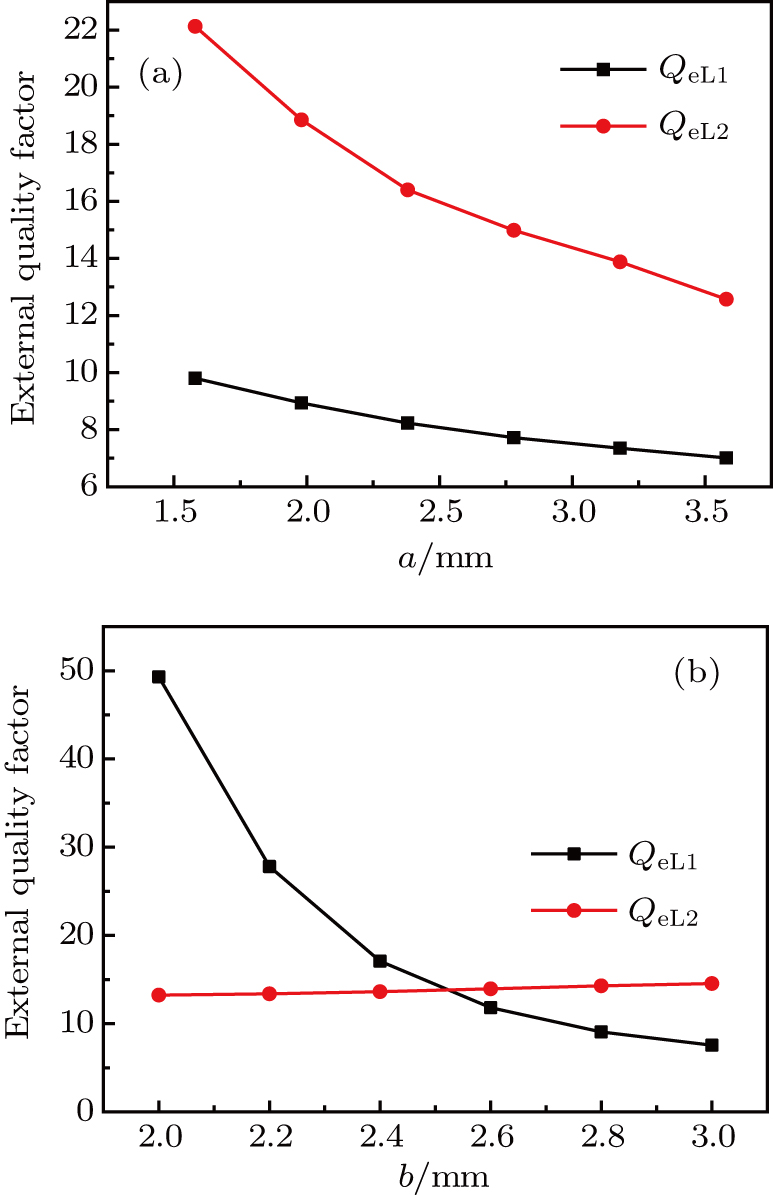
Figures
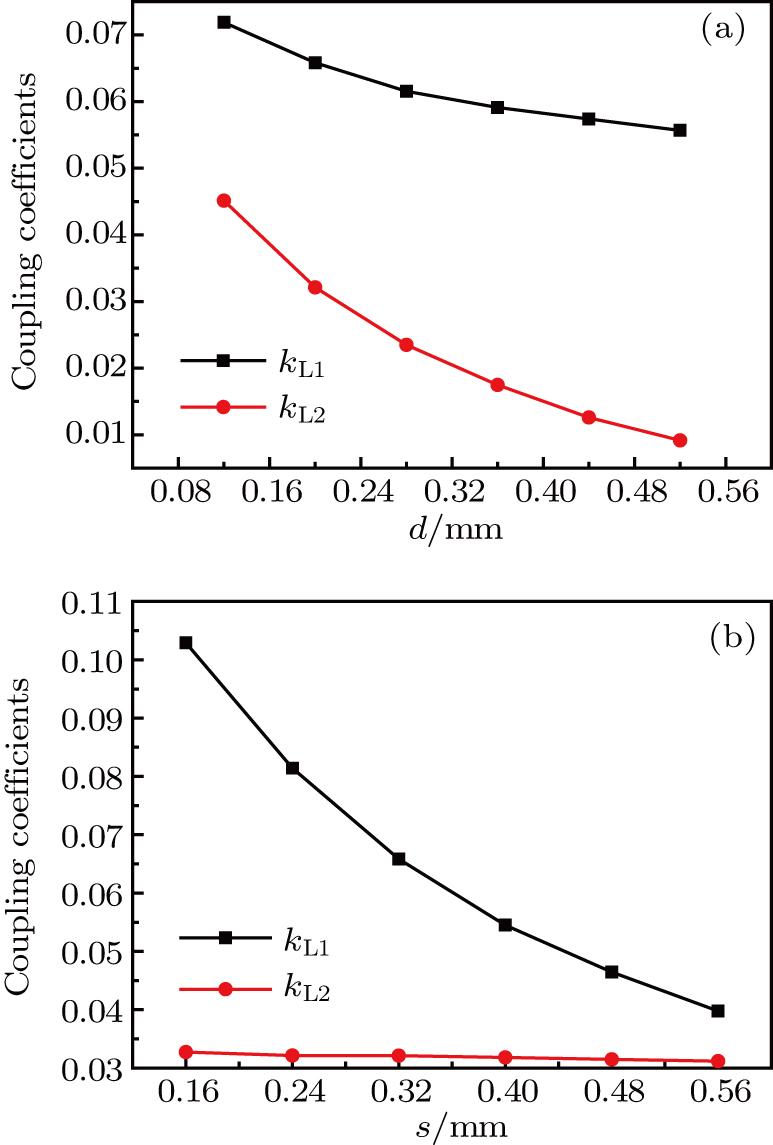 | Fig. 5. (color online) Simulated coupling coefficients in Fig. |
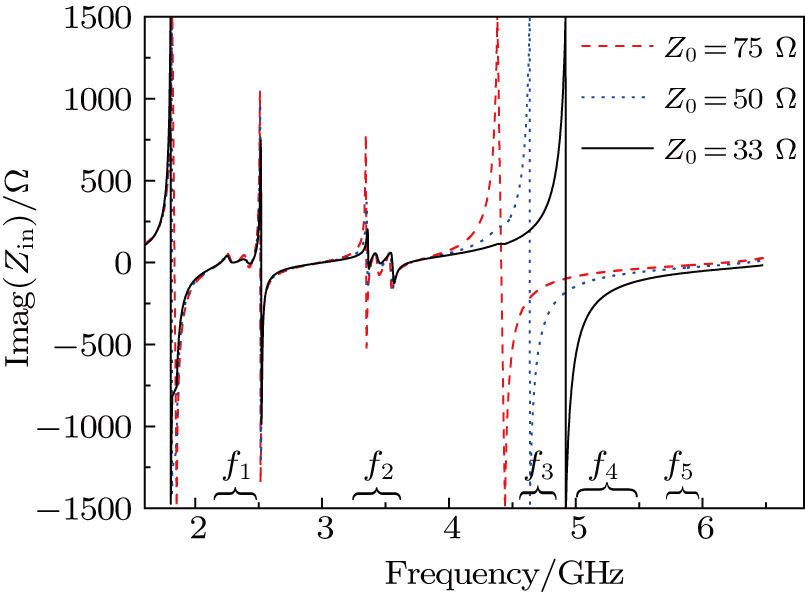
Figure
In the upper path of the quint-band filter, two notch bands are introduced into a wideband response. Seven resonators are used to construct the wideband response. The first and last resonator are transformed into L-type resonators to excite stronger external coupling to the ports, while the rest of the resonators are all hairpin resonators. The basic wideband response is shown in Fig.
Two pairs of stubs of different lengths are loaded in the middle of the hairpin resonators, introducing two notch bands as shown in Fig.
Figure
Figure
 |
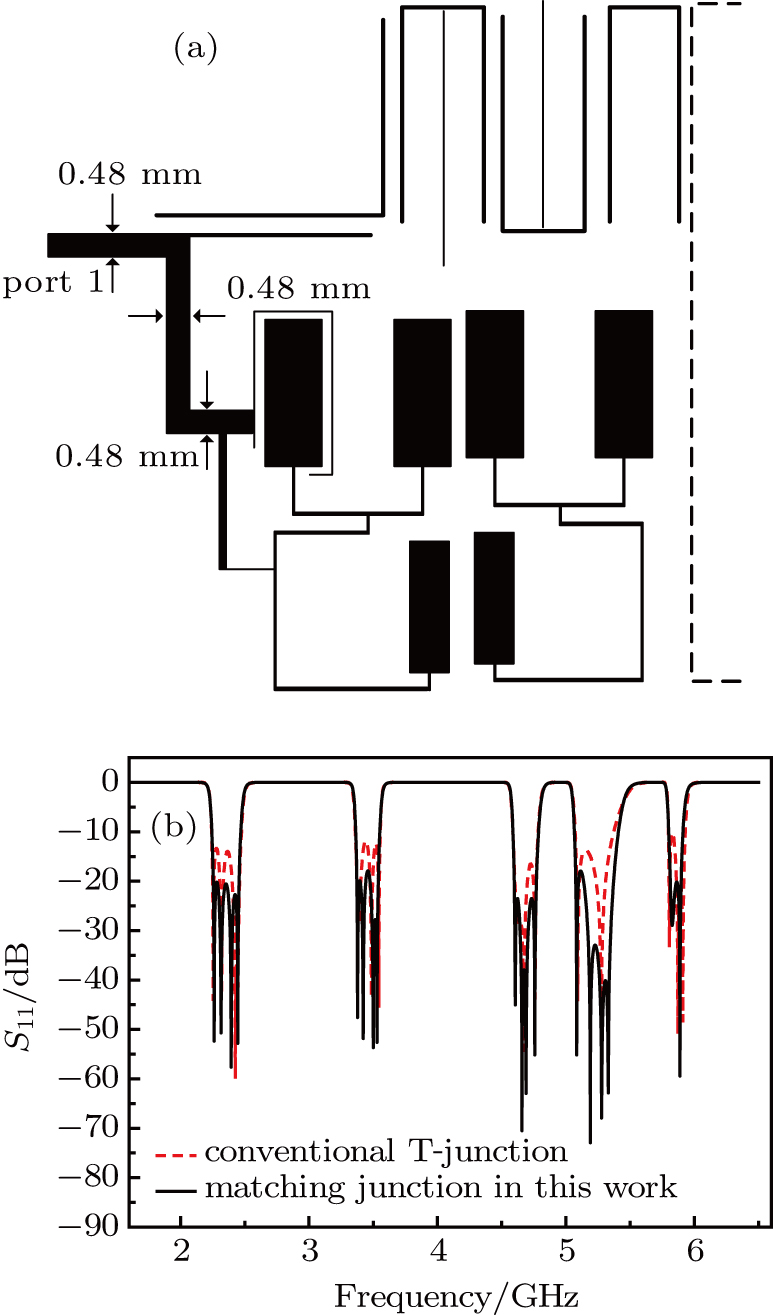
The two sub-filters are designed by adopting different structures of resonators, and the shortest distance between the two sub-filters is pulled away to 1 mm, so the cross-coupling can be weakened. Afterwards, the parameters of the quint-band filter, including the resonant frequencies, the external and interstage couplings, and the lengths of the matching branch lines, are optimized entirely to minimize further the undesired interactions and achieve a better filter response.
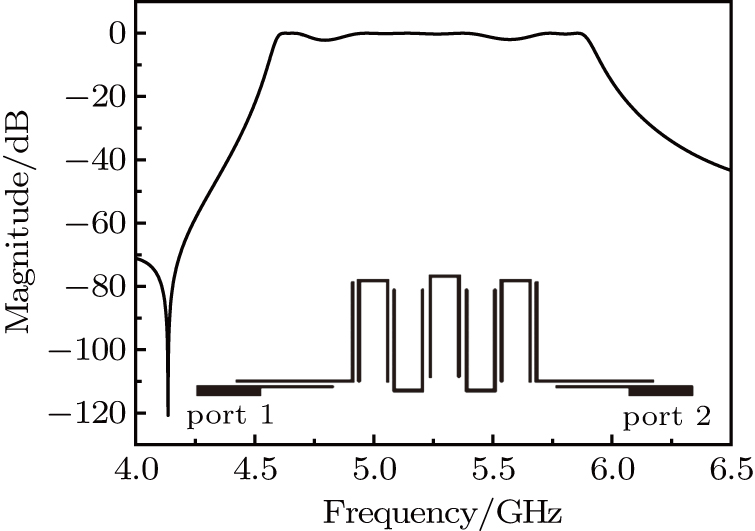
The quint-band HTS filter is fabricated on double-sided YBCO films deposited on a 0.5-mm-thick MgO substrate. The ion etching technology is used to etch one-side of the film to form the filter circuit. The filter is then packaged into a gold-plated shield box with an overall size of 26 mm × 19 mm, or 0.51λg × 0.37λg, where λg is the guided wavelength at the central frequency of the first passband. Figure
Figure
| Table 1. Measurements of the quint-band BPF. . |
Two high-pole multiband sub-filters have been constructed by adopting different structures and then used to determine a compact quint-band filter with controllable frequencies and bandwidths. The interaction between the sub-filters is reduced by the matching junctions with branch lines, which have different characteristic impedances. Experiments demonstrate that the designed and fabricated filter shows good return loss and low insertion, which matches well with the simulations.