Spectroscopic ellipsometry (SE) is a widely used technique to characterize surfaces, interfaces and multilayer structure non-destructively and non-invasively. It can offer precise measurements of optical constants of the materials over a wider wavelength range from the ultraviolet (UV) to the infrared (IR). Moreover, it has been used in the real-time monitoring of the fabrication of semiconductor devices. Basically, two independent parameters (Ψ and Δ) are used in SE measurement, compared with a single parameter of reflectivity in reflectometry. With the addition of tighter constraints, many material properties can be achieved via the ratio between these two parameters. This makes ellipsometry measurements insensitive to the fluctuation of light intensity, electronic drift, or scattered light loss. In addition, the phase quantity ‘Δ’ provides excellent sensitivity to the presence of very thin films.^[1]

The development of SE can be dated back to the 1880s.^[2,3] Drude first developed an ellipsometer in 1887 although this was not named an ellipsometer by him.^[4] Drude also proposed an elliptic equation, known as the Drude dispersion model that describes the optical constants of the metal and is still in use today. Most of the previous ellipsometers are based on the extinction light method with simple instrumental configuration. The drawback of the previous ellipsometers is that the measurement usually is involved in a large amount of data processing and complicated calculations, which takes a long time to collect all the data.^[5] Until the early 1970s, all the ellipsometers were still manually operated. In 1969, Cahan and Spanler first built an ellipsometer with an autorotation pick-up device.^[6] Muller and Farmer reported a spectral ellipsometer capable of on-line monitoring in 1974, which greatly increased the quantity of data collected.^[7] In the middle of the 1970s, Aspnes invented an ellipsometer in which the optical properties could be measured over a wider wavelength range by using a grating monochromator.^[7] Subsequently, a new era was dawning upon the application of modern SE. In 1977, Azzam and Bashara co-published the first textbook about SE.^[8] In 1990, the team from Pennsylvania State University developed a widely used online spectral ellipsometer.^[9] Due to the commercialization of spectral ellipses, the research based on ellipsometry dramatically increased. In the 1990s, SE was mainly used to characterize the thickness and optical properties of semiconductor materials. Nowadays, with the progress of the ellipsometer and the data analysis method, its application has been expanded from the initial field of semiconductor materials to that of biomaterials. Moreover, the composition of the feedback control can only be achieved using an ellipsometer. Therefore, it can be expected that the application of SE can be expanded to a wide range of materials in the future.

Our interest is to characterize the optical properties of chalcogenide glasses by using the SE. Chalcogenide glasses are the materials containing one or more chalcogen elements (S, Se, and Te) covalently bonded with other network forming elements such as Si, Ge, As, and Sb, etc.^[10] They have promise to be applied to photonics because they have attractive optical properties which include highly linear and nonlinear refractive indices, high photosensitivity, and exceptional transmission range spanning from the visible (vis) to the mid-infrared (MIR).^[11] For these purposes, it is essential to determine the optical constants of the glass like refractive index and optical bandgap. This is particularly important when the glasses are used as optical lenses, since optical design requires the exact values of the refractive indices. However, limited refractive index data of chalcogenide glasses are available in the literature,^[12–15] besides those of a few commercial compositions such as As₂Se₃, As₂S₃, Ge₂₈Sb₁₂Se₆₀, and Ge₃₃As₁₂Se₅₅. Especially, since the glasses are mostly used in the MIR region, it is a challenge that the refractive index in MIR is measured by using a traditional prism coupling method since not all the light sources are available. Instead, SE provides a solution to obtain the refractive index over a wide wavelength range. However, the linear refractive index data of the chalcogenide glasses are mainly concentrated in the visible and near-infrared (NIR) region, and there has been less research reported in the wavelength range of 2 μm and above. Therefore, it is urgent to establish a large optical database for chalcogenide glasses in MIR.

Two basic SE parameters ψ and Δ are defined as a complex ratio of the p-polarized Fresnel reflection coefficient (r_p) to the s-polarized Fresnel reflection coefficient (r_s), ρ, as follows:

Since the pseudo-dielectric function can be calculated, it is possible to obtain the refractive index n, the extinction coefficient k and the absorption coefficient α from the following equations:

A model is needed for analyzing the SE experimental data. Calculated model spectra are fit to the experimental data by varying model parameters, which factorizes the optical function spectra of interest.^[16] Therefore, the correct physical structure and dispersion relation are important to obtain the better simulation results for the measurement results.

Regarding the physical structure of the sample, calculated SE parameters can match the measured ones if the physical structure model is close to the real structure of the sample. For the study of chalcogenide bulk glasses in the broad spectral region, a physical structure with double layers is chosen, i.e., a surface rough layer and a bulk material. For the calculation of microscopic surface roughness, an effective medium model is usually used in SE. If an appropriate parameterization of the optical function, i.e., model dielectric function, is available for the materials of interest, the number of unknown parameters for data analysis can be greatly reduced.

The data analysis is a little complicated for thin films, especially for those films with multilayers. In a multilayer structure model including substrate and dispersive layer, defining the optical response of underlying layers is very important. It can not only reduce optical correlation effects between layers, but also obtain more accurate values for the thickness of the top layer and the optical constants.

Regarding the dispersion model, a lot of different dispersion relationships have been applied to the analysis of VASE data, such as Gaussian (G), Tauc–Lorentz (TL), Cody–Lorentz (CL), Sellmeier, Cauchy, Drude models, etc. For example, it is well known that the dielectric function 〈ε〉 substantially relates to the energy band structure and optical parameters for phase change materials. In the phase change process, the structure variations could lead to the significant difference in optical constant. The Gaussian model was used to fit the dielectric function 〈ε〉 of the experimental data in this case.^[17] It ensures the Kramer–Kronig consistency of the real and imaginary parts of a complex-valued dielectric function. The G model was found to be extremely effective to simulate the optical properties of the material in IR relating to molecular or lattice vibrations.

The TL model, which is a multiplication of the Tauc and Lorentz models, has been widely applied to the description of optical responses in amorphous semiconductors or dielectric materials. However, the weak Urbach absorption and localized state are ignored in the TL mode. Therefore, when the photon energy is lower than the optical bandgap of the material, the imaginary part of the dielectric function ε₂ is limited to zero in the TL model. This is in contrast to the fact of non-zero dielectric function ε₂ below the optical bandgap due to the effect of the defects and interband absorption (Ref. [18]). The TL model works reasonably well to fit optical constants of crystalline materials in the UV spectral region and the chalcogenide glasses in the vis-to-NIR spectral region.

The CL model including both the correct band edge function and weak Urbach absorption tail was demonstrated to be more appropriate for the description of the optical functions in amorphous chalcogenide thin films. For detailed information about the principal of the CL model, see Refs. [19] and [20].

The Sellmeier and Cauchy models^[21] are also widely used in chalcogenide glasses, which are given in Eqs. (6) and (7), respectively:

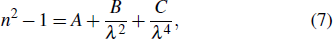As indicated in Eq. (6), the Sellmeier model contains a number of terms in the right part. Since the second term on the right-hand side of Eq. (6) becomes infinite as λ → a_n, the Sellmeier model can only be applied to the non-absorbing spectral region of the material. The Sellmeier model is non-analytical, and thus the corresponding imaginary part of the refractive index relating to loss cannot be achieved by using this model. On the other hand, the Cauchy model, which is not consistent with the Kramers–Kroning model, is an empirical relationship for normal dispersion. In other words, it relates the refractive index to the wavelength with parameters which have no physical meaning.

For the semiconductor material with a low resistivity and thus more free carriers, the Drude model is usually used in the IR region of 0.1 eV–0.6 eV (amorphous and crystalline) and the UV-vis region of 0.6 eV–4.13 eV (crystalline).^[22]

Obviously, each dispersion relationship has its own scope of application. For a material whose physical properties are not clearly known, usually a number of experiments to try a different dispersion relationship are necessary since it is not easy to find a single dispersion relationship that can fit the optical constants in a wide wavelength range. Moreover, a combination of the different dispersion relationships has been demonstrated to be extremely useful for simulating the experimental data.

A regression analysis is used to differentiate the model parameters until the calculated data are matching with the measured ones as closely as possible. This is performed by minimizing the mean square error (MSE) function, which is appropriately weighted to the estimated experimental errors.^[16]

Němec et al.^[23] measured linear refractive index of chalcogenide glasses (As₂Se₃ and Ge₂₈Sb₁₂Se₆₀) by using SE (J A Woollam Co., Inc.). The measured spectral range was from 1700 nm to 2.0×10⁴ nm (NIR-MIR) in steps of 20 nm, and the angles of incidence were 50°, 60°, and 70°, respectively. To derive refractive indices in the NIR-MIR spectral range, a Cauchy-like dispersion relation was adopted where the extinction coefficient in the first approximation was set to be zero. The curves in Fig. 1 represent the refractive indices determined by VASE for As₂ S₃ and Ge₂₈Sb₁₂Se₆₀ bulk glasses while the cross dots in Fig. 1 show the excellent agreement between the experimental data measured by VASE and the prism coupling method for two commercial selenide glasses, which validates the reliability of infrared SE.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Curves of refractive index dispersion of bulk As2Se3 (full curves) and Ge28Sb12Se60 (dashed curves) glasses determined by SE. Cross dots represent the data published by the commercial producers. The inset shows 900 nm–14000 nm spectral range in detail (Copyright by Němec et al. (2013).[23]

For the chalcogenide glasses and other semiconductor materials,^[24] a TL model has been used to fit the complex refractive index in the vis-to-NIR spectral region. However, because of the piecewise nature of the TL model, its general implementation in time-domain-type numerical modeling has proved impractical.^[25] Material dispersion may be obtained from the second derivatives of Eqs. (6) and (7). Nevertheless, the Cauchy model in this form does not encompass the entire glass transparent window. Instead, in representing the real part of the refractive index, for which the extinction coefficient is negligible,^[25,26] the Sellmeier model has been shown to be accurate for As–(Ge)–Se glass compositions. The As–(Ge)–Se chalcogenide glasses were modeled accurately only up to 2.3 μm in Ref. [26] by using the first Sellmeier term and a constant in Eq. (6). However, the wavelength range of the refractive index measurement data available is not enough in Ref. [26] to model the material zero dispersion wavelength, since this generally requires the refractive index in a wavelength range up to more than 10 μm. Seddon et al.^[21] measured the refractive indices of two As–(Ge)–Se chalcogenide glasses in a wavelength range from 0.4 μm to 33 μm, and they verified that the Sellmeier model including the second term in Eq. (6) is enough to obtain the accurate dispersion of the refractive index dispersion across their transparent window.

Wang et al. (2017)^[27] measured the refractive indices and thermo-optic coefficients of Ge₁₄As_xSe_86−x (x = 4, 8, 12, 16, 20, 23.2, 28, 32) and Ge_xAs₁₂Se_88−x (x = 17, 21, 23.3, 25, 27.5, 29, 33) glasses in the 2 μm–12 μm mid-infrared range, but detailed information regarding the fitting model was not mentioned in the paper. They found that the density shows a maximum at the stoichiometric composition or 〈r〉 = 2.512 (the mean coordination number) when the Ge content is fixed at 14%; while it exhibits a minimum at 〈r〉 = 2.67 when the As concentration is fixed at 12%. The refractive index and the thermo-optic coefficient of a Ge–As–Se glass could be predicted with an error of < 1% and < 6 ppm/K, respectively. The measured wavelength-dependent refractive indices at 25 °C for the Ge–As–Se glasses are summarized in Table 1. From the table, it can be found that the refractive indices decrease with wavelength increasing. This is in agreement with the refractive index dispersion of the optical glasses in their transparent windows.

Table 1.

Table 1.

Table 1. Measured refractive indices at 2, 4, 6, 8, 10, and 12 μm at 25 °C for Ge–As–Se glasses (Copyright by Wang et al. 2017).[27] . Composition 2 μm 4 μm 6 μm 8 μm 10 μm 12 μm Ge14As4Se82 2.4747 2.4585 2.4540 2.4504 2.4461 2.4415 Ge14As8Se78 2.4976 2.4834 2.4794 2.4761 2.4722 2.4679 Ge14As12Se74 2.5204 2.5034 2.4984 2.4942 2.4891 2.4838 Ge14As16Se70 2.5492 2.5337 2.5288 2.5246 2.5194 2.5135 Ge14As20Se66 2.5845 2.5668 2.5614 2.5568 2.5510 2.5448 Ge14As23.2Se62.8 2.6026 2.5801 2.5737 2.5686 2.5628 2.5560 Ge14As28Se58 2.6005 2.5769 2.5702 2.5650 2.5588 2.5521 Ge14As32Se54 2.6127 2.5919 2.5862 2.5816 2.5761 2.5705 Ge33As12Se55 2.5398 2.5173 2.5107 2.5054 2.4991 2.4918 Ge29As12Se59 2.4852 2.466 2.4600 2.4546 2.4482 2.4408 Ge27.5As12Se60.5 2.4756 2.4537 2.4470 2.4413 2.4346 2.4267 Ge25As12Se63 2.4732 2.4525 2.4462 2.4408 2.4347 2.4270 Ge23.3As12Se64.7 2.4901 2.4694 2.4630 2.4573 2.4506 2.4428 Ge21As12Se67 2.4962 2.4791 2.4736 2.4687 2.4628 2.4557 Ge17As12Se71 2.5200 2.5038 2.4988 2.4945 2.4895 2.4836

Table 1. Measured refractive indices at 2, 4, 6, 8, 10, and 12 μm at 25 °C for Ge–As–Se glasses (Copyright by Wang et al. 2017).[27] .

Synowicki and Tiwald (2004)^[28] employed the combination of multi-Gaussian–Lorentz and TL to fit the optical properties of As₂S₃ glass. The real and imaginary parts of the dielectric constants in As₂S₃ bulk glasses are shown in Fig. 2. Excellent agreement between the experimental data and the fitting results with a combination of two TL and four smaller G oscillator functions demonstrates that the combination of various dispersion relationships provides a flexible way to fit the optical constants, meanwhile the Kramer–Kronig consistency can be kept in a wide wavelength range.

Fig. 2.

	Figure Option ViewDownloadNew Window
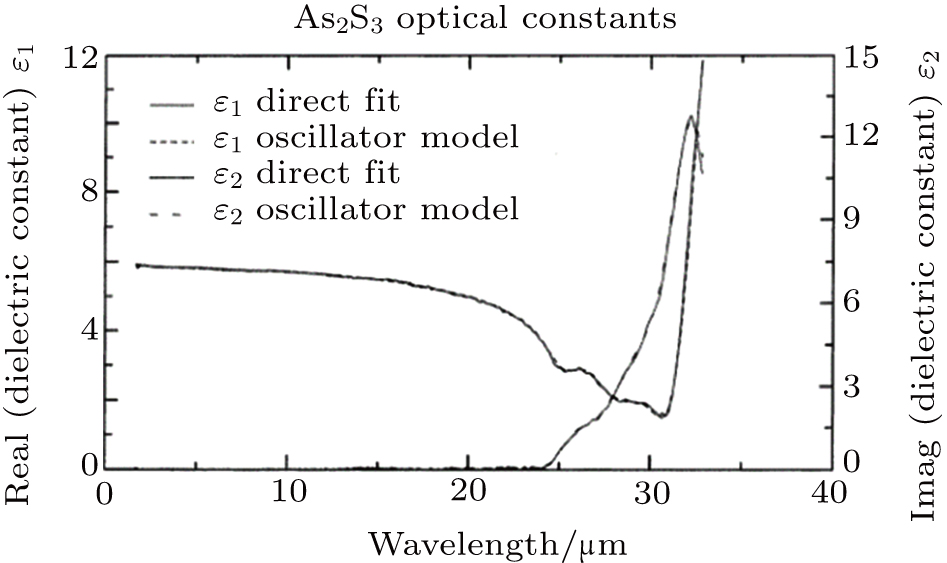	Fig. 2. Plots of a-As2 S3 optical constant versus wavelength in a range of 1.7 μm–33 μm. Four G models were used to fit the optical constants (Copyright by Synowicki and Tiwald 2004).[28]

There are also some tricks to obtain the reliable experimental results. The surface roughness has to be small enough, and the incident light has to be oblique. If the surface of the sample is rough, part of the incident light would be scattered away, so that the intensity of the light received by the detector decreases greatly. The sample should be polished on one side, uniform in thickness, and free of scratches, bubbles and defects. If both side surfaces of the sample are not parallel to each other, the light path of the quad-detector alignment window of VASE will be out of alignment, the measurement result certainly is not ideal. Of course, the size of the sample should also be bigger than that of the beam. In this case, the light beam can be focused on the sample completely during the measurement. Finally, SE measurements should be performed at oblique angles near the Brewster condition. This provides the highest sensitivity to material properties, such as refractive index and film thickness. The Brewster conditions of samples are different from each other and also change over the spectral range. Thus, a variable angle of incidence allows the measurement to be optimized for each data point.

Basically, a high quality of the sample, reasonable physical model and material dispersion relationship are essential to achieving better results. Table 2 shows recent measurements of the optical constants in chalcogenide glasses by using different models in different spectral ranges.

Table 2.

Table 2.

Table 2. Recent applications of the SE in chalcogenide glasses. . Component Model Spectral range Angle Physical structure model Dispersion relationship Ref. Ge–As–Se IR-VASE, J A Woollam, Lincoln, NE 1 μm–13 μm – – – [27] Ge–As–Te VASE, J A Woollam, Co., Inc., Lincoln, NE 0.3 μm–20 μm 50°, 60°, 70° Cauchy CL model, Sellmeier model [29] As40Se60/Ge10As23.4Se66.6 VASE, J. A. Woollam, Lincoln, NE 0.4 μm–33 μm 55°, 75° – Sellmeier model [21] As2Se3/Ge28Sb12Se60 VASE/IR-VASE 0.3 μm–2.3 μm/1.7 μm–20 μm 50°, 60°, 70° Cauchy CL model [23] As33 S67−xSex VASE® J A Woollam Co., Inc. 0.3 μm–2.3 μm 60°, 65°, 70° Cauchy TL model [30]

Table 2. Recent applications of the SE in chalcogenide glasses. .

It is obvious from Table 2 that the refractive index data of the chalcogenide bulk glasses that can be obtained in the literature are limited, mostly involved in some commercially available compositions. Therefore, it is urgent to have a full set of the database regarding the refractive indices of chalcogenide glasses with various compositions in a wider wavelength range in order to meet the requirements for optical design of infrared lens.

Nemec et al. (2008)^[31] explored the reversible photostructural effects and metastable photorefraction in As₄Se₃ films by using the VASE, and the results were analyzed by a simple model consisting of the Cauchy dispersion formula. They found that the as-deposited film has a maximum refractive index compared with the annealed and irradiated films, and significant metastable reversible photorefraction is accompanied by photodarkening.

Park et al. (2008)^[32] measured the dielectric functions of (GeTe, Sb₂Te₃) pseudobinary thin films by using SE. The refractive indices of the annealed crystalline thin films were found to increase significantly with increasing Ge content compared with those of the as-grown films, whereas those of the other films only increase slightly with increasing Sb₂Te₃ content. Both the refractive index (n) and extinction coefficient (k) were found to increase substantially once the thin films were transformed from amorphous to crystalline phase.

Todorov et al. (2009)^[33] investigated the optical properties of thin As–S–Se films and found that in binary As_xS(Se)_100−x systems, As₄₀S₆₀ and As₄₀Se₆₀ have maximum refractive indices of 2.458 and 3.301, respectively. In the As–S–Se system, the refractive index decreases with As content decreasing, but increases with Se content increasing. While the films are exposed to light irradiation, their refractive indices were found to increase due to the photodarkening effect.

Lee and Ku (2010)^[17] prepared Ge₉₀Te₁₀ films by electron beam evaporation at different values of substrate temperature (T_s) and deposition rate (R) and characterized their optical properties by SE. They used the G oscillator function for analyzing the VASE in the mid-IR range of film, and found that T_s rather than R has a stronger effect on the crystallinity of the film. The extinction coefficient of the Ge₉₀Te₁₀ film was found to be close to zero in the 3 μm–12 μm region, which is similar to those in Refs. [34] and [35]. They also found that optimal deposition conditions are R within 0.9 nm/s–1.5 nm/s at T_s = 200°C, under which the film has low absorption and high refractive index.

Němec et al. (2011)^[19] noted that in all the cases, thickness nonuniformity, thickness of the thin film and the surface layer were also fitting parameters. The low values of MSE show that the CL model for analysing the VASE data is appropriate for describing the optical characteristics of Ge–Sb–Te thin films.

Kang et al. (2012)^[36] used the TL and Lorentz oscillator function for analyzing the VASE data of the crystalline and amorphous Ge-doped SbTe thin films, respectively. For crystalline thin films, they added the Drude model dielectric function to incorporate free carrier effects.

Yim et al. (2014)^[37] employed SE to characterize E_g, thickness and other optical constants of two-dimensional materials such as MoS₂, WTe₂ and MoSe₂. They built a four-layer physical structure model (MoS₂/SiO₂/interface layer/Si) to extract the data and successfully used a TL model to determine the optical properties of the MoS₂ thin film.

Thermally evaporated In_x(As₂Se₃)_1−x (x = 0, 0.01, 0.05) films were also characterized by VASE.^[38] The refractive index and E_g were found to decrease while the absorption coefficient increases with In content increasing. The real and imaginary part of the dielectric function, ε₁ and ε₂ were also calculated, and the results showed that ε₁ decreases while ε₂ increases with In content increasing.

In order to find whether there is good agreement between VASE and a spectrophotometer, Shaaban et al. (2015)^[39] measured the optical properties of ZnSe_1−xTe_x (0.0 ≤ x ≤ 1.0) thin films by these two different methods. With the addition of tellurium content in a range of 400 nm–1100 nm at room temperature, the refractive index of the polycrystalline ZnSe_1−xTe_x increases gradually while the optical band gap decreases from 2.59 eV to 2.16 eV. As a result, there is good agreement between spectrophotometry analyses and the results from VASE.

Guo et al. (2015)^[40] recently explored the relation between optical property and local structural change in tungsten (W)-doped Ge₂Sb₂Te₅ (GST) by VASE at high temperature. The TL and Drude dispersion models were used for evaluating the dielectric function, which changes from 210 K to 660 K. A single TL model was used to obtain optical properties in the UV-vis region of 0.6 eV–4.13 eV. The TL + Drude model was used in the IR region of 0.2 eV–0.6 eV. The ε₂ peaks from amorphous to crystalline phase for GST and GSTW films showed redshifts with the increase of W concentration for the amorphous phase in the UV-vis region of 0.6 eV–4.13 eV. On the contrary, they showed blueshifts for the crystalline phase. Accompanied by an increase in W concentration, the values of Tauc gap energy (E_g) for crystalline and amorphous films were both monotonically decreased. They analyzed the dielectric function and found that the band gap narrows by W doping during phase change. They observed up to four transition regions in the band gap evolving with temperature and derived the corresponding temperature coefficients.

Guo et al. (2016)^[41] further measured the dielectric function 〈ε〉 of W-doped Sb₂Te phase change thin films by using temperature regulated VASE type SE. Due to its high absorption, the dielectric function 〈ε〉 was analyzed via surface roughness and isotropic main layer model from the parameters (ψ, Δ). They used single TL and Lorentz dispersion models to analyze VASE data of amorphous and crystalline films, respectively, and extracted the dielectric functions of Sb₂Te and silicon-doped Sb₂Te films with a five-layered structure model (air/surface rough layer/SST/SiO₂/Si) (see Ref. [22]).

Velea et al. (2015)^[42] in-situ measured optical properties of GeTe and GaSb thin films during the transition from the amorphous to crystalline phase by a Woollam vertical-variable angle spectroscopic ellipsometer (V-VASE). The maximum of the optical dielectric function was found to be larger in the transition from amorphous to crystalline phase, which was attributed to a significant change in chemical bonding between the two phases. The refractive indices changed from 1.6 to 4.7 for the as-deposited GeTe films and from 0.7 to 7.0 for the annealed GeTe, and the refractive index varied between 1.5 and 4.8 in the as-deposited GeSb films and between 1.4 and 4.8 in the annealed on the whole wavelength domain, respectively.

Abdel-Wahab et al. (2016)^[43] investigated the annealing effect on the optical properties of the Ge₅Te₂₀Se₇₅ thin film in a spectral range from 245 nm to 1700 nm. They compared individual TL and CL dispersion models and linear combinations of the TL or CL model with multiple G models. It was demonstrated that while the individual TL and CL models were not appropriate, reasonable good results could be achieved by using both the CL + 3 G and TL + 3 G models for the optical characterization of these films. It was found that the maximum value of the refractive index (n) was shifted toward the longer wavelength by increasing the annealing temperature.

Table 3.

Table 3.

Table 3. Recent applications of the ellipsometer in chalcogenide thin films. . Component Model Spectral range Angle Physical structure model Dispersion relationship Ref. As4Se3 VASE, J A Woollam Co., Inc. 0.5 μm–2.3 μm 65°, 70°, 75° Surface roughness/Cauchy/substrate – [31] GeTe/Sb2Te3 VASE, J A Woollam Co., Inc. – 65°, 70°, 75° Surface roughness/isotropic main layer/SiO2 layer/Si substrate – [32] Ge90Te10 IR-VASE® J A Woollam Co. 3 μm–12 μm – – G model [17] MoS2 – – – MoS2 layer/interface layer/SiO2 layer/Si substrate TL model [37] Inx(As2Se3)1−x (x = 0, 0.01, 0.05) VASE, J A Woollam Co., Inc. 1.9 eV–4.5 eV 45°, 50°, 55° – – [38] ZnSexTe1−x J A Woollam, M-2000 0.4 μm–1.1 μm 65°, 70°, 75° Rough layer/“B-Spline”absorbing ZnSexTe1−x layer/glass substrate – [39] W doped Ge2Sb2Te5(GSTW) VASE, J A Woollam Co., Inc. 0.3 μm–6.2 μm 70° Air/surface rough layer/GSTW/SiO2/Si TL and Drude models [40] GeTe/GaSb V-VASE 0.275 μm–1.77 μm 70° – TL model [42] Ge5Te20Se75 J A Woollam, M-2000 0.245 μm–1.7 μm 55°, 65°, 75° ambient medium (air)/surface rough-ness layer/Ge5Te20Se75 layer/glass substrate CL + 3 G/TL + 3G [43]

Table 3. Recent applications of the ellipsometer in chalcogenide thin films. .

The table shows that the reliability of the ellipsometric results depends largely on the structural modeling and material dispersion relationship. Different fitting results can be obtained by using different dispersion relations for the same material. Even if the material dispersion relation has been established, it is possible to obtain different results if the different physical layer structures are used. In order to obtain accurate parameters from VASE, selecting a proper dispersion model is important. For example, TL and CL models, which are KK consistent, have been shown to be able to provide accuracy for analyzing amorphous semiconductor data. However, the CL model is useful for serving as a fitting model.

In this paper, we have reviewed the principle of ellipsometry and the data analysis model, as well as the applications of VASE in the characterization of chalcogenide bulk glasses and thin films. It is found that any single data analysis model cannot be perfectly used to fit the optical constants of the chalcogenide bulk glasses and thin films over a wide wavelength range. Instead, a combination of various models is demonstrated to be useful for characterizing the optical properties of the materials accurately. Moreover, since the applications of chalcogenide glasses are mostly in a wavelength range from 1 μm to 20 μm, the optical constants in the mid-and far-infrared region are essential to developing the applications. However, the optical data are limited in this wavelength range, which might be due to the limited light source available in this wavelength range. Instead, SE provides a flexible and reliable way to measure the optical constants in the mid-and far-infrared region, implying its great potential in characterizing the optical properties of chalcogenide glasses.