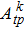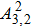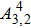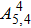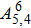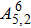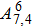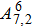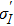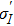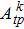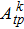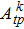Project supported by the National Natural Science Foundation of China (Grant Nos. 61405206, 51502292, and 51702322), the Knowledge Innovation Program of the Chinese Academy of Sciences (Grant Nos. CXJJ-16M251 and CXJJ-15M055), and the National Key Research and Development Program of China (Grant No. 2016YFB0402101)
Project supported by the National Natural Science Foundation of China (Grant Nos. 61405206, 51502292, and 51702322), the Knowledge Innovation Program of the Chinese Academy of Sciences (Grant Nos. CXJJ-16M251 and CXJJ-15M055), and the National Key Research and Development Program of China (Grant No. 2016YFB0402101)
† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 61405206, 51502292, and 51702322), the Knowledge Innovation Program of the Chinese Academy of Sciences (Grant Nos. CXJJ-16M251 and CXJJ-15M055), and the National Key Research and Development Program of China (Grant No. 2016YFB0402101)
The Yb:YAG is an excellent high-average power and ultra-short pulse laser crystal. Transition intensity parameters 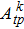
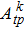
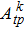
The Yb3+:YAG is an important high-power laser material used in the diode pumped solid state laser (DPSSL), which has high thermal conductivity, good mechanical property, high chemical and physical stability and excellent large crystal growth properties, and has received great attention. Rutherford et al. predicted that it can be used to obtain 100-kW edge-pumped DPSSL.[1] A continuous-wave average output power of 2.65 kW from a single composite Yb:YAG laser rod with (0.6 at.%) Yb:YAG of ϕ4 mm × 80 mm pumped with 9000 W from 940-nm InGaAs laser diodes has been reported.[2] Lucia laser in French could deliver a 100 Joules/10 ns/10 Hz pulse train from ceramic/crystal Yb:YAG,[3] and a 64-J at 10-ns output was demonstrated by diode-pumped cryogenically cooled Yb:YAG ceramic laser amplifier recently.[4] It has been also used to develop few-cycle, waveform-controlled light pulses with a repetition rate of 10 Hz and a peak power in the petawatt regime in petawatt field synthesizer in Germany.[5] A 7.07-kW Yb:YAG composite crystal zigzag slab amplifier at room temperature was developed and demonstrated with an optical-to-optical efficiency of about 29.5% and a slope efficiency of 39.5% by Li et al. in Institute of Applied Electronics, China Academy of Engineering Physics.[6]
Patel et al. reported the crystal growth, spectral, thermal and laser properties.[7] Due to the fact that f–f transitions of Yb3+ are very few in number, which is usually far less than the number of the crystal field parameters 
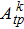
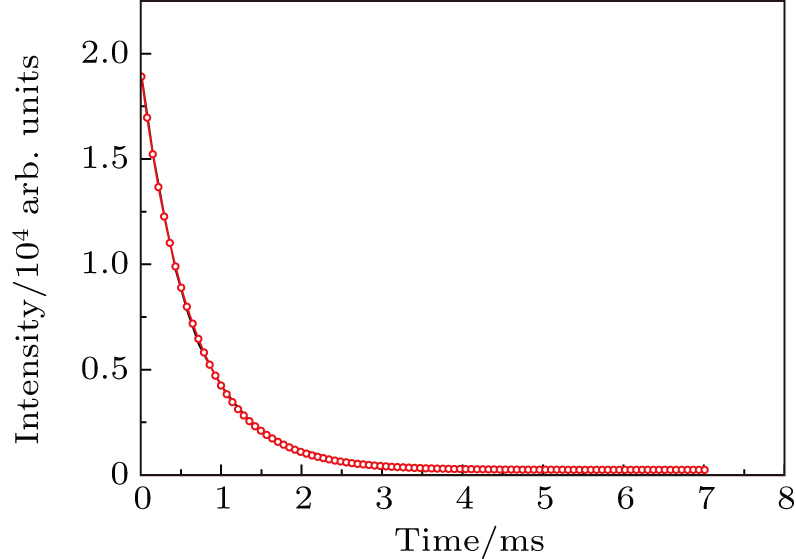
(10 at.%) Yb:YAG was grown by the Czockralski method in a furnace JGD60, made in the 26th Institute, China Electronics Technology Corporation (CETC) in China, and its photoluminescence spectra at 8 K and 300 K were measured under the light excitation of 914.8 nm with Fluorolog-3-Tau made in JOBIN YVON in France. The photoluminescence decay curve was measured at a monitor wavelength of 1028.2 nm and an excitation wavelength of 914.8 nm, which is a single exponential decay with decay constant 643 μs and shown as in Fig.
The Yb3+ dopants in YAG replace Y3+ ions and occupy the site symmetry D2, which results in nine non-vanished pure imaginary intensity parameters 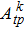
| Table 1. Initial and fitted parameters of |
The crystal field energy levels of Yb3+ in YAG have been evaluated in Ref. [11], which is denoted as |J, Γi〉(r), where Γi is point group irreducible representation, r represents the multiplicity of |J, Γi〉. |J, Γi〉(r) refers to the dominant component of the corresponding wavefunctions. For convenience, the energy levels of Yb:YAG are labeled as Ei (i = 1, 2, 3, 4, 5, 6 and 7) form low to high energy, which is 0, 564, 606, 787, 10329, 10629, and 10829 in unit cm−1 (wavenumber). The calculated photoluminescence emission intensity of Yb3+, including electric and magnetic dipole transitions, can be expressed as[9]
 |
In order to eliminate the arbitrariness resulting from measurement, the transition intensity and energy life time of |5/2, Γ1〉 (1) with E1 are fitted at the same time to the following equation:[9]
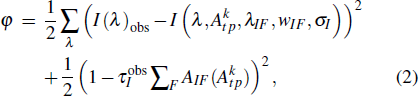 |

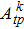
 |
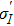
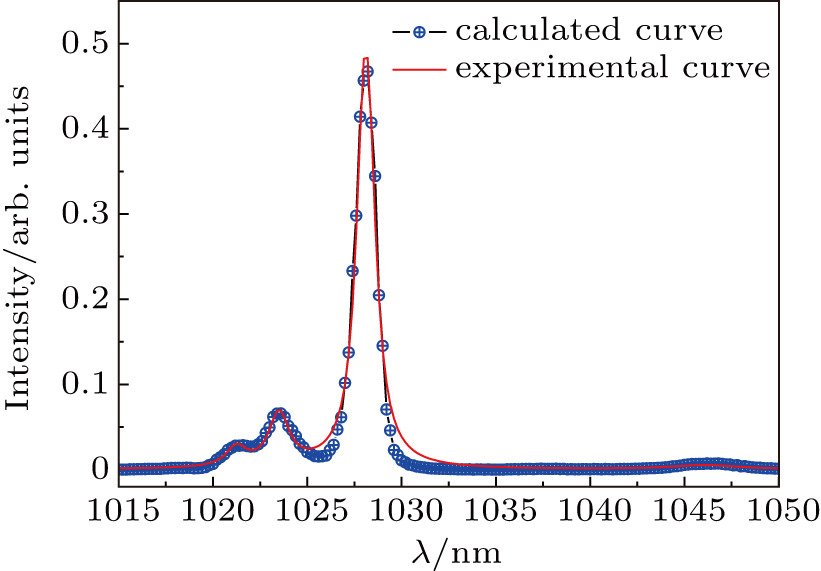
Three pure electron state transitions, which correspond to the emission peaks at 1023.5 nm, 1028 nm, and 1046.1 nm, and three vibronic coupling transitions peaking at 1021.4 nm and 1028.28 nm, which mean that Yb3+ absorbs a phonon of 22 cm−1 and releases a phonon of 3.0 cm−1, were used to fit the emission spectrum of Yb:YAG at 8-K temperature.
Fifteen variables, including nine transition intensity parameters 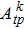
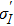
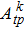
Due to the high dopant concentration, the fluorescence quenching is obvious. According to Ref. [12], the decay time of Yb3+:YAG is 950 μs, and its temperature dependence is not obvious. So the decay time of 950 μs is also used to fit the transition intensity parameters of Yb:YAG again. After 20 iterations, R reaches 12.1%, and the calculated decay time of E5 is 953 μs. Next, the obtained 
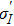

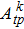

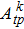
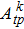
| Table 2. Values of transition probability A, line strength S, fluorescence branch ratio β of Yb3+:YAG at 8 K. . |
The transition probabilities and line strengths of Yb:YAG are listed in Table
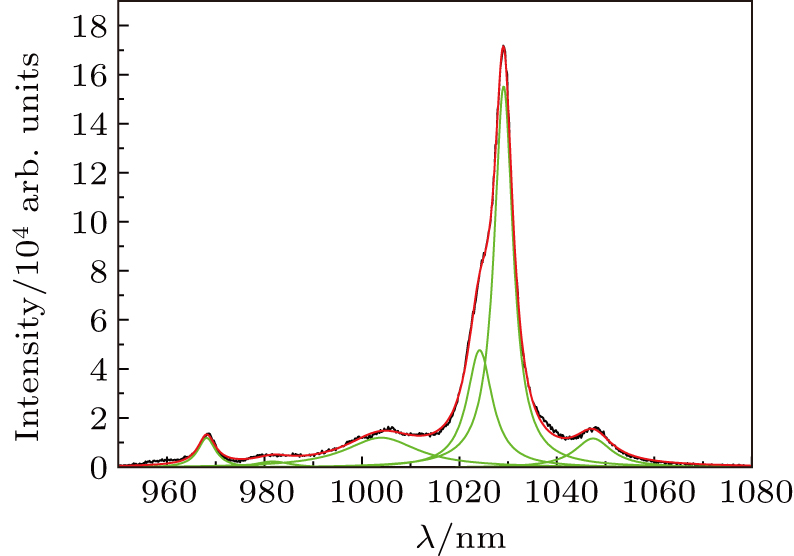
The emission spectrum of (10 at.%) Yb:YAG excited by the light of 914.8 nm is shown in Fig.
| Table 3. Fitted results of the room temperature emission spectra of (10 at.%) Yb:YAG with Lorentz profile. . |
The emission band with peak 981 nm should be from the vibronic band of E5 → E1 of Yb:YAG, and has the same initial state as the emission band with peak 968.1 nm. When the temperature increases, the lattice vibration intensifies, and the corresponding phonon energy should increase. So it is suggested that the emission bands of 1000.8 nm and 1006.5 nm are from the vibronic bands of E5 → E2, which means that the transition with one-phonon assisted transition at low temperature has turned into two-phonon assisted transitions with energies of 172 cm−1 and 228 cm−1, respectively.
Due to the strong re-absorption near 968 nm, the emission spectrum as shown in Fig. 
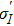
 | Fig. 4. (color online) Fitted and experimental emission spectra of (10 at.%) Yb:YAG at 300 K (λex = 914.8 nm). |
| Table 4. Parameters fitting the emission spectrum of (10 at.%) Yb:YAG at room temperature. . |
| Table 5. Values of transition probability A, line strength S, fluorescence branch ratio β of Yb3+:YAG at 300 K. . |
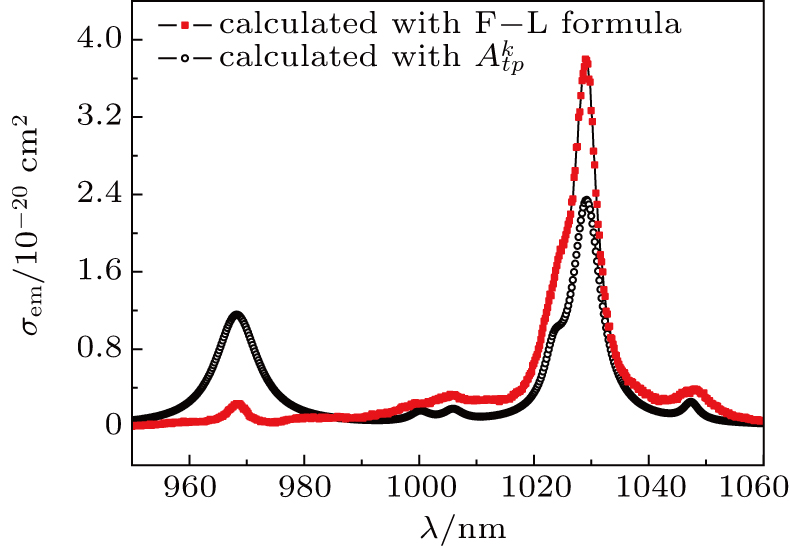
Emission cross section is a gain ability parameter of a laser medium and can be used to evaluate its laser performance directly. Because there exists an obvious concentration quenching in (10 at.%) Yb3+:YAG, so its emission cross section is calculated by 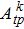
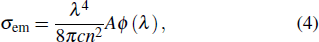 |
 |
As a comparison, the emission cross section of Yb3+:YAG is calculated by Fuchtbauer–Ladenburg (F–L) equation[7]
 |
The emission cross sections at 8 K calculated by Eqs. (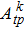
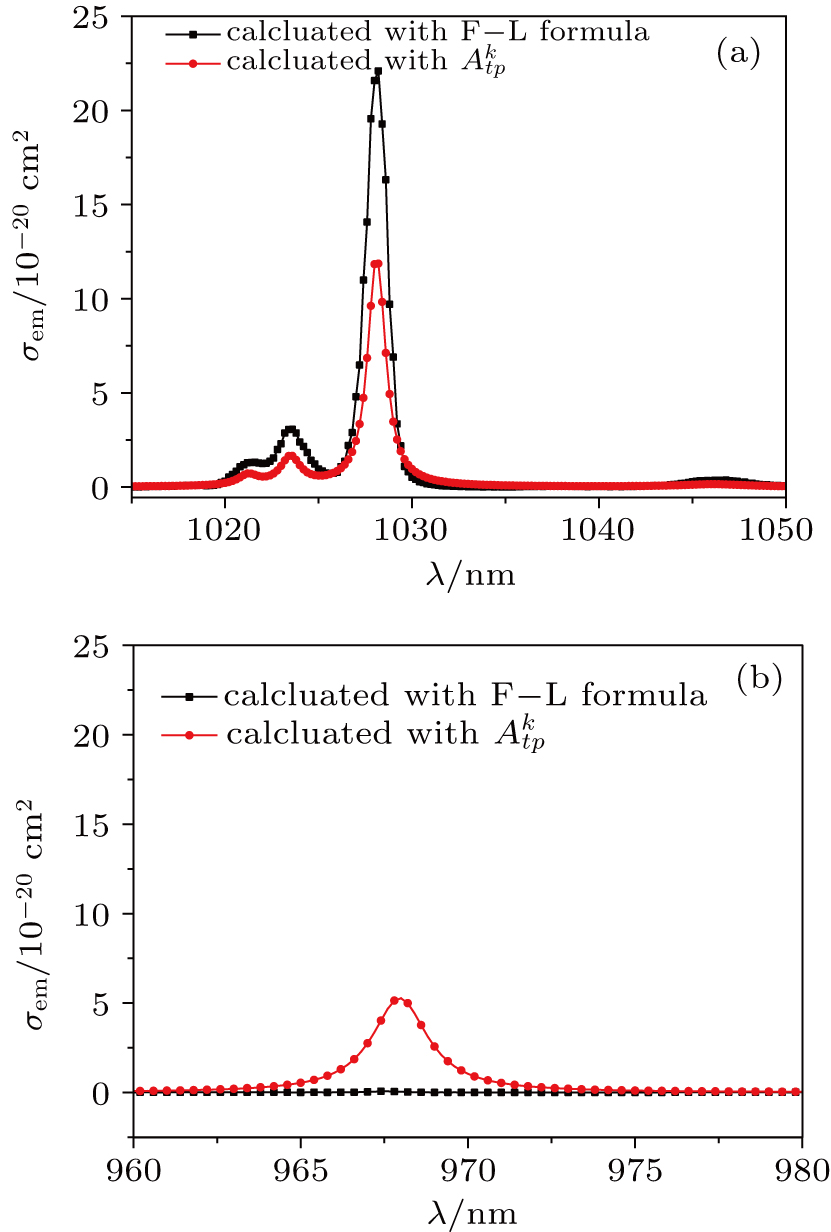 | Fig. 5. (color online) Emission cross sections of Yb:YAG, calculated by intensity parameters 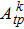 |
| Table 6. Values of emission cross section σem (in 10−20 cm2) of Yb3+:YAG, calculated with |
The emission cross sections at 300 K are also calculated by 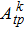
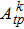
According to Judd–Ofelt triple parameter intensity formula, if the crystal field energy level splitting is omitted, the dipole transition line strength of 2F5/2 →2 F7/2 can be calculated by
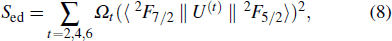 |
In summary, the emission spectrum of Yb3+:YAG at 8 K consists of four pure electron state transitions and two-phonon assisted transitions, one vibronic transition releases a phonon, and the other vibronic transition absorbs a phonon in the frame of the single frequency approximation. In the emission spectrum at 300 K, there exist one vibronic transition releasing a phonon, and two vibronic transitions absorbing a phonon. The optical transition procedure absorbing phonon can reduce the thermal load of Yb3+:YAG and improve its thermal management. Emission cross sections determined by F–L formula are remarkably different from those calculated by 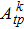
Transition intensity parameters 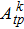
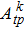
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] |