Project supported by the National Basic Research Program of China (Grant No. 2014CB643702), the National Natural Science Foundation of China (Grant No. 51590880), the Knowledge Innovation Project of the Chinese Academy of Sciences (Grant No. KJZD-EW-M05), and the National Key Research and Development Program of China (Grant No. 2016YFB0700903).
Project supported by the National Basic Research Program of China (Grant No. 2014CB643702), the National Natural Science Foundation of China (Grant No. 51590880), the Knowledge Innovation Project of the Chinese Academy of Sciences (Grant No. KJZD-EW-M05), and the National Key Research and Development Program of China (Grant No. 2016YFB0700903).
† Corresponding author. E-mail:
Project supported by the National Basic Research Program of China (Grant No. 2014CB643702), the National Natural Science Foundation of China (Grant No. 51590880), the Knowledge Innovation Project of the Chinese Academy of Sciences (Grant No. KJZD-EW-M05), and the National Key Research and Development Program of China (Grant No. 2016YFB0700903).
Data-mining techniques using machine learning are powerful and efficient for materials design, possessing great potential for discovering new materials with good characteristics. Here, this technique has been used on composition design for La(Fe,Si/Al)13-based materials, which are regarded as one of the most promising magnetic refrigerants in practice. Three prediction models are built by using a machine learning algorithm called gradient boosting regression tree (GBRT) to essentially find the correlation between the Curie temperature (TC), maximum value of magnetic entropy change ((ΔSM)max), and chemical composition, all of which yield high accuracy in the prediction of TC and (ΔSM)max. The performance metric coefficient scores of determination (R2) for the three models are 0.96, 0.87, and 0.91. These results suggest that all of the models are well-developed predictive models on the challenging issue of generalization ability for untrained data, which can not only provide us with suggestions for real experiments but also help us gain physical insights to find proper composition for further magnetic refrigeration applications.
The magnetocaloric effect (MCE), reversible entropy or temperature variation upon the change of external magnetic fields, is an inherent quality of magnetic materials. Magnetic refrigeration (MR) based on MCE is becoming a great topic of current interest on account of the potential improvement in environmental friendliness and high efficiency compared to the conventional vapor compression methodology. MCE materials are usually characterized in terms of the maximum value of magnetic entropy change ((ΔSM)max) in an isothermal process, and the Curie temperature (TC) around which the material works. In the last two decades, significant progress has been made in exploring large MCE materials for applications at low and room temperatures. Typical low temperature MCE materials mainly include the rare earth-based intermetallic compounds, such as RCo2,[1,2] RNi,[3] etc. However, more attention has been paid to room temperature MCE materials because of their potential applications in refrigerators and air conditioners. These MCE materials mainly include Gd5Si2Ge2,[4,5] MnAs1 − x Sbx,[6] MnFeP1 − x Asx,[7] Heusler alloys,[8,9] etc.
Among these MCE materials, La(Fe,Si/Al)13-based compounds are commonly approved as one of the most promising magnetic refrigerants. The binary LaFe13 phase does not exist as a result of its positive formation enthalpy.[10] Therefore, a third element, either Si or Al, had to be introduced to stabilize a cubic NaZn13-type structure. For La(Fe,Si/Al)13-based compounds, there are many studies focusing on improving its MCE performance by, for example, changing the Fe and Si/Al content,[10,11] doped transitional metal (Co and Mn),[12,13] rare earth (Ce, Pr, Nd),[14–16] interstitials (H, C, B),[17–19] etc. When the chemical composition of La(Fe,Si/Al)13-based compounds is changed, (ΔSM)max and TC may also change. Predicting these physical features is not easy when the composition is complex. However, data-mining techniques using machine learning can be applied to build models for the prediction of the relationship between physical features with composition-related parameters that can be obtained prior to experiment.
Machine learning is a field of computer science that provides computer systems with the ability to “learn” (i.e., progressively improve performance on a specific task) from data without being explicitly programmed. Machine learning is widely used in many fields after decades of development. It can build a predictive model between features and target property by using statistical rules from massive experimental data. It is a powerful method to analyze large volume and multidimensional data that are perfectly matched for materials design. Materials design that involves machine learning has been used successfully in various research fields.[20–24] For example, Anton et al.[22] built a machine learning model to make fast and reliable predictions of the occurrence of Heusler versus non-Heusler compounds for an arbitrary combination of elements with no structural input on over 4 × 105 candidates. Xue et al.[23] built a model between composition and thermal hysteresis (ΔT) in Ti50Ni50−x−y−z CuxFeyPdz shape memory alloys and ultimately discovered 14 new compounds possessing smaller ΔT than the original dataset from a potential space of ∼ 8 × 105 compositions. Similar methods were also used in the MCE field. Taoreed et al.[24] built a model to predict the Curie temperature (TC) of manganite-based materials in different dopants that found a proper manganite quickly.
To date, data-mining techniques using machine learning have not been reported in the materials design of La(Fe,Si/Al)13-based compounds. In this paper, we successfully developed prediction models using a machine learning algorithm called gradient boosting regression tree (GBRT)[25] to predict the maximum value of magnetic entropy change ((ΔSM)max) and the Curie temperature (TC) of La(Fe,Si/Al)13-based materials based on chemical composition, which have the potential to boost the speed of composition design research fundamentally and provide implications for solving the challenging and elusive issue of finding a proper composition for further application.
The dataset of La(Fe,Si/Al)13-based materials was collected from the published literatures and contained 144 pieces of data.[26] Noting that the divergences of phase, Curie temperature, and (ΔSM)max for materials may reduce the accuracy of models’ prediction, all of the data we collected here are guaranteed to be NaZn13-type structure, and the values of Curie temperatures and (ΔSM)max are reliable for model learning. The data feature we used here is chemical composition, and the target properties we predicted are Curie temperature TC and (ΔSM)max under a magnetic field change of 0 T–2 T and 0 T–5 T, respectively. Because some data from the dataset may not contain all three of the target properties, the dataset we used to build the prediction model for each target property is not the same. For each target, we used 141 data points for TC, 108 for (ΔSM)max at 0 T–2 T, and 93 for (ΔSM)max at 0 T–5 T.
The task we faced in supervised learning of traditional machine learning field is a regression problem. The algorithms that can handle this task mainly contain linear regression, decision tree regression, support vector regression, and some ensemble methods. The algorithm we used here is GBRT, which belongs to the ensemble methods. The GBRT algorithm produces a prediction model in the form of an ensemble of weak prediction models, which is an ensemble of regression tree models. The algorithm trains weak regression tree models once to make a weak prediction each time. Although the prediction errors are large at first, the algorithm will iterate training new weak regression trees to make the prediction better. Each new tree helps to correct errors made by the previously trained trees. Boosting is based on the idea of whether a weak model can be modified to become better. There are two important parameters in the GBRT algorithm: one is the number of estimators, which means the number of weak regression tree models; the other is the learning rate, which means the speed of improvement during iterating training weak regression trees. The GBRT algorithm is considered to be one of the best methods in machine learning. It can fit data where the relationship between features and target properties is complex well and perform robustly when facing outliers.
From the dataset, we used the chemical composition as a data feature and Curie temperature (TC) and (ΔSM)max as target properties. Our models will learn from the data to predict target properties via some features. The overall setup for prediction models is shown in Fig.
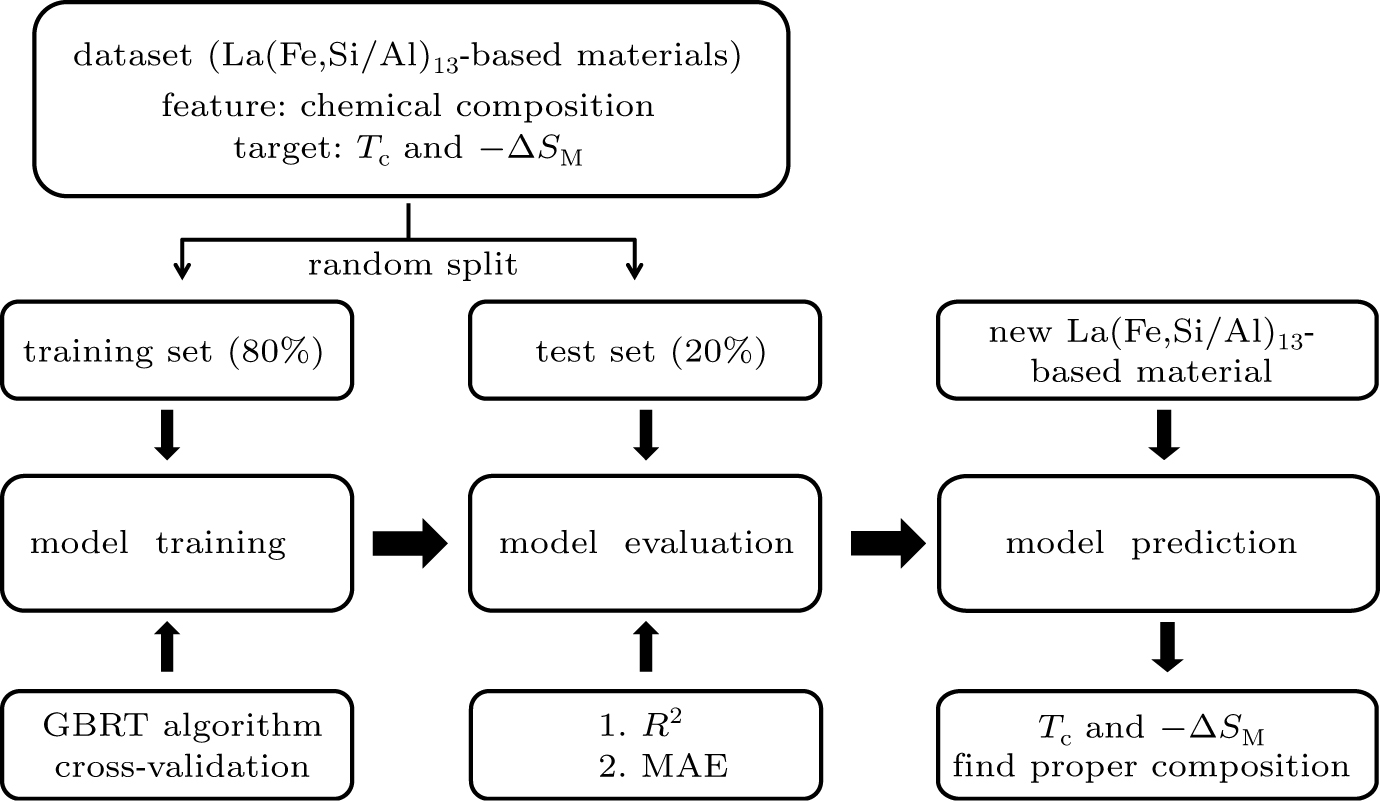 | Fig. 1. Overall setup processes for prediction models by using machine learning approach on La(Fe,Si/Al)13-based materials. |
(i) Split the dataset into two parts: training set and test set. The training set is used to train the model, and the test set is used to evaluate the performance of the trained model. In general, the training set is 80% of the entire dataset, and the test set is 20%. To optimize performance, the dataset must be split randomly.
(ii) Build the GBRT model. Then, search for the best parameters of the model by the grid-search method.[27] The performance metric is R2 for the model prediction of training set after using k-fold cross-validation. R2 represents the variance explained by the model (the higher, the better), and its maximal value is equal to 1.
(iii) Evaluate the model’s predictive performances on the test set, as soon as model training finished. The metrics are R2 and MAE (mean absolute error: the lower, the better).
Finally, the model can be used to estimate target properties for new materials via inputs of chemical composition, which can serve as a quick guide to composition design and help find proper materials.
In this paper, all of the models’ setup and analysis are implemented in Python 3.6 with the scikit-learn open-source package.
We used 108 data points to train the TC prediction model. The data distribution is counted. As shown in Fig.
After the best model is trained, it needs to be evaluated to determine whether it is feasible. A general way is to use the test set for the untrained data. The metrics we used to evaluate are R2 and MAE. The results are depicted in Fig.
The number of data points used to train (ΔSM)max prediction models for 0 T–2 T and 0 T–5 T is 108 and 93, respectively. The data distributions are shown in Figs.
After training the best models, we use the test set to evaluate the models. The metrics and process are the same as for the TC prediction model. The two models’ results are shown in Fig.
 | Fig. 5. (color online) Predicted scatter plots on (ΔSM)max at 0 T–2 T and 0 T–5 T datasets. (a) and (c) Training set, (b) and (d) test set. |
All of the models we built above have good predictive performance. The model with (ΔSM)max at 0 T–2 T performs similarly to that with (ΔSM)max at 0 T–5 T. Compared to the (ΔSM)max prediction models, the TC prediction model has better performance. Because the datasets of the three models possess similar size, the phenomenon may result from the magnetic properties that the models predict. The Curie temperature, TC, is an intrinsic magnetic property for materials that is hardly affected by the measurement methods. By contrast, (ΔSM)max is a calculated value from experimental results, and is sensitive to the detailed measurement methods and experiments. Considering the complexity of obtaining (ΔSM)max, the datasets for (ΔSM)max may be of larger errors, which may give rise to more uncertainty to predicate (ΔSM)max than TC.
In summary, we successfully developed three prediction models using a machine learning algorithm called GBRT to predict two important magnetic properties of MCE materials: (ΔSM)max and TC, respectively, for La(Fe,Si/Al)13-based materials based on the chemical composition. Based on this model, the properties of untrained data can be well predicted. Our findings suggest that machine learning is very powerful and efficient tools which can be used to accelerate composition design and find proper composition for further applications in practice.
In addition, the selection and construction of features are the most important factors affecting the performance of the models. In further research, additional physical properties, such as lattice constant and saturation magnetization, should be included in the features as they can greatly affect the target properties. Constructing more physical features for models may significantly improve the performance.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] |




