Project supported by the Key Basic Research Program of China (Grant Nos. 2015CB921401 and 2016YFA0300503), the National Natural Science Foundation of China (Grant Nos. 11422429 and 11421404), China Postdoctoral Science Foundation (Grant No. 2016T90332), the Program for Professor of Special Appointment (Eastern Scholar) at Shanghai Institutions of Higher Learning, and STCSM of China (Grant No. 15XD1500200), and the Strategic Priority Research Program (B) of the Chinese Academy of Sciences (Grant No. XDB04040200).
Project supported by the Key Basic Research Program of China (Grant Nos. 2015CB921401 and 2016YFA0300503), the National Natural Science Foundation of China (Grant Nos. 11422429 and 11421404), China Postdoctoral Science Foundation (Grant No. 2016T90332), the Program for Professor of Special Appointment (Eastern Scholar) at Shanghai Institutions of Higher Learning, and STCSM of China (Grant No. 15XD1500200), and the Strategic Priority Research Program (B) of the Chinese Academy of Sciences (Grant No. XDB04040200).
† Corresponding author. E-mail:
Project supported by the Key Basic Research Program of China (Grant Nos. 2015CB921401 and 2016YFA0300503), the National Natural Science Foundation of China (Grant Nos. 11422429 and 11421404), China Postdoctoral Science Foundation (Grant No. 2016T90332), the Program for Professor of Special Appointment (Eastern Scholar) at Shanghai Institutions of Higher Learning, and STCSM of China (Grant No. 15XD1500200), and the Strategic Priority Research Program (B) of the Chinese Academy of Sciences (Grant No. XDB04040200).
We performed ultra-low temperature thermal conductivity measurements on the single crystal of a new gold-based quasi-two-dimensional superconductor AuTe2Se4/3, which has a superconducting transition temperature Tc = 2.70 K. A negligible residual linear term κ0/T in zero magnetic field is observed, which suggests fully gapped superconducting state. Furthermore, the field dependence of κ0/T is similar to that of the multi-band s-wave superconductor BaFe1.9Ni0.1As2 at low field. These results reveal multiple nodeless superconducting gaps in this interesting quasi-two-dimensional superconductor with Berezinsky–Kosterlitz–Thouless topological transition.
Two-dimensional (2D) superconductivity has been extensively studied in recent years to explore exotic quantum phenomena, such as high-temperature superconductivity and various quantum phase transitions.[1–3] There are several ways to realize the 2D superconductivity as described below.
(i) It can be realized in ultra-thin films grown by molecular beam epitaxy method, e.g., in monolayer FeSe/SrTiO3 (Tc = 65 K),[1] ultra-thin Ga films (
(ii) The 2D superconductivity can be found in some particular interfaces or surfaces, e.g., the LaAlO3/SrTiO3 interface (Tc = 0.2 K),[6] the interface of an insulator and a metal La2CuO4/La1.55Sr0.45CuO4 (Tc exceeds 50 K),[7] and the surface of MoS2 thin flake by ionic liquid gating (the maximum Tc = 10.8 K).[8,9]
(iii) By vertically putting two graphene sheets together with certain twisted angles, both a Mott-like insulating state and a superconducting state (Tc ≈ 1.7 K) arise from the electrons localized in these 2D superlattices.[10,11]
(iv) An relatively easier way is to mechanically exfoliate thin flakes directly from bulk van der Waals (vdW) quasi-2D superconductors. Bi2Sr2CaCu2O8+x (Bi-2212) and NbSe2 have been successfully cleaved to atomic thin sheets with different thicknesses, in which superconductivity has been observed (Tc = 82 K for half-unit-cell Bi-2212 and Tc = 3.1 K for monolayer NbSe2, respectively).[12–15] In this context, it is important to find more attractive vdW quasi-2D superconductors.
Very recently, a new gold-based quasi-2D superconductor AuTe2Se4/3 has been discovered.[16] Despite that metastable Au1−xTex (0.6 < x < 0.85) compounds are superconductors with Tc between 1.5 K and 3.0 K,[17,18] calaverite AuTe2 is a non-superconducting compound.[19] By introducing Se atoms into AuTe2, electrons from Te have been attracted by the Se anions, and superconductivity with 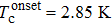
To understand the superconducting pairing mechanism of a new superconductor, it is crucial to know the superconducting gap structure first. In this work, we measure the ultra-low-temperature thermal conductivity of AuTe2Se4/3 single crystal down to 100 mK, to determine its superconducting gap structure. A negligible residual linear term κ0/T in zero field and a slow field dependence of κ0/T at low field are revealed, which suggest multiple nodeless superconducting gaps in this interesting vdW quasi-2D superconductor. This agrees with our previous band structure calculations in Ref. [16].
Single crystals of AuTe2Se4/3 were grown by the self-flux method.[16] The obtained single crystals have ribbon shape with shining mirror-like surfaces, as shown in the inset of Fig.
Figure
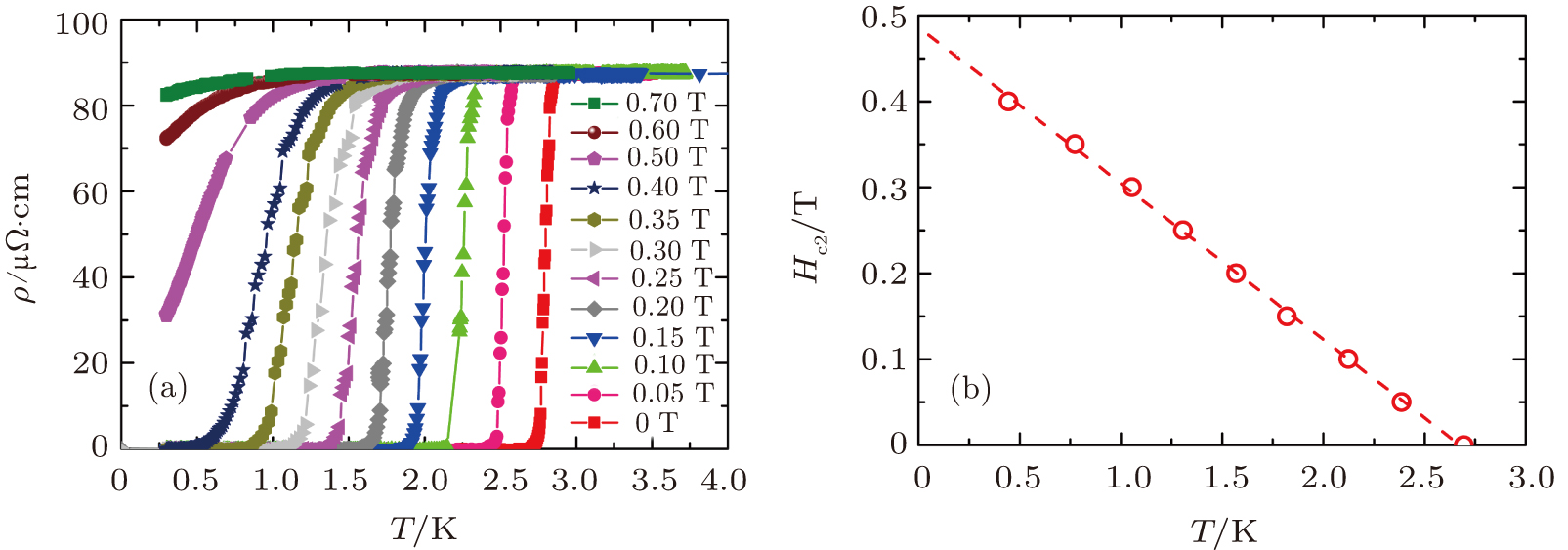
In order to estimate the upper critical field Hc2(0), the low-temperature resistivity of the AuTe2Se4/3 single crystal was measured in magnetic fields up to 0.7 T, as shown in Fig.
Ultra-low temperature thermal conductivity measurement is an established bulk technique to probe the superconducting gap structure.[24] The temperature dependence of thermal conductivity for the AuTe2Se4/3 single crystal in zero and magnetic fields is plotted in Fig.
In zero field, the fitting gives κ0/T = −9.9 ± 11 μW · K−2 · cm−1 and α = 2.41, as seen in Fig.
In Fig.
The field dependence of κ0/T can provide further information on the superconducting gap structure.[24] In Fig. 
 | Fig. 4. (color online) Normalized residual linear term κ0/T of AuTe2Se4/3 as a function of H/Hc2. For comparison, similar data are shown for the clean s-wave superconductor Nb,[30] the dirty s-wave superconducting alloy InBi,[31] the multiband s-wave superconductor NbSe2,[27] and iron-based superconductor BaFe1.9Ni0.1As2,[32] and an overdoped d-wave cuprate superconductor Tl-2201.[28] |
From Fig.
So far, among all multi-band s-wave superconductors, only the iron-based superconductors are unconventional with the possible s±-wave pairing.[34] Therefore, the multiple s-wave gap we observe in AuTe2Se4/3 indicates conventional superconductivity in it. This is reasonable, since unconventional superconductivity usually involves magnetism,[35] while AuTe2Se4/3 is nonmagnetic. As a new vdW quasi-2D superconductor, it will be interesting to fabricate AuTe2Se4/3 thin flakes to investigate whether its superconductivity can be enhanced by gating techniques, like in other quasi-2D compounds.[8,36–41]
In summary, the superconducting gap structure of the new gold-based quasi-2D superconductor AuTe2Se4/3 has been studied by the ultra-low temperature thermal conductivity measurements. A negligible κ0/T in zero field and the field dependence of κ0/T suggest multiple nodeless superconducting gaps. This is consistent with the band structure calculations which shows four Fermi surfaces in AuTe2Se4/3. To confirm those multiple gaps, further experiments like angle-resolved photoemission spectroscopy (ARPES) and scanning tunneling microscope (STM) are needed.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] |