Perovskites have a large family of compounds for the formula of ABX₃ (A = rare-earth, alkali or alkaline earth metal, B = transition metal).^[1–3] In the last few years, organic–inorganic hybrid perovskites ABX₃ (A = organic methylamine or formamidinium cation; B = Pb²⁺ or Sn²⁺; X = I⁻, Br⁻ or Cl⁻) formula as solar optical absorber materials were firstly reported by Miyasaka et al.^[4,5] Methylammmonium lead iodide perovskite (CH₃NH₃PbI₃), each Pb atom coordinates with six I atoms to form the PbI₆ group.^[6] Up to date, the three-dimensional (3D) perovskites structures consist of PbI₆ octahedra play an important role as the superior optical absorbing materials.^[7] With the increasing of temperature, the structure of CH₃NH₃PbI₃ has a transition from Pnma phases (orthorhombic, below 160 K) to I4/mcm (tetragonal) and Pm3-m (cubic) phases at 330 K and higher temperature, respectively. The main difference among three phases is the ordering of the noncentrosymmetric [CH₃NH₃]⁺ cation.^[8–13] The efficient solar cell absorbs a wide range spectra from 320 nm to 1000 nm, which are from the visible to near-infrared wavelengths range.^[14] The hybrid organic–inorganic perovskites have the power conversion efficiency (PCE) from 3.8% in 2009 to 22.1% in 2016, which are considered as promising materials in the optical field.^[15–24] The rapid development progress of CH₃NH₃PbI₃ has never been found in other solar cells in history. Organic–inorganic perovskites based on the metal hybrids solar cells have attracted wide photovoltaic research due to its flexibility, easy manufacture, low-cost and high optical absorption efficiency to scientific and industrial applications.^[25–36]

For the novel organic–inorganic perovskite materials, many efforts have been devoted to the replacement of A⁺, B²⁺, and X⁻ by other ions to exploring their outstanding performance.^[2,27] The hybrid organic–inorganic perovskites show excellent optical properties in recent experimental measurements and theoretical calculations.^[9] The most common strategic choice to the candidates is the Goldschmidt concept, which were proposed by Cheetham and co-workers.^[27,37] The ionic tolerance factor (τ) is to assess ionic radius size mismatches the following formed (Eq. (1)),

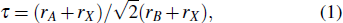In the paper, we presented a systematic computational investigation to study the effect arising from chlorine/bromine doping on the structural, electronic and optical properties of the CH₃NH₃PbI₃ perovskite based on density functional theory (DFT) calculations. The results indicate that the mixed perovskites have the larger band gap with the Cl⁻/Br⁻ amount increases and has lower optical absorption efficiency compare with the archetypal halide perovskites.

The following ab initio structural optimization and electronic properties on CH₃NH₃Pb(I_1−yX_y)₃ (X = Cl, Br; y = 0, 0.33, 0.67) perovskite structures were calculated by density functional theory (DFT) method with a plane-wave basis set, as implemented in Vienna Ab initio Simulation Package (VASP) code.^[45,46] The generalized gradient approximation (GGA) parametrized by Perdew–Burke–Ernzerhof (PBE)^[47] were adopted for the electron exchange–correlation energy functional. The electron–ion interactions were described by projected-augmented-wave (PAW)^[48] pseudopotentials with 1s¹, 2s²2p², 2s²2p³, 6s²6p², 3s²3p⁵, 4s²4p⁵, and 5s²5p⁵ and as valance electrons for H, C, N, Pb, Cl, Br, and I, respectively. All structures have been fully optimized by minimizing atomic forces and stress tensor components via the conjugate gradient algorithm. The Brillouin-zone (BZ) integration^[49] has been performed on a Monkhorst–Pack 4 × 2 × 4 k-mesh grid and the plane-wave cutoff is set to 400 eV in all configurations. Calculations were performed with and without spin–orbit coupling. The total electronic energy tolerance is set to 0.1 e⁻⁴ and the force converge for the structural relaxation is 0.001 eV/Å. The crystal structures were explained by using the VESTA program.^[50]

CH₃NH₃PbI₃ has the orthorhombic structure in the Pnma space group as shown in Fig. 1(a). The fully optimized lattice parameters are a = 8.437, b = 12.813, and c = 9.173Å, which were in good agreement with experimental values of 8.8362, 12.5804, and 8.5551Å,^[51,52] respectively, indicating the validity of our methodology and pseudopotential in application to the materials. The strong spin–orbit coupling (SOC) effects on reducing the conduction band structures of compounds consisting of heavy elements was studied by Even et al.^[53] Owing to the large SOC constant of lead atoms, effects of SOC on the band structure of CH₃NH₃PbI₃ is huge and cannot be disregarded.^[53,54] In Fig. S1 show significant changes of the electronic band structure when accounting for SOC. By comparison we can see that the conduction band is changed by the inclusion of the SOC and the bottom of the conduction band decreases obviously, while the valance band is nearly unaffected. As consequences, the band gap energy is reduced from 1.711 eV to 0.793 eV, which is in line with the results reported by Even et al.^[53] The valance band maximum (VBM) and the conduction band minimum (CBM) of CH₃NH₃PbI₃ are located at the G-point, the results of the direct semiconductor material are in line with the previous reported.^[42]

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. (a) The crystal structure of orthorhombic CH3NH3PbI3 with PbI6 octahedral. (b) The CH3NH3PbI3 unit cell used for modeling. Panels (c)–(d) display the unique arrangements for CH3NH3Pb(I1−yXy)3 when y = 0.33 and y = 0.67. Structures visualized with VESTA.

To address the effects of site different substitution concentrations, we consider two kinds of doping fractions of Cl⁻/Br⁻ (y = 0.33 and 0.67) within I sublattice (Figs. 1(c)–1(d). The optimized structure parameters, selected inter-atomic distances of CH₃NH₃PbI₃, and mixed halide structures are listed in Table S1 in Appendix A. Because of bigger ionic radius of I⁻ than Cl⁻/Br⁻, the partial doping of Cl⁻/Br⁻ with I⁻ lead to the reduction of lattice constants than pure CH₃NH₃PbI₃. The Cl atom has smaller radius compared with Br atom, which leads to a larger change of Pb–Cl distances.

Table S1.

Table S1.

Table S1. Calculated lattice parameters and selected inter-atomic distance (Å) for CH3NH3Pb(I1−yXy)3 (X = Cl, Br; y = 0, 0.33, 0.67) structures. . Orthorhombic halide structures Lattice parameters/Å Bond and distance/Å CH3NH3PbI3 a = 8.4384 Pb–I(1) × 2 3.315 b = 12.8117 Pb–I(2) × 2 3.215 c = 9.1733 Pb–I(3) × 2 3.185 Orthorhombic halide structures CH3NH3Pb(I0.67X0.33)3 Lattice parameters/Å Bond and distance/Å X = Br a = 8.4413 Pb–Br(1) × 2 3.029 b = 11.986 Pb–I (1) × 2 3.205 c = 9.237 Pb–I (2) × 2 3.219 X = Cl a = 8.4279 Pb–Cl (1) × 2 2.893 b = 11.382 Pb–I (1) × 2 3.208 c = 9.318 Pb–I (2) × 2 3.227 Lattice parameters/Å Bond and distance/Å X = Br a = 8.234 Pb–I (1) × 2 3.178 b = 12.550 Pb–Br(1) × 2 3.041 c = 8.718 Pb–Br(2) × 2 3.041 X = Cl a = 7.863 Pb- I(1) × 2 3.177 b = 12.494 Pb–Cl(1) × 2 2.932 c = 8.463 Pb–Cl(2) × 2 2.934

Table S1. Calculated lattice parameters and selected inter-atomic distance (Å) for CH3NH3Pb(I1−yXy)3 (X = Cl, Br; y = 0, 0.33, 0.67) structures. .

The perovskites with mixed halogen anions have different electronic and optical properties than Pb perovskites with pure halogen anions. To further investigate electronic properties of doping and pure CH₃NH₃PbI₃, the band structure, total density of states (DOS), and partial density of states (PDOS) for the doping systems of CH₃NH₃Pb(I_1−yX_y)₃ (X = Cl, Br; y = 0, 0.33, 0.67) are calculated. The calculated electronic band structures with and without spin–orbital coupling of the doping phases are shown in Fig. 2 and Figs. S1–S2 in Appendix A. Overall, all the considered configurations have quite similar direct band gaps and both the CBM and VBM were located at the G-point of the Brillouin zone. The bottom of the conduction band is changed by the inclusion of the SOC. As mentioned above, the Pb–Cl distances have changed more than the Pb–Br distance, which leads to Cl-doped perovskites that has a larger band gap than Br-doped perovskites. The band gap increases when iodine is replaced with chlorine/bromine atom, which implies that the absorption coefficients of the Cl/Br doped structure are lower. The result is inconsistent with previous reports that the Br-based structure shows similar trends in increasing of the band gap value with Cl-doped content increases.^[29]

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Electronic band structures of CH3NH3Pb(I1−yBry)3 with spin–orbital coupling for (a) y = 0.33, (b) y = 0.67 and CH3NH3Pb(I1−yCly)3 for (c) y = 0.33, (d) y = 0.67. The dashed line indicates the calculated Fermi levels.

From the PDOS of CH₃NH₃PbI₃ (Fig. S3), we can see that the VBM is mainly from the mixed contribution from 5p-orbitals of I, 6s-orbitals of Pb, and the CBM is mainly from 6p-orbitals of Pb. From the PDOS of Br-doped systems, as shown in Fig. 3 and Fig. S4, we can see that the addition of Br introduces the 4p-orbitals in the VBM. For y = 0.33, the VBM is still mainly 5p-orbitals of I (Fig. 3), mixed contribution from 5p-orbitals of I and 4p-orbitals of Br for y = 0.67 (Fig. S4). The p-orbitals of Pb constitute that the CBM remains unchanged. From the PDOS of Cl-doped systems, we can see that Cl-doped and Br-doped systems show the same phenomenon: for y = 0.33, the VBM is still mainly 5p-orbitals of I (Fig. S5), mixed contribution from 5p-orbitals of I and 3p-orbitals of Cl for y = 0.67 (Fig. S6). The 6p-orbitals of Pb constitute that the CBM remains unchanged. The [CH₃NH₃]⁺ consists of organic CH₃ and NH₃ two units, and the calculated PDOS are shown in Fig. 4 and Fig. S7. It is clearly shown that the sharp peaks belong to the strong orbital hybridization between the H 1s and C (N) 2p states, indicating the formation of the C–H and N–H covalent bonds. In conclusion, [CH₃NH₃]⁺ do not take part in the formation of the band and its major contribution is that it donates one electron to maintain the charge neutrality in materials, which is inconsistent with previously reported.^[31] Notable here is that the optical absorption coefficient is related to the electronic structure, which will be discussed in the following.

Fig. 3.

	Figure Option ViewDownloadNew Window
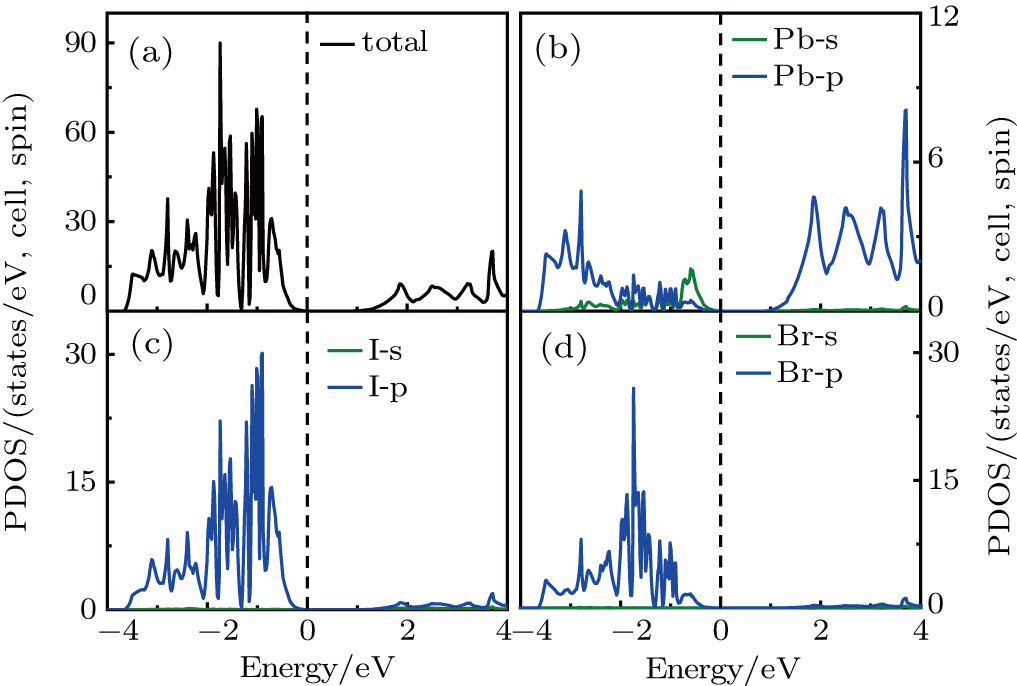	Fig. 3. Calculated spin-dependent total and partial density of states (PDOS) of CH3NH3Pb(I1−yBry)3 for y = 0.33. The dashed line indicates the calculated Fermi energy.

Fig. 4.

	Figure Option ViewDownloadNew Window
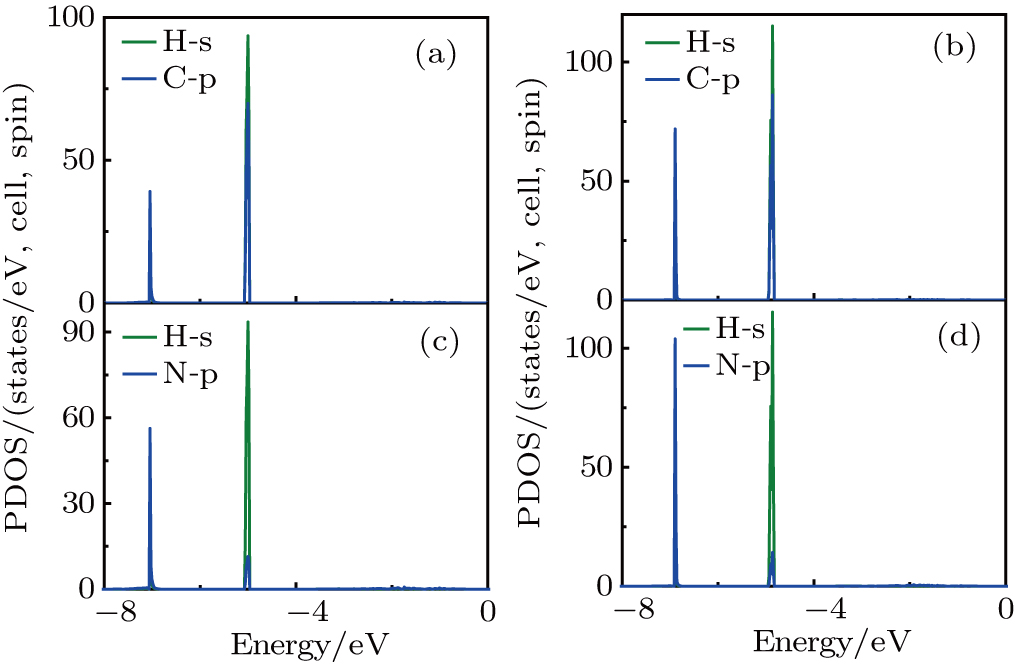	Fig. 4. Calculated spin-dependent partial density of states (PDOS) of CH3NH3Pb(I1−yBry)3 for y = 0.33 (a) and y = 0.67 (b).

The optical properties are important for organic–inorganic compounds, which can discover the potential applications in optoelectronic devices.^[55] The linear optical properties can be obtained from the frequency-dependent complex dielectric function ε (ω) (Eq. (2)),

Fig. 5.

	Figure Option ViewDownloadNew Window
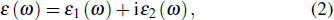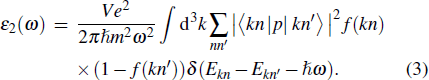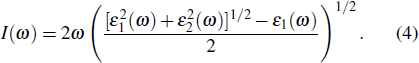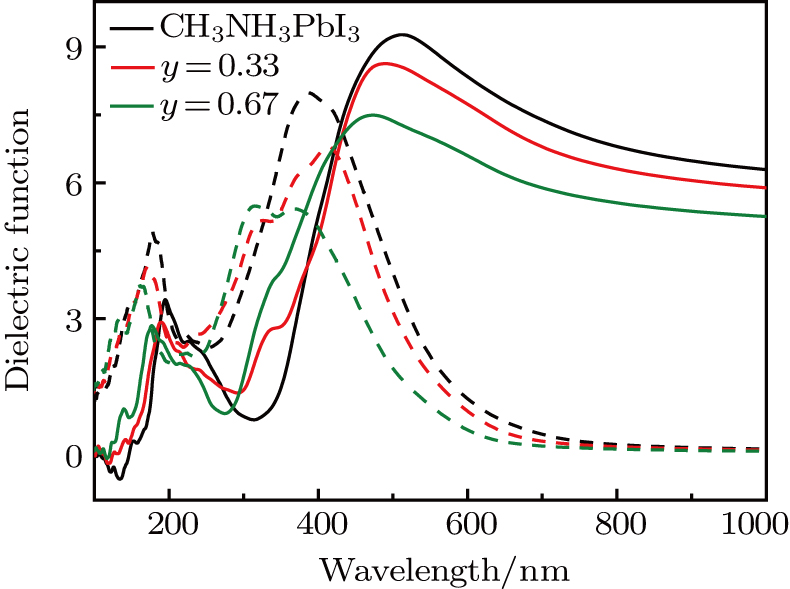	Fig. 5. Real (solid line) and imaginary (dashed line) parts of the dielectric spectra of CH3NH3Pb(I1−yBry)3 (y = 0, 0.33 and 0.67).

As we can clearly see that the doping compounds have a lower computed imaginary part than pure CH₃NH₃PbI₃. The reason for this is that most semiconducting materials have larger band gaps and smaller dielectric constant (Table 1). So, it is not surprising that Cl-doped structure with the band gap of 2.094 eV (y = 0.67) has lower dielectric spectra than Br-doped structure with the band gap of 1.878 eV (y = 0.67). We also note that, for pure and Br-doped concentration reach to y = 0.33, the real part of dielectric function shapes look similar. The phases have positive values in the range of 500 nm to 510 nm. For y = 0.67, the dielectric constants are a little from the other considered compounds, which has smaller dielectric constants. Especially for the results shown in Fig. S8, there is an even lower absorber in the visible light spectrum for Cl-doped reaching to y = 0.67. So, the doping compounds are not better absorbers than the pure ones, and Cl-doped have lower absorption coefficients compared with Br-doped systems. We calculated the absorption spectra of the considered compounds to confirm the conclusion. In Fig. 6, we show absorption spectra for CH₃NH₃Pb(I_1−yBr_y)₃ with y = 0, 0.33, and 0.67. As can be seen from Fig. 6, the absorption spectrum of CH₃NH₃PbI₃ has a distinct absorption band at 350 nm which is highly consistent with previous theoretical data.^[6] We should notice that the absorption coefficient for doping structures are lower than those of CH₃NH₃PbI₃. The optical absorption coefficient is related to the electronic structure, for the Br⁻(Cl⁻) doping system, the band gap is 0.876 eV (0.953 eV) and 0.989 eV (1.126 eV) for y = 0.33 and 0.67, which are both higher than CH₃NH₃PbI₃ (0.793 eV). So, the overall absorption efficiencies of the doping phases are not superior in comparison with the original CH₃NH₃PbI₃ structures in the entire visible spectrum range. The shape of the absorption spectrum becomes narrower as the y value increases. Especially from the calculated Cl-doped absorption coefficient (see Fig. S9), one can see that the absorption coefficients of y = 0.67 are concaved downward to negative values in the 320 nm to 460 nm range. Meanwhile, the curve for CH₃NH₃Pb(I_0.67Cl_0.33)₃ is narrower in comparison with the pure perovskite.

Fig. 6.

	Figure Option ViewDownloadNew Window
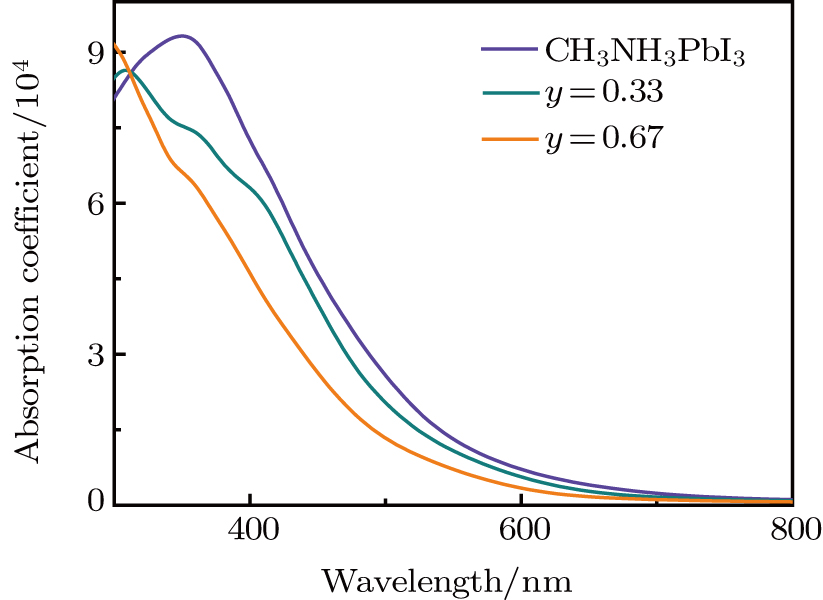	Fig. 6. The absorption spectra of CH3NH3Pb(I1−yBry)3 (y = 0, 0.33 and 0.67) in the visible light spectrum.

Table 1.

Table 1.

Table 1. Calculated band gap (in unit eV) with and without spin–orbital coupling for CH3NH3Pb(I1−yXy)3 (X = Cl, Br; y = 0, 0.33, 0.67) α structures. . CH3NH3PbI3 CH3NH3Pb(I0.67X0.33)3 CH3NH3Pb(I0.33X0.67)3 X = Br X = Cl X = Br X = Cl Band gap (without SOC) 1.711 1.844 1.873 1.878 2.094 Band gap (with SOC) 0.793 0.876 0.953 0.989 1.126

Table 1. Calculated band gap (in unit eV) with and without spin–orbital coupling for CH3NH3Pb(I1−yXy)3 (X = Cl, Br; y = 0, 0.33, 0.67) α structures. .

The Cl-doped structure with the band gap of 1.126 eV (y = 0.67) has a lower absorption coefficient than the Br-doped structure with the band gap of 0.989 eV (y = 0.67) (see Figs. S8–S9 in Appendix A). Moreover, there is a continuous reduction of the absorption spectrum at longer wavelengths as the Cl⁻/Br⁻ doping concentration increases in the compounds. To address the effects of the different site substitution concentration, we consider another two kinds of doping fractions of Cl⁻/Br⁻ (y = 0.33 and 0.67) within the I sublattice (see Fig. S10). For the Br-doped system, when the concentration is up to y = 0.33 and y = 0.67, we consider two kinds of arrangement for the composition to investigate the effect on electronic conductivity, the unique arrangement for y = 0.33 is shown in Fig. S10, namely α and β.

For the Cl-doped system, we consider the same doping concentration and occupation as the Br-doped system. It is interesting to find that when concentration is up to y = 0.33 and y = 0.67, we consider two kinds of site occupation, and obtain the same results for site different occupation position: α and β has the lower optical absorption, respectively (see Figs. S11–S12). As in the above mentioned data, there is the same doping concentration, and the different doping occupation has no influences on the optical properties. So, it is clear that the doping phases are not superior to the pure ones in the entire visible light spectrum but after doping the stability of the material is improving.

In the present paper, a systematic study of the mixed halide CH₃NH₃Pb(I_1−yCl_y)₃ and CH₃NH₃Pb(I_1−yBr_y)₃ perovskites with and without spin–orbit coupling for different y values is carried out by density functional theory calculations. We studied the anionic substitution, which leads to the change of the band gap, density of states, and optical properties of structures. From the calculated band structures and density of states, we can conclude that the considered structures are semiconductors with direct band gaps at the G point and with the increase of doping concentration, the band gap is increased. The band gap is dominated by spin–orbit coupling effects acting mainly on the conduction band. All the considered intensities of the absorption band are decreased, the hybrid perovskites show lower conversion efficiencies than the archetypal halide perovskites. In addition, the Cl-doped structures have smaller lattice distortions and dielectric function in the visible spectrum range in comparison with the Br-doped structures. From the above mentioned results of the high band gap and low absorption efficient, our investigations indicate that Cl/Br-doped perovskites are not good candidates for light materials in solar cells, but after doping the stability of the material improves. The results offer a theoretical foundation for experimental studies of the mixed perovskite and to further explore applications for the other types of materials.