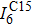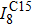† Corresponding author. E-mail:
Molecular dynamics simulations are used to investigate the stabilities of C15 Laves phase structures subjected to temperature and point defects. The simulations based on different empirical potentials show that the bulk perfect C15 Laves phase appears to be stable under a critical temperature in a range from 350 K to 450 K, beyond which it becomes disordered and experiences an abrupt decrement of elastic modulus. In the presence of both vacancy and self-interstitial, the bulk C15 Laves phase becomes unstable at room temperature and prefers to transform into an imperfect body centered cubic (BCC) structure containing free vacancies or vacancy clusters. When a C15 cluster is embedded in BCC iron, the annihilation of interstitials occurs due to the presence of the vacancy, while it exhibits a phase transformation into a (1/2)⟨111⟩ dislocation loop due to the presence of the self-interstitial.
The formation of point defects, e.g., a vacancy and self-interstitial atom (SIA), induced by neutron irradiations in nuclear materials, has been known about for decades. To understand their properties (e.g., the stable state, clustering, and evolution) is a key to studying the radiation damages. For example, the ⟨110⟩ dumbbell in body centered cubic (BCC) iron has been confirmed to be the most stable SIA configuration by the density functional theory (DFT) calculation and experimental measurement,[1,2] while for other BCC transition metals (e.g., tungsten), the ⟨111⟩ crowdion is the most stable self-interstitial state.[3] Because of the high binding energy between SIAs, the SIA-clusters can also form in the atomic displacement cascade and/or the following evolution process of defects. The primary configuration of the SIA-cluster is the dislocation loop, which has been observed with transmission electron microscopy (TEM)[4] and also predicted theoretically by molecular dynamics (MD) calculations.[5,6] The Burgers vector of these loops in BCC iron is either (1/2)⟨111⟩or ⟨100⟩.[6–8] The number ratio between these two loops depends on the irradiation temperature, ion flux, etc.[9] For (1/2)⟨111⟩ loops, MD calculations show that such a loop has lower migration energy and may be absorbed at grain boundaries.[10–12] For the ⟨100⟩ loop, its formation mechanism is one of the recent hot topics and different theories have been suggested accordingly.[11,13,14] Except the dislocation loop, the Bacon group also reported a three-dimensional (3D) metastable sessile di-interstitials structure that has 12 interstitials placed at the edges of a truncated tetrahedron, sharing 10 lattice sites in the irradiated BCC iron, which leads to only two additional atoms in the BCC lattice.[15,16] Such a structure corresponds to the C15 Laves phase.[17] The DFT calculations show that the self-interstitial cluster with C15 Laves phase structure in BCC iron has lower formation energy, higher stability and immobility than the other known SIA-cluster configurations, and can grow by capturing single SIAs.[17] When the number of SIAs is limited, DFT results demonstrate that the tetra- and octa-interstitial clusters with C15 structure have the lowest energy state in all known SIA-cluster configurations in BCC iron.[18,19] MD results showed that C15 clusters can transform into ⟨100⟩ and (1/2)⟨111⟩ loops with a size of 20–30 interstitials.[19] Although the theoretical calculation predicts that C15 clusters form under irradiation, they are rarely observed experimentally.[15–18] Except the susceptibility of the experimental observational technique, there are several factors in the above experimental results: temperature, damage rate, and the effect of point defects, which may affect the lifetime of the C15 phase. In order to provide the possible understanding of the above puzzles, MD simulation is used in this work to explore the stability of the C15 Laves phase, especially to investigate the kinetic properties of the C15 phase at different temperatures. The following factors are mainly studied through MD simulations: 1) the temperature-dependent elastic modulus and structure evolution of perfect C15 Laves iron lattice; 2) structural evolution of C15 Laves iron lattice under the effect of single point defect (SIA or vacancy) at different temperatures, furthermore, for C15 Laves phase cluster embedded in BCC iron; 3) the possible transform driven by point defects and the related critical phase transformation temperature have also been studied. In Section
The A04[20] and M07[13,17] empirical potentials are mainly employed in the present simulations. These potentials are commonly used for studying the radiation damages and have been used in previous studies of the C15 Laves phase.[13,17–19] These previous studies showed that the A04 potential considerably underestimates the stabilities of C15 clusters and the M07 potential slightly overestimates their stabilities in comparison with DFT data.[17] A cubic box with 4 × 4 × 4 unit cells and periodic boundary conditions are used in this work. The size effect is also examined using a larger simulation box (20 × 20 × 20), which shows the same results as those obtained with the small box. The system is relaxed first via molecular statics (MS) simulation, and then MD calculations are carried out with a time-step of 1 fs. Common neighbor analysis (CNA) in OVITO[21] is mainly used to analyze the structural evolution with the temperature dependence and to identify the defects in the BCC and C15 matrix.
After the complete MS relaxations, the formation energy Ef of a single defect is calculated from the following equation:
To study the temperature-dependent structural evolution, the MS and MD simulations are performed alternatively. The structure evolution is visualized using OVITO.[21] After MS relaxation, the system is relaxed with an isothermal–isobaric (NPT) ensemble at each temperature for 100 ps to approach to thermal equilibrium. Further relaxation is performed for 20 ps with a canonical (NVT) ensemble, in which the last 2-ps relaxation results are used for the calculation of the temperature-dependent elastic constants Cijkl following the method developed by Ray et al.[22–24]
It should be noted that the elastic constants calculated from Eq. (
For a perfect C15 Laves phase, its mechanical stability was investigated by analyzing the shear and Young’s moduli versus temperature. The configuration of a unit cell of the C15 Laves phase is provided in Fig.
 | Fig. 1. (color online) Young’s and shear moduli of a perfect C15 Laves phase structure at different temperatures, calculated by A04[20] and M07[13,17] potentials. The enlarged drawing shows the local error bars of temperature-dependent modulus. |
 | Fig. 2. (color online) Snapshots of the evolution of C15 Laves phase calculated by A04 potential[20] from the perfect structure to disordered state. (a) Initial structure relaxed at 0 K; [(b)–(d)] transient states at 400 K, 425 K, and 450 K respectively after MD relaxations. |
Except the effect of temperature on the stability of the perfect C15 Laves phase, the effect of point defects should also be studied because the formation of these defects is inevitable under irradiation in reactors. Based on the calculations of atomic potential energy states, the atoms in the C15 Lave phase are divided into two different atomic sites, thus, resulting in different states of vacancy and SIAs. Type-A atoms located at diamond cubic sites with energy around −4.253 eV by using the A04 potential, and those around −4.534 eV by using the M07 potential are investigated separately. Type-B atoms located at tetrahedral sites with energy around −3.623 eV by using the A04 potential and those around 3.584 eV by using the M07 potential are studied. Thus, the type-A atoms are much more stable than the type-B atoms. By removing a type-A or type-B atom, a single vacancy referred to as A-vac or B-vac is created. By inserting an interstitial around a type-A or type-B atom, a ⟨100⟩, ⟨110⟩ or ⟨111⟩ dumbbell/crowdion is built along one of three coordinate axis directions. It should be noted that configurations of the above dumbbell and crowdion are created just based on previous studies in BCC iron.[1–3] The relaxation may result in different interstitial structures as explained in the following.
The calculation results show that the formation of both type-A and type-B vacancies in a perfect C15 Laves phase can result in the instability of the system. The phase transformation temperatures of C15 calculated by the A04 potential with a type-A vacancy and a type-B vacancy are 260 K and 200 K, respectively. The phase transformation temperatures of C15 calculated by the M07 potential with a type-A vacancy and a type-B vacancy are 290 K and 110 K, respectively. Compared with the results from the phase transformation of the perfect C15 phase as discussed in Subsection
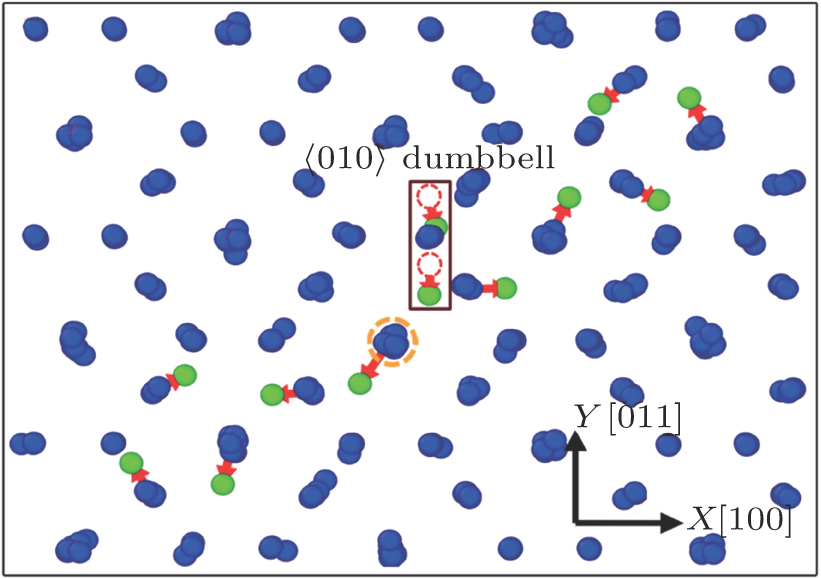 | Fig. 3. (color online) Interstitial structure in C15 Laves phase formed after MS relaxation from the initial ⟨010⟩ dumbbell, calculated with A04 potential.[20] The two red dash circles indicate the positions of the original ⟨010⟩ dumbbell. The red arrow shows the displacement vector of atom from the original (blue spheres) to the final (green spheres) states. |
It is found that all the initial dumbbells or crowdions studied in this work can result in the above structure. The M07 potential is adopted, resulting in a similar state but without showing symmetrical properties. The formation of this structure is also indicated by the displacement vectors of atoms as shown in the figure, where one atom of the dumbbell moves back to the mass center of the dumbbell, forcing another atom of the dumbbell to move away from its original position, leading to a series of atom displacements and the formation of such a symmetrical defect structure (Fig.
After the phase transformation from C15 to the disordered state due to the temperature change or the appearance of defects, long time MD simulations also indicate that the further phase transformation from the disordered state to a BCC lattice state can also occur. The structure evolution process of C15 with a type-A vacancy or a type-A ⟨010⟩ dumbbell at 300 K simulated by A04 and M07 potential are similar as shown by the examples in Fig.
 | Fig. 4. (color online) Phase transformations of C15 Laves phase containing (a) a vacancy and (b) an SIA, calculated with the A04 potential.[20] Atomic projections are on the basal (XY) plane. [(a1) and (b1)] Initial states after relaxation at time zero. [(a2)–(a4)] and [(b2)–(b4)] Structural evolutions at 300 K, (a4) and (b4) final BCC lattice structures containing vacancies or vacancy clusters. |
In the present work, in order to understand the temperature-dependent stability of the C15 Laves phase cluster embedded in the BCC iron, the BCC iron simulation box with 30 × 30 × 30 unit cells containing a C15 cluster with two interstitials up to tens of interstitials is built for MD simulations at different temperatures. The C15 clusters can spontaneously transform into an SIA-cluster composed of the parallel ⟨111⟩ crowdions or loops, depending on the critical temperatures and the size of the C15 clusters (see Table
| Table 1.
The phase transformation temperature of a C15 cluster containing di-interstitial to deca-interstitial. . |
Considering the radiation environment, the influences of the additional vacancy and interstitial on the stability of the C15 Laves phase in BCC iron are also studied. As an example, the 




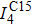

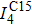

 | Fig. 5. (color online) Phase transformation processes at 300 K for an 
|
The effects of point defects and temperature on the stability of the C15 Laves phase structure of Fe have been investigated via the molecular dynamic simulations. A bulk perfect C15 Laves phase is stable at room temperature, and it exhibits a phase transformation into a BCC lattice structure with increasing temperature in a range of 350 K–450 K, depending on the employed interatomic potentials. The presence of a single point defect reduces the temperature of such a phase transformation. For a C15 cluster embedded in Fe, the spontaneous transformations occur at the critical C15 size with around 2–8 interstitials. The presence of both vacancy and interstitial in the vicinity of a C15 cluster can result in its phase transformation through either the annihilation of interstitials in the C15 phase or the formation of a (1/2)⟨111⟩ dislocation loop, depending on the critical temperature and the number of added point defects. Therefore, considering the harsh environment (e.g., high temperatures, supersaturated interstitials and vacancies) in nuclear reactors, the C15 Laves phase may exist in a visible period during irradiation, but it has rarely been observed with transmission electron microscopy measurement.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] |