† Corresponding author. E-mail:
By minimizing the enthalpy of packings of frictionless particles, we obtain jammed solids at desired pressures and hence investigate the jamming transition with and without shear. Typical scaling relations of the jamming transition are recovered in both cases. In contrast to systems without shear, shear-driven jamming transition occurs at a higher packing fraction and the jammed solids are more rigid with an anisotropic force network. Furthermore, by introducing the macrofriction coefficient, we propose an explanation of the packing fraction gap between sheared and non-sheared systems at fixed pressure.
Jamming transition occurs when a system undergoes the transition from a liquid-like state to a rigid but disordered solid state, which is widely studied in dense disordered systems of colloids, emulsions, foams, and granular materials.[1–5] At zero temperature (T = 0) and driven by the increase of packing fraction, packings of frictionless particles obtained by fast quench of random configurations jam at a critical-like point called point J associated with a critical packing fraction ϕJ.[2,6–11] Marginally jammed solids right above ϕJ exhibit specific scaling behaviors.[12–19] Despite recent efforts, a full understanding of the jamming transition is still lacking.
It has been shown that the jamming transition threshold ϕJ is well-defined and corresponds to the random close packing of hard spheres for fast quenched systems.[2,3,6,8,19–22] However, the uniqueness of ϕJ has been questioned by recent studies of the protocol dependence of the jamming transition. It has been illustrated that amorphous, isostatic packings of frictionless spheres can exist over a finite range of packing fractions, with rather weak correlations between structural order and packing fraction, which extend the jamming transition from a jamming point to a jamming line.[23–34]
Among the studies of protocol dependence of ϕJ, what interests us here is the observations of the ϕJ increase for packings of frictionless particles under load such as shear[9,19,27] or self propulsion.[21] A superficial guess of such ϕJ increase may be the presence of a non-zero shear stress or particle activity. It is however interesting to know whether the increase reflects some inherent properties of jammed solids. A jammed solid has a non-zero pressure and yield stress.[7,19,35] Under quasistatic planar shear, it deforms elastically under small shear strains and flows when the shear stress exceeds the yield stress. This is analogical to the stick-slip motion of a pushed object on a rough surface, which implies the existence of an effective macro-friction.[36–38] By definition, the macro-friction coefficient is equal to the ratio of the yield shear stress to the pressure. We are interested to see whether the ϕJ increase of sheared systems is related to the macro-friction.
Different from previous approaches to minimize the potential energy at a fixed packing fraction, here we simply minimize the enthalpy to quickly obtain jammed solids at desired pressures. Because the packing fraction is allowed to vary during minimization, our jammed solids are stable subject to the change of packing fraction.[39] We explore marginally jammed solids under fixed pressure with and without shear and reproduce well-known critical scalings of the jamming transition. Possibly due to the new minimization method, we obtain a slightly different finite size scaling exponent of ϕJ from previous approaches. With shear, ϕJ is higher than that without shear, as expected, and the jammed solids are more rigid and anisotropic in force network. Furthermore, we find a roughly linear correlation between the macro-friction and the packing fraction gap between sheared and non-sheared solids under the same pressure. We thus propose that the increase of ϕJ under shear results from the macro-friction.
To avoid crystallization, we put N/2 large and N/2 small disks with equal mass m into a box with side length L. The diameter ratio of the large to small particles is 1.4. The interparticle potential is[2,19,40,41]
To reduce the fuzziness of the packing fraction in quantifying the distance to the jamming transition due to the finite size effect, we choose here the pressure as the control parameter. Under constant pressure condition, enthalpy is the right characteristic energy insted of the potential energy. We thus generate static packings at fixed pressure p by applying the fast inertial relaxation engine method[42] to minimize the enthalpy H = U + pV of random configurations, where U = ΣijU(rij) is the sum of potential energy over all pairs of particles and V = Ld is the volume with d being the dimension of space. Without shear, we apply periodic boundary conditions in all direction. To realize quasistatic shear, we successively increase the shear strain γ by a small increment δγ, followed by the minimization of the enthalpy under the Lees–Edwards boundary conditions.[43] In this work, we show results for two-dimensional (d = 2) systems with harmonic repulsion (α = 2). We vary the system size N from 64 to 8192.
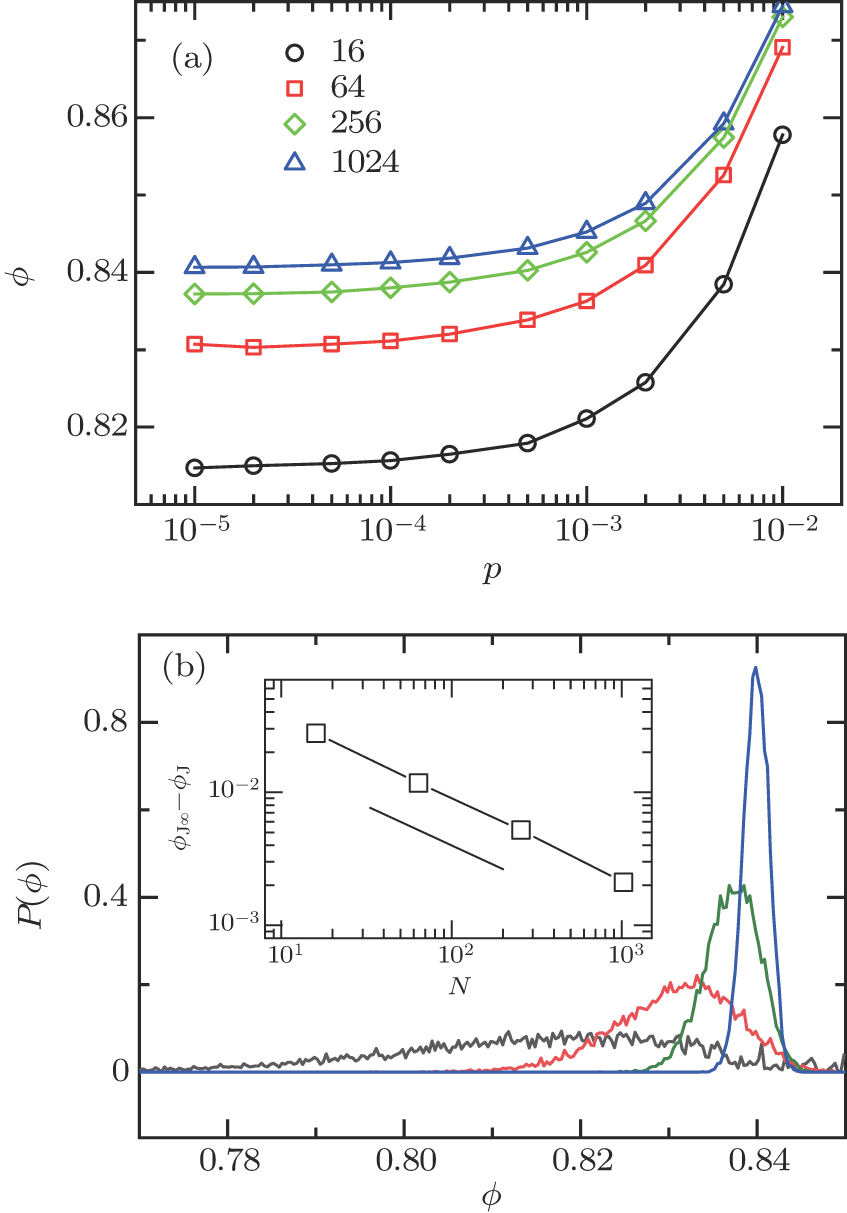
Figure
In Fig.
The inset of Fig.
In Fig. 
To illustrate that the gap 
We have shown that ϕ(p) for both sheared and non-sheared systems exhibit the same type of scaling. In Fig.
As compared by Figs.
In order to quantify the bond anisotropy, we plot in Fig.
As mentioned earlier, the response of a jammed solid to the quasistatic planar shear is analogical to that of an object on a frictional surface to a push or drag. It is thus natural to expect that the macro-friction is essential to some behaviors of jammed solids under shear, including the increase of the jamming transition threshold discussed in Subsection
Interestingly, when we plot the packing fraction gap Δϕ between sheared and non-sheared systems against the macro-friction coefficient for all pressures studied, as shown in Fig.
The sheared solids concerned here have nonzero shear stresses fluctuating around the yield stress. If the macro-friction were zero, the yield stress would vanish and applying shear deformation would not affect jammed solids. When μ increases, the difference induced by shear would grow. Therefore, it is expected that Δϕ increases with increasing μ. Approaching the unjamming transition, both the pressure and yield stress approach zero, but their ratio remains almost constant. It is thus the macro-friction but not the shear stress that plays the key role in determining the response ability of marginally jammed solids to shear, particularly non-vanishing ΔϕJ observed here.
By performing the minimization of enthalpy, we obtain marginally jammed solids under constant pressure and compare the jamming transition and properties of marginally jammed solids with and without shear. The new minimization approach excludes unstable states subject to the change of packing fraction, but the well-known scaling relations obtained by potential energy minimization under constant packing fraction are still recovered, except that here we achieve a slightly smaller finite size scaling exponent of the jamming transition threshold. When shear is applied, the jamming transition is pushed to a higher packing fraction and the jammed solids are more rigid with a larger shear modulus. Our analysis attributes the increase of the jamming transition threshold to the existence of nonzero macro-friction and the enhancement of the rigidity to the anisotropic angle distribution of strong bonds.
The macro-friction comes from disordered structures of jammed solids. We have proposed to use it to explain the shear-induced increase of the jamming transition threshold. Moreover, previous studies have shown that the yield stress of marginally jammed solids decreases with increasing system size.[19] By definition, the macro-friction also decreases when system size increases. From our analysis, the gap of the jamming transition thresholds between sheared and non-sheared systems should decrease as well, which is exactly what we observe in Fig.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] |