1. IntroductionThe transition from L-mode to H-mode was discovered in 1982 at neutral-injection-heated ASDEX divertor discharges.[1] The H-mode is a high confinement mode in the plasma characterized by higher energy and particle confinement than L-mode,[2] which makes the fusion reaction possible. In the L-mode, the plasma transport increases gradually with the power inputs. When the input energy exceed a threshold value, a transport barrier takes place at the edge of the plasma, which indicates the LH transition.[3] Meanwhile, more recent researches have focused on the state characterized by an intermediate oscillatory between L- and H-modes, termed as I-phase.[4,5] Confinement regimes correspond to the states of turbulence, because the performance of a fusion reactor is strongly influenced by the turbulent transport.[6] In order to study the nonlinear mechanism associated with the LH transition, lots of theoretical and experimental efforts have been made, which revealed that the zonal flows play a key role in the drift wave turbulence,[6,7] mean E × B flow will suppress the turbulence,[8,9] and different types of transitions (such as oscillating, sharp and smooth ones) are also discovered.[10,11]
The active studies in this field are aimed at an understanding of nonlinear physics processes in coherent structure formation and anomalous transport in plasmas.[12] The importance of zonal flows in the LH transition was experimentally demonstrated through bicoherence analysis on DIII-D experimental data.[13] The authors in Ref. [6] proposed a self-consistent 0D model for the LH transition and demonstrated that the zonal flow self-generates with the growing of turbulence by the pressure gradient. After that zonal flow and turbulence entered into a self-regulating regime, where self-organization takes place using the nonlinear signal processing technique.[14] Sheared flows excited by turbulence was dealt with by the three-wave interactions theory.[15] Three-wave interactions between small scale high-frequency turbulence and larger scale lower-frequency fluctuations increase transiently during the transition from low to high confinement regime.[14] It is captured that energy transfer among three waves plays a key role.[16] The effect of energy transfer between turbulence and the zonal flow was observed in an LCO, where the zonal flow is estimated by the amplitude fluctuating of the radial electric field, and the ambient turbulence energy is measured by the electrons density fluctuations.[17] LCO was also used to analyze the dynamics of turbulence and the coherent structure in the transition,[18] but the detailed dynamic features of the LCOs, consisting of causality and conditions for the different instruments have not been identified. Experiments on the HL-2A tokamak studied the dynamic features in the LH transition, which showed that there are two different types of limit cycle, and reported the mechanism of zonal flow and pressure gradient induced shear flow in suppressing turbulence and the converting from type-Y LCO to the type-J one.[19] Energy transfer from the turbulence to large-scale axisymmetric flows has been quantified in L-LCO and fast LH transition in several devices.[20] These results clarified the essential evolution of the turbulence, zonal flow, shear flow, and ion-pressure gradient during LH transition. However, the nonlinear dynamics, the underlying physics of the interaction among these waves, and the key variables which determine the LH transition have not emerged yet.[3] Without doubt, figuring out the transition physics is not only fundamental for assessing the power threshold scaling and ensuring heating requirements for future fusion reactors, but also help in discussing the nonlinear evolution of the linear unstable mode.
In this paper, the transition dynamics of low-I phase-high (LIH) confinement state is studied in detail by numerical simulations, where I-phase here is the interim before the system enters into H-mode, which is different from I-mode in Ref. [21]. The rest of this paper is organized as follows. In Section 2, three-wave coupling theory is introduced and extended to investigate the nonlinear dynamics of the LIH transition for the first time, which is clarified to be suitable for studying unstable waves,[22–24] where turbulence is decomposed into a PF wave and an NF one according to their linear frequency. After that, the evolution of PF wave, NF wave, ZF, and the pressure gradient, on account of their amplitudes and phases are illustrated in Section 3. Different stages of LCOs with reversed rotation direction during the LIH transition are also shown. Finally Section 4 gives a summary and an outlook.
2. Three-wave coupling modelThe wave-wave interaction is the basic process of energy transfer among nonlinear wave coupling modes. The nonlinear wave system can start from one mode and then excite more and more modes. In general, in regard to the wave system which consists of quadratic nonlinear terms, when the three modes satisfy k1 + k2 + k3 = 0,[25] they can be three resonant waves.[26] Then if neglecting the contribution of other modes and considering the three main modes, a closed loop can be obtained with truncating the three waves in resonance modes. Starting from the conservative nonlinear drift wave which propagates in a plane perpendicular to the magnetic field, a simplified three-wave model is established, which is an integrable Hamiltonian system.[25] For nonlinear drift wave equations, the mode-coupling mechanism may be caused by the convection of E × B from density fluctuation, ion inertia or polarization drift. Either of these nonlinear mechanisms, as well as other E × B convective nonlinear coupling mechanisms, may be incorporated into the general drift-wave equation.
Our model is based on the Hasegawa–Mima equation which eliminates the nonlinear term because of the plasma temperature gradient. Let us start from the Hasegawa–Mima equation for a nonlinear drift-wave.
which describes the evolution of the fluctuating electric potential
ϕ caused by the drift of charged particles in the inhomogeneous magnetized plasma with the density gradient.
is the mixed derivative term originating from polarization drift, and
∂ϕ/
∂y comes from the
E ×
B drift wave,
vd is the drift speed. Here the Fourier modes of the fluctuation field are defined through the complex amplitude
ϕ(
x,
t) = Σ
ϕk(
t)e
ik·x.
[22] According to
, assuming that boundary periodic condition is
ϕ(
x + 2
π) =
ϕ(
x), wave vectors
m,
n is taken as integer values as the index of
k, which is used for solving the revolution of
ϕk. Multiplying both sides of Eq. (
1) with e
−ik′·x, then integrating
x from 0 to 2
π, the evolution of
ϕk(
t) is obtained
where
k⊥ and
ky are projections respectively onto a plane or on the
y direction perpendicular to the magnetic field. The system energy is integrated by
W = (1/2)∫[
ϕ2 + (∇
⊥ϕ)
2]d
x,
[22] and it is easy to verify d
W/d
t = 0, which makes the system a conservative one. Truncating Eq. (
2) to satisfy the resonance condition
k1 +
k2 +
k3 = 0, the general model of three-wave dynamics in a conservative system is deduced to a simplified form
where
j,
l,
m are cyclic permutations of 1, 2, 3 and
is the linear oscillating frequency of the mode whose wave number is
kj.
is the complex conjugate of mode
ϕj. The nonlinear coefficient
A = (1/2)
z ·
kl ×
km is a compassed triangle area of three-wave vector, which determines the strength of the three-wave coupling interaction.
satisfies Σ
Fj = 0, which ensures that the nonlinear terms would not cause the dissipation or increment of the overall energy. The simplified three-wave equation makes sure that each
ϕj oscillates with a linear frequency
ωj, and energy will also exchange among these three waves.
in Eq. (
1) comes from the polarization drift, which affects the dispersion behavior of the system, and the group velocity of small scale structure is limited. So the contribution of
is included only via modified linear frequencies in Eq. (
3). In this three-wave model, we do not care about the spatial structure formation of the fluctuation but instead the time evolution of the waves. When discussing the nonlinear drift wave with dissipation, it needs to consider that the electron density is not adiabatic to the fluctuation of the electric field. Thus it is reasonable to assume that one mode grows exponentially because of linear instability, the other two modes decay exponentially because of the dissipation. Substitute the complex amplitude
ϕj(
t) as
ϕj(
t) =
aj(
t)exp[i
αj(
t)] with the real amplitude
aj(
t) and the real phase
αj(
t).
[22] Let us plug
ϕj(
t) =
aj(
t)exp[i
αj(
t)] into Eq. (
3) and separate the real part and imaginary part in the equation. Then we can obtain six nonlinear coupling equations about
aj(
t) and
αj(
t)
By substituting
α(
t) =
α1 (
t) +
α2 (
t) +
α3 (
t), equations (
4) and (
5) can be simplified as follows:
where Δ
ω = Σ
jωj is the frequency mismatching of the three resonance modes. The three-wave system of Eqs. (
4) and (
5) is conservative because the time derivative of the system energy d
W/d
t = 0. But as a matter of fact, the wave–wave system is not conservative because of the linear instability, the outsider driver or the energy loss. For a detailed study of the dynamics of the turbulence here, it is needed to consider the non-adiabatic electron density. The integrated three-wave system becomes
where
j = 1, 2, 3. Presume that one mode
k = 1 grows, that is,
γ1 > 0, and the other two modes
k = 2, 3 damps, that is,
γ2 < 0,
γ3 < 0. The choice of
Gj is the same as
Fj, satisfying Σ
Gj = 0, which makes sure the nonlinear terms in the equations would not cause the gain or loss on the whole system energy.
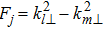
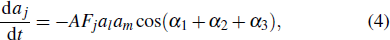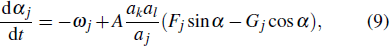Based on the above three-wave coupling model, we take the two basic modes of the turbulence, which is a positive frequency (PF) part with amplitude ε+, phase α+, and a negative frequency (NF) one with amplitude ε−, phase α−, according to their linear frequency. The perturbation of the nonlinear eigenfrequency propagating forward and backward in the nonlinear system can make the positive energy mode and negative energy mode, and the frequency of the mode can be used to describe the turbulence.[27] The amplitude of ZF is VZF, and the phase of ZF is αZF. The pressure gradient N added here is the power source, which is the control quantity of PF, NF, and ZF. We assume that the PF mode increases linearly as a pump wave, the other two NF modes and the zonal flow damp linearly according to the driven-damped three-wave function.[28] Then the extended three-wave equation becomes
 | |
 | |
 | |
 | |
 | |
 | |
 | |
To concern the nonlinear interactions of PF turbulence, NF one, ZF, and pressure gradient as many as possible, the driving and dissipation terms are added phenomenologically, where ai, bi, ci, and di are parameters of the interaction strength and the exact values of them are not sensitive to the qualitative discussion here. For example, equation (10) describes the amplitude of PF, where the first term on the right-hand side of the equation originates from the theory of the three-wave interaction, the second term represents its generation by pressure gradient via linear instability, the third one is the nonlinear saturation of the PF turbulence, and the rest of the terms are the shear suppression of turbulence by mean E × B flows (which influences the system, but we do not concentrate on it here) according to the approximation to the ion momentum balance equation as N2 and the dissipation by ZF, respectively.[7] Equation (16) is the evolution of the pressure gradient N, which is related to the input power Q, where the high order term describes the interaction of the turbulence and ZF on the pressure.
3. Numerical simulationBy solving Eqs. (10)–(16) numerically, the dynamics of the LH confinement transition and the interaction among turbulence, ZF, and pressure gradient can be obtained. The parameters in the following are chosen as an example: the positive frequency ω1 = 3.0, the negative frequency ω2 = −3.0, ωZF = 0.01, the strength of the interaction A = 2.0, and vectors F1 = 3.0, F2 = −2.9, F3 = −0.1, G1 = 3.0, G2 = −2.9, G3 = −0.1. It is verified that the results presented here can be observed in a broad parameter region.
The three stages of the LIH transition divided with a solid line can be clearly seen from Fig. 1. The first stage is the L confinement mode. At the L mode, when N becomes sufficiently high as a result of continuous increasing input power Q, a portion of energy transfers to turbulence, thus the PF wave is excited firstly. Actually, at the same time, ZF is also excited together with NF, just like fluctuation, because of the small amplitudes of them. The second stage is the I-phase, which just means an intermediate process between L-mode and H-mode as discussed in Ref. [19], where the NF wave is excited and grows directly. ZF emerges in no time after turbulence begins to fluctuate. In the I-phase state, the waves self-regulate via the three-wave coupling mechanism. From the marked dash line, it can be seen that when ε+ oscillates to the peak point, ε− and VZF reach the valley, whereas when ε− and VZF oscillate to the peak point, ε+ reaches the valley. In the last stage, it is seen that the decay of the zonal flow leads the system to the H mode. NF ε− directly damps while the PF ε+ still increases a little bit before decreasing to zero. The pressure gradient N keeps growing because of the continuous input energy.
In order to deeply figure out the mechanism of the LH mode transition, some researches focused on the dynamics of LCO near the transition boundary in the I-phase.[17,19,20] The authors in Ref. [19] found two different rotations in the I-phase. Our simulation shows that there are also three stages of LCOs with reversed rotation direction according to that of the LIH confinement transition.
Figure 2 shows the LCOs of ε+ versus N, where the parameters are the same as before. Panel (a) is LCO in the L confinement mode, while panels (b) and (c) are LCOs in the I-phase and the H mode respectively. It is obvious that the rotation direction changes during the LIH transition. The energy transfer and competition between the PF turbulence and the pressure gradient N are illustrated too. Looking into the LCO in panel (a) when the system stays in the L mode, the rotation is anticlockwise. The PF turbulence ε+ grows first, causing the reduction of fluctuation of the pressure gradient N. As the system begins to regulate itself, it enters into the I phase plotted in panel (b), the rotation of the LCO reverses to clockwise. The pressure gradient N grows first, followed by the increasing of the localized flow, including PF, NF, and ZF, which ensures the system develops through the nonlinear interaction. At last, as it transits into the H mode, the rotation of the LCO reverses again back to anticlockwise, the same as the L mode, but it does not keep a long time because the turbulence damps to zero rapidly. It is worth while mentioning that the three stages of the LCO dynamics and the energy exchange implied from these results are in agreement with Fig. 1.
Another perspective to study the nonlinear mechanism of the LIH transition is the wave phases because they play an important role especially in the coupling wave–wave interaction. Cosine of α+ and α− during the LIH transition are shown in Fig. 3. Here the parameters for panels (a), (b), and (c) are the same as those taken in Fig. 1. Correspondingly, the three stages of the whole transition process can be obviously distinguished. At the beginning of the evolution, that is, the L mode, as shown in the forepart of panel (a), cosα+ is ahead of cosα−, which means that the phase of the PF turbulence leads that of the NF one. Then in the I-phase the two phases begin to modulate themselves, presented in the rear of panels (a),(b), and the forepart of panel (c). After the self-regulate process finishes, it transits back, as shown in the rear of panel (c), where cosα+ is ahead of cosα− again. The first turning point is about Q = 0.55 and the second one is about Q = 1.01, which is in agreement with the reversal of the rotation of LCOs as shown in Fig. 2, as well as the transition point from L- to I-phase and I-phase to H-phase respectively, as shown in Fig. 1. Thus, the evolution of the wave phases can be regarded as one of the mechanisms of LIH transition and the reversed rotation of LCOs.
4. ConclusionIn summary, in order to figure out the dynamics of the LIH transition, the extended three-wave coupling model is introduced here to describe the interactions of PF turbulence, NF one, ZF, and pressure gradient. The LIH transition is found in a broad parameter regime, accompanied with the energy exchange. In L-mode, pressure N increases at first with the energy input, then PF turbulence arises. In I-phase, NF turbulence and ZF emerge and oscillate together with the PF wave. When PF turbulence, NF one, and ZF all decent rapidly to almost zero, it transits to H-mode. Afterwards, it is found that there are different reversed rotation directions of LCO in three stages too. The LCO of the amplitude of the PF turbulence ε+ and pressure gradient N rotates anticlockwise in the L and H modes, while in the I-phase, it rotates clockwise reversely. Further, it is found that in the L and H mode, cosα+ is ahead of cosα−, which implies that the phase of the PF turbulence leads that of the NF one. While in the I-phase, the phases are self-regulating. The turning points of the input power Q for wave phases is in agreement with that for the LIH transition, which illustrates that the evolution of the wave phases is responsible for the LIH transition and the reversed rotation of LCOs.
However, additional work is needed to definitively demonstrate the formation of the spatial structure of the fluctuation during the LH transition, which might be the limitation of the three-wave interaction model.
