Project supported by the National Key Research and Development Program of China (Grant No. 2017YFA0304401), the National Development Project for Major Scientific Research Facility, China (Grant No. ZDYZ2012-2), the National Natural Science Foundation of China (Grant Nos. 91336211 11634013, 11474318, and 11622434), the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB21030100), the Hubei Provincial Science Fund for Distinguished Young Scholars, China (Grant No. 2017CFA040), and the Youth Innovation Promotion Association, Chinese Academy of Sciences (Grant No. 2015274).
Project supported by the National Key Research and Development Program of China (Grant No. 2017YFA0304401), the National Development Project for Major Scientific Research Facility, China (Grant No. ZDYZ2012-2), the National Natural Science Foundation of China (Grant Nos. 91336211 11634013, 11474318, and 11622434), the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB21030100), the Hubei Provincial Science Fund for Distinguished Young Scholars, China (Grant No. 2017CFA040), and the Youth Innovation Promotion Association, Chinese Academy of Sciences (Grant No. 2015274).
† Corresponding author. E-mail:
Project supported by the National Key Research and Development Program of China (Grant No. 2017YFA0304401), the National Development Project for Major Scientific Research Facility, China (Grant No. ZDYZ2012-2), the National Natural Science Foundation of China (Grant Nos. 91336211 11634013, 11474318, and 11622434), the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB21030100), the Hubei Provincial Science Fund for Distinguished Young Scholars, China (Grant No. 2017CFA040), and the Youth Innovation Promotion Association, Chinese Academy of Sciences (Grant No. 2015274).
Potential distribution is an important characteristic for evaluating the performance of an ion trap. Here, we analyze and optimize the potential distribution of an endcap ion trap for single-ion trapping. We obtain an optimal endcap radius of 225 μm–250 μm, endcap-shield gap of ∼ 250 μm, and inter-endcap distance of 540 μm–590 μm. The simulation method for analysis can also be applied to other ion traps, which is useful for improving the design and assembly of ion traps.
Ions trapped and laser-cooled in the radio-frequency (RF) field have been widely used in some areas, such as optical frequency standards (OFSs),[1–7] quantum information processing,[8–13] and quantum simulations.[14–17] In these applications, the structure of the ion trap is an important determinant of the ion trapping performance. For OFS applications, micro-motion is one of the main sources of system shifts, and it mainly depends on the trap parameters and assembly. Thus, it is very important to choose a suitable trap structure and parameters.[18] The endcap Paul trap is very suitable for single-ion trapping, because it has an open structure that enables laser access, its microscopic geometric structure is quite elaborate, and the fabrication process is relatively simple.
In the present work, we choose the endcap trap that was first proposed by Schrama et al.[19] with different geometric variants of the conventional quadrupole potential. We build a model of the endcap trap by using the commercial software COMSOL Multiphysics, simulate the potential distribution by using the finite element method, and derive optimal parameters. The main parameters of the physical model are adjusted to achieve the optimal manipulation of single ions. The trajectory of Sr+ ions is then simulated, from which the secular motion and micro-motion frequency are predicted. The simulated results are compared with the experimental results obtained at the National Physical Laboratory (NPL).[20] Finally, the motion of a single Ca+ ion, trapped in our vacuum chamber at a pressure of ∼ 10−8 Pa, can be simulated using our endcap trap model. The simulation results are used as a reference to study a directly laser-cooled Al+ optical clock, which we are planning to build in the very near future; the current endcap trap model is envisioned to be a critical component of that future system.
In an ion trap, the motion of a charged particle is limited by electric and magnetic fields. Ion traps can be divided into two main types, depending on the nature of the trapping field. One type is the Penning trap, which traps ions by using static electric and magnetic fields.[21] The other is the Paul trap, which traps ions by using RF alternating current (AC) electric potential fields at a level of a few megahertz.[22] The function of the Paul trap is determined by its structure. In this work, we focus on the endcap trap that is used primarily for trapping single ions, which is suitable for our experiments on the direct cooling of aluminum ions. As shown in Fig.
 | Fig. 1. (color online) (a) Photograph of the endcap used in our laboratory, and (b) potential distribution around the center of endcap. |
Earnshaw’s theorem states that a collection of point charges cannot be maintained in a stable stationary equilibrium configuration solely by electrostatic interactions between the charges.[23] Thus, it is necessary to add an AC electric field on the electrodes:
The trap has rotational symmetry about the z axis, thus, the potential does not rely on angle φ.
When expressed in polar coordinates, the potential at the point (r, z) is given by[14]
Taking n values of 2 to 6, we obtain
As we mentioned above, the endcap trap possesses rotational symmetry about the z axis. The ion has the same motion trajectory at any arbitrary plane along the z axis. The ion motion can be confined roughly in a two-dimensional (2D) plane. At this point, the simulation can be simplified without affecting the results. After building the geometric model, a corresponding voltage is applied to the resulting trap model.
The geometric structure of the endcap trap is shown in Fig.
Before simulating the trap’s potential, a test simulation was conducted to probe the performance of the software. A parallel capacitor was considered by using the software as shown in Fig.
 | Fig. 3. (color online) Graphical presentation of the simulation of the Ca+ ion’s motion in planar plate capacitor. |
The most important part of the simulation is mesh division, the quality of which is limited by our computing capability. Using COMSOL and MATLAB, we can also precisely control each mesh node and assess the details of the mesh quality distribution. The average statistical mesh quality was 0.97, initially at 0.85. We also built some mesh-controlled virtual geometry near the saddle point, where ions generally remained, to increase the resolution of the mesh. This procedure is advantageous for mesh division and does not affect the results of simulation.
Next, the parameters were optimized.
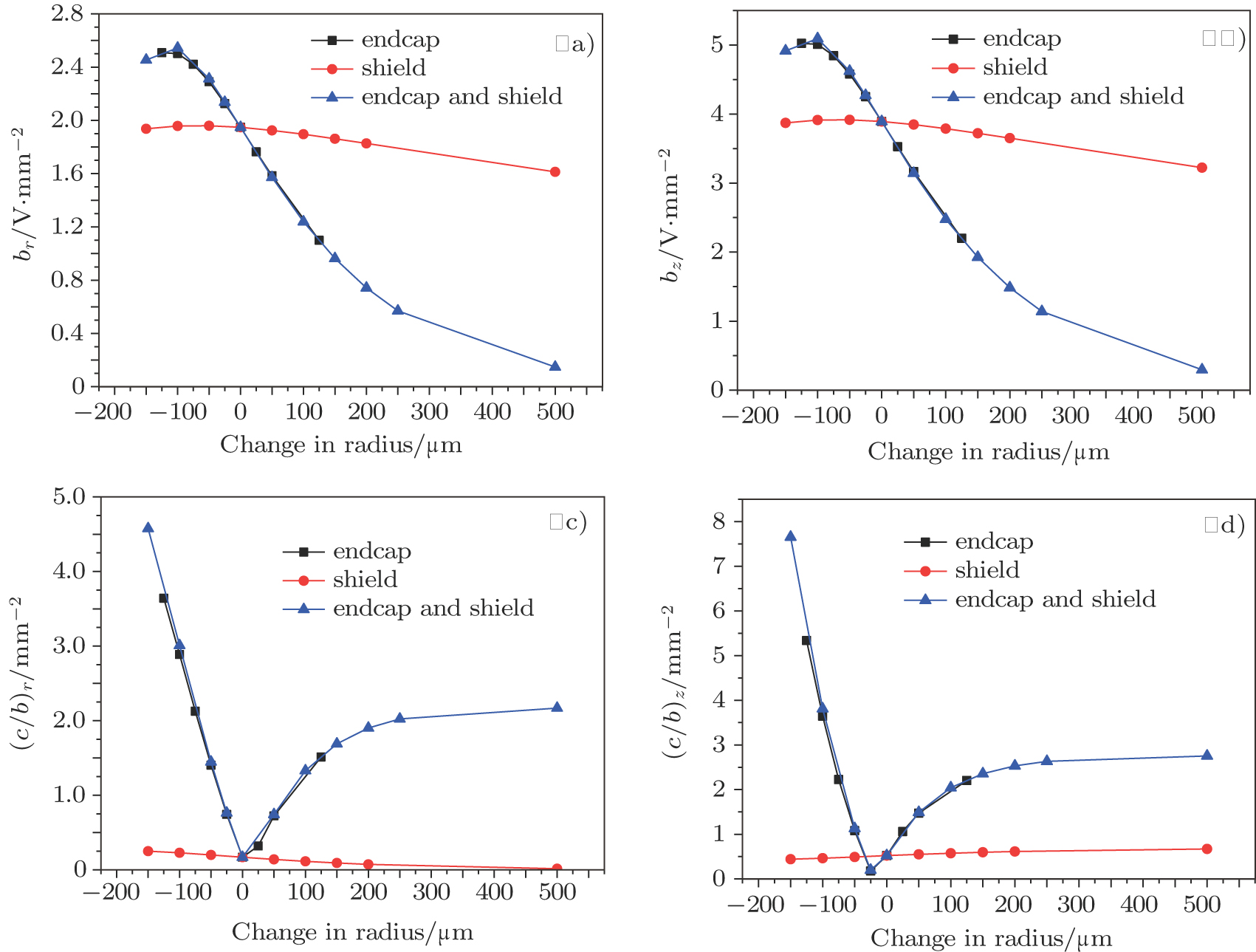
First, the radius of the device was varied. We changed r1 alone, r2 alone, and r1 and r2 simultaneously. The initial radius of the endcap, r1, was set to be 250 μm, and the initial radius of the shield surrounding the endcap, r2, was set to be 500 μm. We varied r1 from 125 μm to 375 μm in steps of 25 μm, and we varied r2 from 350 μm to 700 μm; further, 1000 μm was set as a far point, for examining a relatively extreme situation. In Fig.
Second, the distances from the trap center to the endcap tip and from the trap center to the shield tip were varied. Three situations were considered: 1) moving only the endcap, 2) moving only the shield, and 3) moving the endcap and the shield simultaneously. By analyzing the results, the range of distances by which the two components of the trap should be separated was determined.
Figure
 | Fig. 5. (color online) Plots of (a) trap depth and (b) anharmonic coefficient versus distance upper endcap moves for various endcap locations. |
Figure
 | Fig. 6. (color online) Curves of (a) trap depth and (b) anharmonic coefficient versus distance endcap moves from center. |
We obtained optimized trap parameters from the simulation. Based on the simulation, for optimal performance the radius of the endcap should be in the range of 225 μm–250 μm. Further, the gap between the endcap and the shield should be kept at ∼ 250 μm. In addition, the distance between the two endcaps should be in the range of 540 μm–590 μm.
Imperfections were also considered, such as the rotation of the endcaps at a specific angle with respect to the z direction, a shift of the endcap away from the trap axis, and the replacement of the mirror surface of the endcaps with a triangular wave, hollow semicircle, or nipple. The result for an imperfect endcap trap shows that the ratio c/b changes little compared with that for the flawless trap, but the effect is not negligible.
For comparison, experimental data from NPL were used in the ion trajectory simulation. The RF voltage was set to be 199 V (rms), and the frequency was set to be 15.955 MHz. The DC voltage applied to the shield was 2.12 V. The endcaps each with a radius of 250 μm were separated by 560 μm. The shields were separated by 1 mm and angled at 45° with respect to the trap axis. An 88Sr+ ion was loaded with an initial kinetic energy of 0.05 eV from the center of the trap, with its velocity direction chosen randomly. The COMSOL has a particular particle trajectory node that is used to simulate the motion of charged particles in magnetic and electric fields. Another three-dimensional (3D) model was built in COMSOL by using the above parameters for a particle trajectory node. The motion data were exported and organized to calculate the secular frequencies. The secular frequencies were calculated to be 1.406 MHz in the r direction and 2.907 MHz in the z direction respectively, which were in good agreement with the NPL experimental results.[20]
In this work, an AC model has been used to simulate the endcap in the Paul trap, and the optimal trap parameters have been obtained. According to our results, the radius of the endcap should be in the range of 225 μm–250 μm, and the gap between the endcap and the shield should be ∼ 250 μm. Further, the distance between the two endcaps should be in the range of 540 μm–590 μm. These theoretical results can be used to guide experiments; for example, for designing the Ca+ ion optical clock that we are currently developing, and for designing a directly laser-cooled Al+ optical clock that we are to build in the near future. Further, the module can be used to determine the scale of the voltage applied to the compensation electrode to provide the ions with better trapping conditions. As COMSOL can also simulate the laser, it will be feasible in the next step to simulate the Doppler cooling of ions in the trap if we can build a two-level energy state model of the trapped ion. This function is not yet supported by the COMSOL module; however, we can formulate its associated partial differential equation by using COMSOL or MATLAB script. Furthermore, a heat module can be added to the model to obtain a more realistic situation. The heat module can be used to simulate the temperature of the trap and the surroundings to evaluate the blackbody radiation frequency shift in the OFS.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] |