When a free electron collides with an ion, the ion may capture the free electron through a non-resonant photon emission process called radiative recombination (RR), or through the resonant processes called dielectronic recombination (DR) where the ion is simultaneously excited. For the DR process, a single electron of the ion is excited and the recombined ion becomes doubly excited, then it stabilizes through radiative decays later. The DR process is commonly considered as an inverse Auger process. DR is the dominant electron–ion recombination process in many plasmas, thus it is of considerable importance for understanding the basic atomic collision phenomena.^[1–3] The dielectronic recombination also plays a crucial role for accurate plasma modeling and spectral analysis in astrophysics depending on its strong impact on the level populations and the ionization balance of plasma.^[4,5] In the DR process, to form a doubly excited intermediate state, the sum of the binding energy of the recombined state and the kinetic energy of the incident electron must match the excitation energy of the inner shell electron of the ion. Thus accurate measurements of DR resonances can be applied to probe the many-body, relativistic, and quantum electrodynamics (QED) effects and can offer critical examinations among state-of-the-art atomic structure theories.^[6,7] On the other hand, it also can be seen from the previous electron–ion recombination experiments that the theoretical calculations still have problems in reconstructing the experimental results for open M-shell ions.^[8,9] Therefore, the experimental measurements for multi-electron ions are of importance for further theoretical improvement.

It should be noted that for the higher order resonant capture of a free electron, two bound electrons can be simultaneously excited, leading to trielectronic recombination (TR).^[10,11] Recent investigations revealed that TR is comparable or even overwhelms the first-order DR process for some ionic species in light elements, and then becomes the dominate ion-electron recombination channel.^[12] However, the trielectronic recombination of the electron–ion collision experiment has been investigated mostly on the Be-like ion, and the clear identification of the TR contribution has not been observed on the complex highly charged ions yet, to the best of our knowledge.

Over recent decades, the field of recombination of highly charged ions with free electrons has reached an unforeseen level. Electron–ion recombination experiments employing the merged-beam technique at heavy-ion storage rings equipped with electron coolers are developed at several places, including TSR at MPIK in Heidelberg,^[13] the ESR at GSI in Darmstadt,^[14] Germany, the CRYRING in Stockholm,^[15] Sweden, and also the main cooler storage ring (CSRm) of the Heavy Ion Research Facility in Lanzhou (HIRFL) at the Institute of Modern Physics (IMP),^[16] China. These experiments are particularly sensitive to the resonance energies and widths in the near zero relative energy region,^[6,17] therefore, have a potential for high-resolution spectroscopy of the multi-excited states.^[18–20] It is important to note that, the electron–ion recombination experiments on highly charged ions have also been performed at electron beam ion traps (EBIT);^[21,22] details of the DR experiments at EBIT can be found in the literature.^[23–25]

Here, we present absolute rate coefficients for electron–ion recombination of P-like tin measured at the main cooler storage ring CSRm and calculated using the FAC code. The relevant channels for DR of the ¹¹²Sn³⁵⁺ ion are:

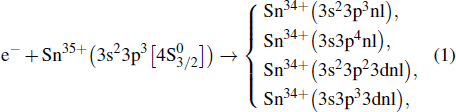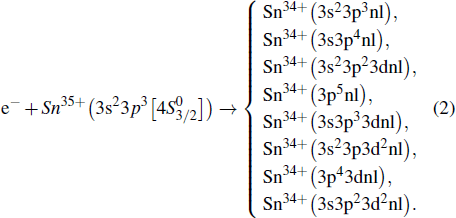Since the ¹¹²Sn³⁵⁺ ion has a complex electron structure and a considerably heavy nucleus, the present experimental result serves a valuable examination to the theoretical calculations of the relativistic many-body perturbation theory (RMBPT) and radiative QED theory. Here, we report the first measurement of the electron–ion recombination spectrum of the ¹¹²Sn³⁵⁺ ion. The paper is structured as follows. The experimental setup and the measuring procedure are described in Section 2. In Section 3, we briefly explain the theoretical calculation using the FAC code. In Section 4, the data analysis is discussed, and then the experimental results are presented and compared with the theoretical calculation. A brief summary is given in Section 5.

This experiment was performed at the CSRm at the Institute of Modern Physics (IMP) in Lanzhou, China. A detailed description of the experimental setup and method for DR experiments at the CSRm has already been given in the literature.^[16,26] Here, we will only briefly describe the electron–ion recombination experiment with P-like ¹¹²Sn³⁵⁺ at the CSRm. The ¹¹²Sn³⁵⁺ ions were produced by an electron cyclotron resonant ion source and accelerated by a sector focused cyclotron to an energy of 3.7 MeV/u. The ion beam was then injected into the CSRm for recombination experiments. The current of ion beam in the storage ring was enhanced by multiturn injection and e-cool stacking, then the typical beam current of 50 μA–60 μA was achieved corresponding to about 6 × 10⁷ ions stored in the ring. The ion beam was cooled in phase space by a 3-kV e-cooler to optimize its quality through merging it with a velocity matched electron beam over an effective interaction length of 4 m, then the relative momentum spread can be reduced to about 2 × 10⁻⁴.^[27] In addition, the electron beam used for cooling the ion beams was also employed as the electron–target for recombination experiments. The recombined ions in the e-cooler changed their charge states and were separated from the initial ion beam by the first dipole magnet downstream from the e-cooler, finally they were detected by the movable scintillator particle detector (YAP:Ce + PMT) with a 100% detection efficiency.^[28]

In the experiment, after each multiturn injection, the ion beam was cooled for about 2 s before data acquisition to ensure the ion beam quality. During the measurement, a time cycle of a 10-ms detuning with the electron beam energy deviating from the E_c followed by a 190-ms electron-cooling to maintain the ion beam quality was applied. The relative energy scan is accomplished by changing the cathode voltage of the electron cooler in the 10-ms detuning period. Considering the lifetime of the ion beam, the time-length of the injection period and the statistical uncertainties of the counts, a measuring time of 35 s for each detuning voltage is chosen along with a voltage step of 1 V.

The counts of recombined ¹¹²Sn³⁴⁺ ions recorded by the detector can be transferred into the total recombination rate coefficient α according to the following formula:

The relative collision energy between electrons and ions in the center-of-mass (c.m.) frame can be written as:

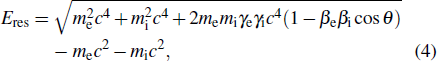The Flexible Atomic Code (FAC)^[31] was employed to calculate the cross-sections of the transitions in the energy region of 0 eV–14 eV for electron–ion recombination of ¹¹²Sn³⁵⁺. The calculations for ΔN = 0 core excitations were carried out in intermediate coupling using a configuration interaction expansion for the ¹¹²Sn³⁵⁺ 15-electron target involving an Ne-like core and valence configurations of 3s²3p³, 3s3p⁴, 3s²3p²3d, 3p⁵, 3s3p³3d, 3s²3p3d², 3p⁴3d, and 3s3p²3d² to which continuum and Rydberg electron orbitals were coupled. Since there are more than 2000 transitions in the energy region of 0 eV–14 eV, the merged-beam experiment cannot resolve the final states and all of the results that we presented are the total recombination cross section, i.e., sum over all final states that stabilize through photon emission against autoionization or field ionization in CSRm before they are detected.

The cross section, as a function of the c.m. energy E, from an initial state i via a doubly excited state d with a small natural width compared with E can be represented in a good approximation by^[32,33]

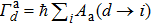
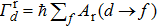
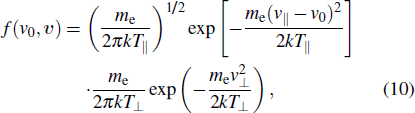The present experimental rate coefficients are plotted in Fig. 1 along with the theoretical rate coefficients obtained from the calculated resonance strengths convoluted with the electron beam velocity distribution. The electron beam temperatures were determined as K_BT_⊥ = 40 meV and K_BT_|| = 0.8 meV in the previous experiment.^[16] The DR transitions of the ground state 3s² 3p³[²D_3/2, ²D_5/2, ²P_1/2, ²P_3/2] are also labeled in Fig. 1 (²P_3/2 series are out of the present energy region) based on the Rydberg formula:

Fig. 1.

Figure Option ViewDownloadNew Window

Fig. 1. (color online) Comparison of the presently measured absolute recombination rate coefficients of 112Sn35+ ions in 0 eV–14 eV with the calculation by an FAC code. The blue dots are the experimental results (the RR rate and constant background have been subtracted). The shaded area represents the calculated total recombination rate coefficients for DR and TR. The red solid line is the contributions of DR channels while the purple solid line is the TR part of the calculated result. The calculated rate coefficients are shifted for about 0.77 eV towards lower energy region for comparison.

Considering the high accumulated count of each point, the statistical error remains below 1% for the raw spectrum. The uncertainty of the ion beam current, monitored by a DC beam-current transformer, is about 3%–5% according to its unclarified background. The uncertainty of the electron beam current is about 1% and the one from the corrections for the merging and demerging of the beams is also about 1%. It should be noted that, uncertainties introduced by some factors such as the vacuum are hard to be quantified, thus the measurement of the reference rate coefficients α₀ is applied during the experiment to estimate the influences of these factors. α₀ here is the total recombination rate coefficients at zero relative energy, which is actually dominated by the RR rate coefficients. Due to that the RR rate coefficients decrease dramatically when the collision energy deviates from zero, α₀ is very sensitive to the variation of the experiment conditions. During the experiment, α₀ was measured at the cooling phases just before the detuning start for each voltage point. According to the variation of α₀ measured though the experiment period, a 5% error is taken into account, and the overall accuracy of the electron recombination rate coefficient is given as 8% safely without considering the contributions of subtracting the RR rate coefficient and background. When they are taken into account, an error of about 15% more should be added.

The uncertainty of the energy scale in the electron–ion c.m. frame is a bit more complex. During the experiment, we varied the electron energy to find the cooling energy E_c where the velocity of electrons matches that of the ions. Thus the cooling condition is determined experimentally and the difference between the preset value of the ion energy and the real ion energy do not contribute to the collision energy uncertainty. One source of the uncertainty is due to the discrepancy of the actual cathode voltage to the preset voltage value. According to the claimed precision of the power supply, this contribution is estimated as 0.8% over the entire c.m. energy range. The space-charge potential correction also offered a relative correction of about 5% to the final relative energy, so it may introduce the uncertainty. A beam alignment of θ = 0 ± 0.8 mrad is routinely achieved, which introduced a 0.15% influence to the collision energy. All factors discussed so far give a 1% relative uncertainty to the relative energy, and there still remains an error of 15 meV according to the calibration of the zero c.m. energy point.

It should be noted that the ¹¹²Sn³⁵⁺ resonance spectrum is very rich and there are many satellite lines involved in the spectrum for each n. Therefore, the individual assignments of the recombination spectrum are essentially impossible for this open M-shell ion. Nevertheless, we can still identify that the 3s 3p⁴ and 3s² 3p² 3d series are the strongest ones, and the 3s 3p³ 3d series is influential in some region. Comparing the experimental rate coefficients with the shifted theoretical results, a reasonable agreement was found between them. The calculation misses some peaks in the region lower than 0.5 eV in Fig. 1 resulting from the energy shift for the calculated spectrum. Furthermore, the calculated one in this region is about 3 times of the experimental one, which can be due to the well-known difficulty of calculating DR resonance positions at low energies. In 0.5 eV–2 eV, the theory gives two peaks which is similar with the experimental observation but with lower strength. In the energy range of 2 eV–5 eV both experiment and theory have three peaks while their positions and strengths are different. In the energy range of 5 eV–7.5 eV, the experiment shows one big peak while the theory give three. It seems that the theory misses some transitions or underestimates the strengths of some transitions. In the range of 9 eV–10.5 eV, theory reproduces the experimental observation well. The theoretical calculations in 11 eV–13 eV are a bit lower than the experimental ones. The aforementioned differences between the experimental and the theoretical rate coefficients are mainly caused by the limited accuracy of the theoretical calculation, especially for the open-M ions like ¹¹²Sn³⁵⁺ and Fe¹¹⁺.^[9] The contributions of the DR and the TR processes are recognized from the calculated results. It can be seen from Fig. 1, the DR process still dominates in the whole energy region while TR channels play important roles in some regions, which indicates that the TR process can also be the important path of ion–electron recombination for multi-electron highly charged ions.

The electron–ion recombination rate coefficients of Phosphorus-like ¹¹²Sn³⁵⁺ over the collision energy range of 0 eV–14 eV were measured at the heavy ion storage ring CSRm with an electron–ion merged-beams technique. Theoretical calculations using the Flexible Atomic Code were performed to compare with the experimental results. From the calculated electron–ion recombination rate coefficients, the TR contribution has been identified for the first time of the complex highly charged ions, to the best of our knowledge. It is found that TR has a substantial contribution to the measured electron–ion recombination spectrum, while DR is still the dominate process. A reasonable agreement between the experimental and theoretical results is found over the entire electron–ion collision energy region. The discrepancies can be mainly attributed to the limited accuracy of the theoretical calculation, therefore, further efforts are greatly recommended both experimentally and theoretically to investigate the precise spectroscopy of electron–ion recombination for open M-shell ions.