Project supported by the National Natural Science Foundation of China (Grant Nos. 51574016 and 51604018).
Project supported by the National Natural Science Foundation of China (Grant Nos. 51574016 and 51604018).
† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 51574016 and 51604018).
The dynamics of the ground-state reaction of CH4 + O(3P) → CH3(ν = 0) + OH(ν′ = 0) have attracted a great deal of attention both theoretically and experimentally. This rapid communication represents extensive quasi-classical trajectory calculations of the vibrational distributions on a unique full-dimensional ab initio potential energy surface for the title reaction, at the collision energy of relevance to previous crossed molecular beam experiments. The surface is constructed using the all electrons coupled-cluster singles and doubles approach plus quasi-perturbative triple excitations with optimized basis sets. A modified Shepard interpolation method is also employed for the construction. Good agreement between our calculations and the available experimental results has been achieved, opening the door for accurate dynamics on this surface.
Methane is the simplest organic fuel and the most abundant hydrocarbon in the atmosphere.[1–10] Representing an important initial step in methane combustion, the CH4 + O(3P) → CH3(ν = 0) + OH(ν′ = 0) reaction provides an ideal platform for studying bimolecular reactions involving one transfer of a hydrogen atom.[11–15] Over the last decade, experimental and theoretical studies on this reaction have greatly extended and advanced our understanding of chemical reaction dynamics.[16–21] Suzuki and co-workers measured the nascent ν2 out-of-plane bending vibrational distribution in the umbrella mode of CH3 by an infrared diode laser absorption kinetic spectroscopy experiment, which suggested that the CH3 moiety was gradually relaxed to a planar structure during these reactions.[22] Later Sweeney et al. measured the very low fractions of product rotational energy release for the higher homologues such as isobutane and cyclohexane by laser photolysis of NO2 combined with laser-induced fluorescence detection of the nascent OH product.[16] The OH spin–orbit states were found to be nonstatistically populated, which was interpreted by a direct abstraction mechanism with a preferentially collinear C–H–O approach of the O(3P) atom to the C–H bond under attack. Moreover, a considerable body of work[23–26] was devoted to the experimental characterization of the OH molecule produced in related processes via molecular beams, like the reactions of the O(3P) atom with saturated, unsaturated aromatic hydrocarbons. Many correlated experiments on methane with H, F, Cl, and O(3P) have been reported after the first measurement of correlated angular and vibrational product distributions for the F + CD4.[27]
Recently, there has been additional progress with a wide variety of methods, including the crossed beam technique, on the title reaction.[20,21,25,26,28] The internal energy distributions of products CH3 and OH, as well as differential cross sections, were studied with isotopic variants taken into account to provide detailed information on product translational, vibrational energy distributions, and product angular distributions. The product speed distributions at different Ecol were measured by a number of groups and the excitation functions were also obtained.[20,21] The reactions at center-of-mass collision energies in the range of 64.6 kcal/mol–89.9 kcal/mol were investigated with crossed-beams experiments and direct dynamics calculations, which provided evidence for the expected H–atom abstraction reaction.[20] This reaction was also studied at a hyperthermal collision energy of 64 kcal/mol by two crossed-molecular-beams techniques, in which the OH product was formed mainly from a stripping mechanism where the O(3P) reacts through large-impact-parameter collisions with CH4. The CH3 products are in the ground vibrational state, while the OH products are vibrationally cold and rotationally hot.[21] With extended collision energies ranging from 7.5 kcal/mol to 13.5 kcal/mol, it was revealed that the product angular distributions were backward scattered for the O(3P) + CHD3 reaction, which indicated a direct rebound mechanism. Liu and his co-worker measured the first differential cross sections, in which the first reported product angular distributions showed predominant backward scatterings for both ground-state and bend-excited methanes, indicating a direct rebound reaction mechanism.[29] Later, they measured the reactive excitation function, as well as the product angular distributions and the energy disposal on initial collision energies, by taking images over the energy range of chemical significance.[21,25,26,28] These experimental results are a severe test for theoretical work on potential energy surface (PES) constructions and quasiclassical trajectory (QCT) calculations. The intersection angle of the two molecular beams was varied to investigate the initial translational energy dependence of the reactivity, thereby changing the relative collision energy in the center-of-mass frame. The ground state reaction producing OH + CD3 has a threshold at 8.01 kcal/mol. Significant vibrational enhancement in the reaction rate was observed, and the product angular distribution shifted from a backward-dominance in O(3P) + CHD3 to a sideways-peaking upon CH stretching excitation.[25] Moreover,due to the focusing effects of the long-range anisotropic interactions en route to the barrier, vibrationally enhanced reactivity has also been observed in CHD3 (ν1 = 1) by enlarging the cone of the reactive acceptance. Later, by imaging the effects of the antisymmetric-stretching excitation, it was found that the OH(ν′ = 0) product was associated with a single peak, while the stretch-excited methane presented two peaks corresponding to the OH(ν′ = 1) and OH(ν′ = 1) states with populations 0.85:0.15 at Ecol = 12.4 kcal/mol.[30] A reactive threshold at Ecol ≈ 8 kcal/mol was clearly discerned, which predicted the barrier height of 9 kcal/mol–10 kcal/mol. These quantitative results for the ground-state reaction provide a stringent test for further theoretical developments of the potential energy surface and dynamics calculations of this important polyatomic reaction.[25,30–32]
Theoretically, it has received a great deal of attention using various ab initio and dynamical methods.[33–37] Early in 1980, Walch and Dunning[33] studied the stationary points on the ground state PES with POL-CI wave functions. In 1990, Gonzalez et al. performed the geometry optimization of all stationary points including transition states in this reaction with the Hartree–Fock method.[34] The accurate dynamic investigation of the title reaction usually needs an accurate PES.[11,12,36,38–44] Until now, there have been several PESs constructed for the O(3P) + CH4 → OH + CH3 reaction, some QCT and reduced-dimensional quantum dynamics (QD) calculations have been performed using these PESs. The ground PES, constructed by Gonzáleza and co-authors[35] using the PMP4 calculations, were employed to obtain the barrier height of 13.3 kcal/mol and the zero-point-inclusive barrier height of 9.4 kcal/mol. Based on the information furnished by Joseph et al.[45] and Jordan et al.[46] for the CH4(X1A1) + H → CH3 + H2 reaction, a 12-dimensional analytical PES was constructed[12,38] by making the previous one completely symmetric with respect to any permutation of the four methane hydrogens. In 2012, the high accuracy was achieved by using a large basis set and high-level electron correlation method to obtain the barrier height of 14.08 kcal/mol and the OHC bending angle of 179.3° at the saddle point, which was taken as a benchmark value.[40] In a recent study, a new full-dimensional analytical PES for O(3P) + CH4 was accurately constructed based on PES-2000 and further high level CCSD(T) = FULL/aug-cc-pVQZ ab initio data by González-Lavado and co-authors.[41] They concluded that the correlation of all electrons (FULL), including core and valence electrons, has a major influence on the description of the barrier. The barrier height obtained from this surface was 14.0 kcal/mol with the corresponding OHC bending angle of 180.0°. The title reaction, theoretically, has also received a great deal of attention using QCT calculations.[35,47,48] The mode-specific vibrational distributions were obtained by doing a normal-mode analysis, and the reaction was predicted to occur at small impact parameters and proceed through direct rebound pathways.[48] That the translational energy activates the reaction more efficiently than vibrational energy shows this central-barrier reaction behaves more like an early barrier reaction.
In the present study, we investigate the QCT calculations on the uniquely developed ground-state PES for the gas-phase O(3P) + CH4 → OH + CH3 reaction with the 3A″ transition state. The dynamical details of the title reaction are compared with the results of the universal crossed molecular beam experiments performed by Liu and his co-workers.[13,25,26,28,30]
The ground PES for the gas-phase reaction of hydrogen-abstraction from methane by an oxygen atom has been performed using the all electrons coupled-cluster singles and doubles approach plus quasi-perturbative triples excitations. The ab initio calculations in the present work are conducted using the Gaussian 09 suite of ab initio programs.[49] The best compromise we could achieve was the all-electron coupled-cluster singles and doubles approach plus quasi-perturbative triples excitations, CCSD(T) (full), together with optimized aug-cc-pCVQZ basis sets. A reasonable consideration of the basis sets dependence is included. Several basis sets, including cc-pVXZ [X = D, T, Q, and 5], aug-cc-pCVXZ [X = D, T, and Q] and an optimized aug-cc-pCVQZ have been tested to obtain the reasonable barrier height and reaction endoergicity. Some results with previous reported calculations are presented schematically in Fig.
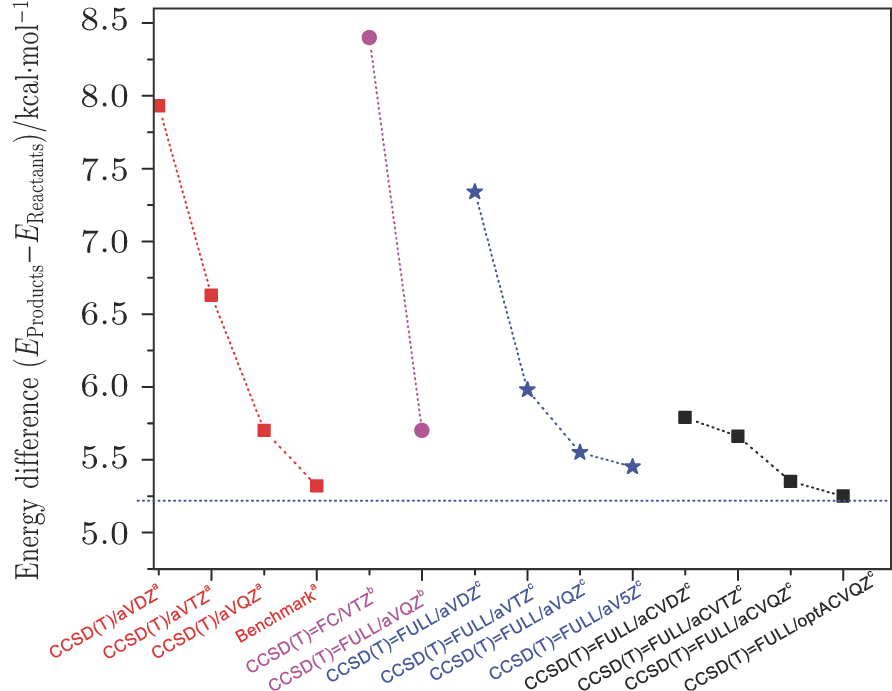 | Fig. 1. (color online) The comparison of reaction endoergicity with various ab initio methods. a: CCSD(T)/aug-cc-pCVQZ calculations from Ref. [40]; b: the valence-electron CCSD(T)/(FC)cc-pVTZ level and the all-electron CCSD(T)/(FULL)aug-cc-pVQZ level from Ref. [41]; c: present work at the CCSD(T)=FULL/optACVQZ level. The energy of the O(3P) + CH4(X1A1) asymptote is taken to be zero. |
A modified Shepard interpolation method is employed for the construction of PES. This method was proposed by Collins and his co-workers[54–57] for systematically generating global ab initio PES for systems of more than four atoms. The PES is determined by the energies and the first and second order derivatives of the energy at a set of data point geometries.[54,55,58,59] Our interpolated PES in the present work for the reaction O(3P) + CH4 → OH + CH3 is grown from the initial set of 196 data points, and finally about 6100 data points are obtained. QCT calculations of the title reaction on the ground rovibrational state are performed using this new ab initio PES. The ability to perform classical dynamics simulations on multidimensional PES is limited in practice due to the exponential scaling with the number of nuclear degrees of freedom. The location of the data points is mainly determined using the iterative methods developed by Collins and his co-workers and the iterative development of the PES is implemented with the GROW package.[54,60,61] A set of geometries are chosen as an initial set of data points for GROW. These points should represent the chemically important regions in configuration space, typically the reactants, products, a saddle point, van der Waals potential wells and some configurations on a minimum energy path for the reaction. Additionally, some data points should be added according to physical considerations, particulary the analysis of potential contour plots.
This new global 12-dimensional potential energy surface (denoted as PES-2017) using the methods described in the above for the gas-phase O(3P) + CH4 → OH + CH3 reaction is expected to give a better description of the regions around the transition state (TS), and of those long-range vdW interactions (reactant complex WellR, 
The transition state geometric parameters from our ab initio calculations and previous works in the literature are shown in Fig.
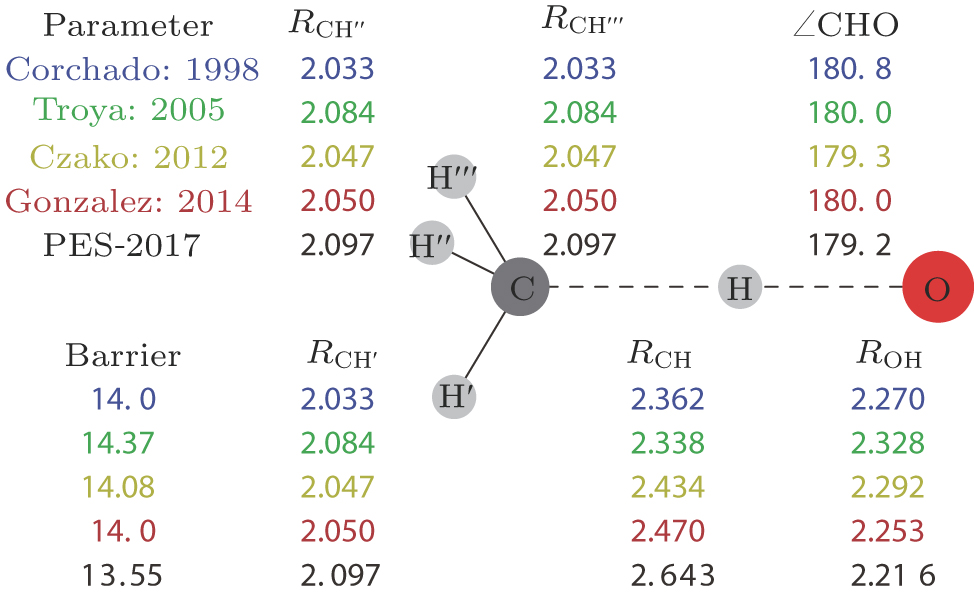 | Fig. 2. (color online) Structural parameters (distances in bohr, angles in degrees and energies in units kcal/mol) for the transition state obtained from various ab initio levels. Corchado: geometry at the UMP2/cc-pVTZ level and energy at the PUMP2-SAC//UMP2/cc-pVTZ level from Ref. [38]; Troya: PMP2/aug-cc-pVDZ from Ref. [19]; Czako: all-electron CCSD(T)/aug-cc-pCVQZ from Ref. [40]; Gonzalez: geometry at the valence-electron CCSD(T)/cc-pVTZ level and energy at the all-electron CCSD(T)/cc-pVQZ level from Ref. [41]; PES-2017: our present work. |
In our study, the geometry parameters of WellR includes θ = 0.0°, ROH = 6.012 bohr, RCH = 2.103 bohr. The depth of WellR on PES-2017 is −0.53 kcal/mol, which is much deeper than previous reported values. Therefore, our result indicates that the weakly-bound vdW interaction of the ground-state O atom with methane along the O⋯HCH3 axis is helpful for orienting the system toward WellR. The overall accuracy of the interpolation for the PES-2017 surface is estimated roughly as follows. Two thousand molecular configurations were randomly selected during the integration of trajectories to produce a sample of dynamically relevant geometries. Then ab initio calculations at the CCSD(T) = FULL/optACVQZ level are performed at all configurations in this sample, and the error is computed from the difference between the ab initio energy and the value obtained from the interpolated surface. The average absolute error is obtained to be 0.60 kcal/mol, and the root-mean-square error is 0.83 kcal/mol.
The full-dimensional QCT calculations with the standard normal-mode sampling for the title reaction are carried out on the newly constructed PES with CH4 initially in the ground rovibrational state. Two thousand molecular configurations are randomly selected during the integration of trajectories to produce a sample of dynamically relevant geometries. In this step, the initial distance between the center of mass of the reactants is (x2 + b2)1/2, where b is the impact parameter and x = 10 bohr. Then ab initio calculations at the CCSD(T) = FULL/optACVQZ level are performed at all configurations in this sample, and the error is computed from the difference between the ab initio energy and the value obtained from the interpolated surface. The average absolute error is obtained to be 0.60 kcal/mol, and the root-mean-square error is 0.83 kcal/mol. The initial CH4 molecule is set in its ground rovibrational state using fixed normal mode energy sampling for all trajectories, and the integration time step is 0.05 fs. The initio rotational angular momentum of the fragments and the impact parameter are set to zero. The maximum value of the impact parameter is estimated by calculating batches of 103 trajectories at fixed values of b and systematically increasing the value of the bmax until no reactive trajectories are obtained. It should be noted that the QCT calculations are started at the Reactants asymptote with a center of mass separation between the fragments of 30.0 bohr and are stopped when the O–C or one of the C–H internuclear distance reaches 30.0 bohr after the inner turning point of the trajectories.
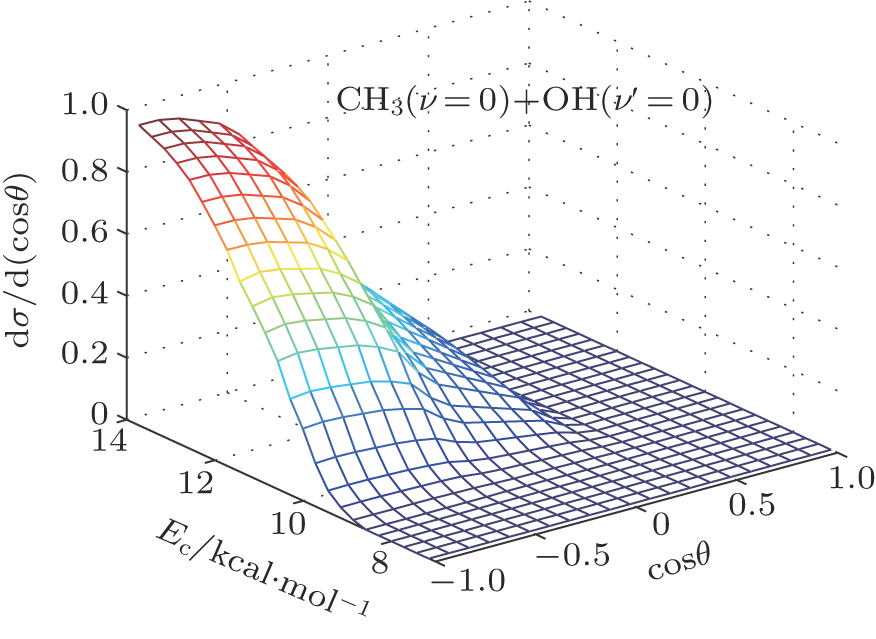
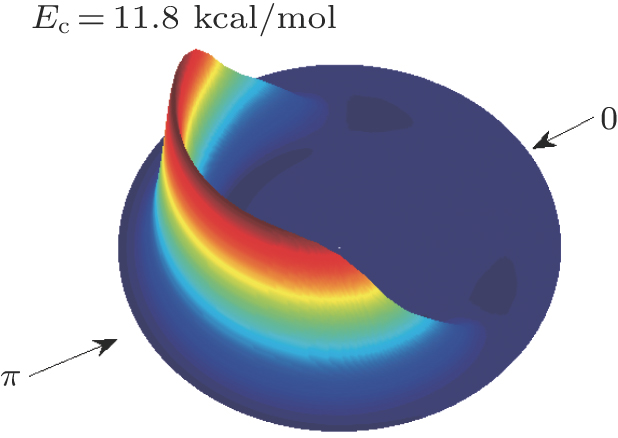
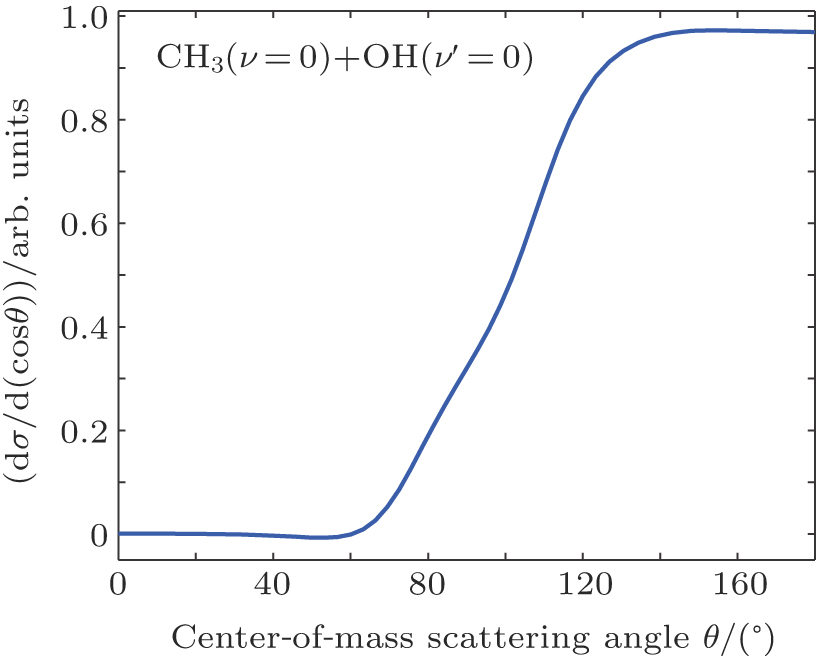
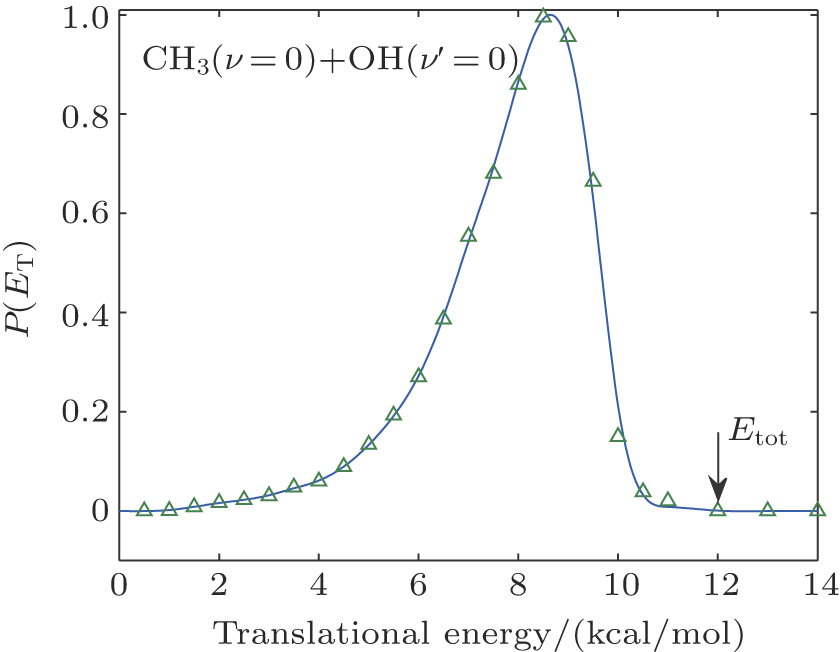
In the calculations for the reaction probability, the reaction probability from the dynamics calculation was multiplied by a factor of 4 to account for equal and independent contribution to reaction probability from all the hydrogen atoms in CH4, due to the fact that the hydrogen atom in the reagent CH4 is treated as distinguishable. Clearly, the reaction probability computed with the classical dynamics is converged to 0.12 with small variations after the reference data set grew to 4500 points. For each energy the maximum value of the impact parameter, bmax, was determined by first calculating batches of 104 trajectories at fixed values of the impact parameter and then systematically increasing the value of b until no reactive trajectories were obtained. For the title reaction at Ecol = 30.0 kcal/mol at 300 K, about 5.6 × 105 trajectories have been calculated, which leads to a maximum impact parameter of 5.0 bohr and an average reaction probability of 0.13. An analogous number of trajectories have also been calculated at 100 K, leading to very similar results. The computed angular distributions for the pair-correlated CH3(ν = 0) + OH(ν′ = 0) products and the center of mass speed distribution P(ET) obtained by the QCT calculations with Ecol = 13.0 kcal/mol on the newly constructed PES are displayed in Fig.
 | Fig. 3. (color online) Translation energy distribution of products obtained from the QCT calculation. |
 | Fig. 4. (color online) Angular distribution of OH(ν′ = 0) relative to the direction of the incoming O atom. The forward direction, 0°, is along the initial CH3 direction in the center-of-mass frame. |
In this paper, we presented extensive QCT calculations for the ground-state reaction of CH4 + O(3P) → CH3(ν = 0) + OH(ν′ = 0) with the detailed dynamics information performed on a unique full-dimensional ab initio PES. The accuracy was achieved by using high-level ab initio calculations to compute about 6100 data points with energies and the first and second order derivatives. The modified Shepard interpolation method and the iterative development scheme are employed to construct the interpolated PES. The analysis of properties of our surface shows that it is accurate in important regions and physically reasonable in various regions. QCT computations on this new PES provide a result in good agreement with the experiments and our previous calculations. The rebound mechanism for the title reaction is confirmed by our QCT calculations.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] | |
| [64] |