Project supported by the National Key Research and Development Program of China (Grant No. 2017YFA0402300), the National Natural Science Foundation of China (Grant Nos. 11774344 and 11474033), and the Joint Foundation of the National Natural Science Foundation and the China Academy of Engineering Physics (Grant No. U1330117).
Project supported by the National Key Research and Development Program of China (Grant No. 2017YFA0402300), the National Natural Science Foundation of China (Grant Nos. 11774344 and 11474033), and the Joint Foundation of the National Natural Science Foundation and the China Academy of Engineering Physics (Grant No. U1330117).
† Corresponding author. E-mail:
Project supported by the National Key Research and Development Program of China (Grant No. 2017YFA0402300), the National Natural Science Foundation of China (Grant Nos. 11774344 and 11474033), and the Joint Foundation of the National Natural Science Foundation and the China Academy of Engineering Physics (Grant No. U1330117).
Single (SA) and double (DA) Auger decay including cascade and direct processes are investigated for Hg 4f−1 with multiconfiguration Dirac–Fock method and two-step approaches, i.e., knockout and shakeoff mechanisms. Due to the computational effort, only the major transitions are considered to describe the SA and DA decays for the Hg+ ions with complex electronic configurations. In order to estimate the Auger transition energies and amplitudes, the reference configuration sets producing the configuration state functions are carefully chosen for balancing electron correlations among the successive singly, doubly and triply ionized mercury. The Auger rates and electron spectra, DA probabilities as well as the populations of the final Hg3+ states are obtained. Our results well explain the recent experimental data about the 4f hole states of Hg [Palaudoux J et al., Phys. Rev. A 
A hole state of atom is created when a core electron is ionized to continuum orbit by photon, electron, or ion impact. This vacancy could be filled by one outer-shell electron during which it emits an Auger electron, i.e., single Auger (SA) decay, or two Auger electrons, i.e., double Auger (DA) decay. The Auger decay is a nonradiative process that results from Coulomb interaction between electrons. Therefore, the Auger spectroscopy is a powerful tool for investigating electron correlation effects and many-body problems in atomic processes.[1–3] Besides, the Auger spectrum also offers valuable information about the electronic structures of atoms and molecules as the transition energy of the Auger decay depends only on initial core-hole state and final state.[4]
Carlson and Krause[5] first reported the experimental evidence of DA decay by detecting the yields of Ne3+ formed by Ne 1s−1 decay, which has been studied extensively by experimental and theoretical studies over the past several decades[2,3,6–20] since it is essentially responsible for the total Auger intensity. The DA decay could occur by a cascade process where two electrons are emitted stepwise through the creation and decay of an intermediate autoionizing state.[8,9] Apart from the cascade DA, the significant contributions of a direct DA that emits two electrons simultaneously sharing the transition energy, have been demonstrated by experimental studies.[2,12–15] For example, Viefhaus et al.[2] demonstrated the existence of the direct process and revealed that it is dominant for the DA decay of Ar 2p−1, by angle-resolved electron–electron coincidence spectroscopy. Hikosaka et al.[12] reported the experimental spectra displaying the Ar2+ states populated via direct DA decay following the resonantly excited 2p in Ar. The relative direct and cascade DA probabilities of Ne 1s−1 are found to be 3.2% and 2.8%, respectively, which indicates that the contributions of the direct and cascade processes are comparable.[14] Recently, even the direct triple Auger decay was observed,[16] and were investigated theoretically in our previous work[17] by using the shakeoff (SO) and knockout (KO) mechanisms.[21] Therefore, in many cases both the cascade and direct processes should be considered for the DA decays.
Mercury is a heavy element with complex electronic configuration (ground configuration [Kr]4d105s24f145p65d106s2 and [Kr] represents the ground configuration with 36 electrons in neutral Kr), the core–hole states studied experimentally by using a multielectron coincidence detection technique, have received much attention.[18,22–26] For example, Andersson et al.[22] reported the experimental SA and DA spectra for the metal Hg with a 4d hole and analyzed the cascade DA decays by the multiconfiguration Dirac–Fock (MCDF) method. Palaudoux et al.[18] obtained the DA probabilities and the populations of Hg3+ states produced by DA decays of the 4f−1 and 5p−1 hole. They also made the calculations to explain the experimental results, but could not produce the reasonable DA probabilities and population of final Hg3+ states. A possible reason for this might be that the direct processes were not taken into account in their calculations.
In this work, the theoretical investigations are presented for elucidating the SA and DA decays following the 4f inner-shell ionization of Hg. The direct processes are considered for the DA decay by using two-step approaches, i.e., KO and SO within the framework of the perturbation theory.[21] Besides, the MCDF method[27] is utilized to evaluate the SA transition energy and amplitude. In the practical calculations, the reference configuration sets producing the configuration state functions (CSFs) are chosen for balancing electron correlations since three different successive near-neutral Hg ions, i.e., Hg+, Hg2+, and Hg3+ are involved. Finally, our results show good agreement with experimental results[18] about the DA probabilities and populations of final Hg3+ states.
The bound-state wave functions with parity P and total angular momentum J for the various Hg ions involved in the Auger decay, are constructed by a CI-type function that is approximated by a linear expansion of CSFs with the same symmetry,
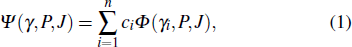 |
The SA decay rate can be obtained from[29]
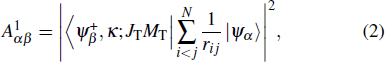 |
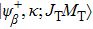

In the cascade process, initial autoionizing state primarily decays to intermediate state that is embed energetically in continuum of the next-higher-charge state of ion and will decay further. The cascade DA rate can be obtained from the following expression:
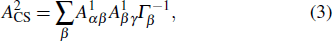 |
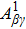
Direct DA is one of the relaxation processes of atoms with an inner-shell vacancy, during which two of outer-shell electrons are emitted simultaneously when a vacancy is filled by another outer-shell electron. This needs a three-body interaction operator for a transition that three single-electron orbitals are changed between the initial and final states. Therefore, we employ the two-step approximate formulas of KO and SO derived from many-body perturbation theory to calculate the direct DA rates.[21]
As shown in our previous work,[17,31] the KO is combined by a primary SA and an inelastic scattering process, in which the second Auger electron may be knocked out of the intermediate ions, i.e., Hg2+ through inelastic scattering by the primary Auger electron with specific energy and angular momentum. The direct DA rate of the KO mechanism can be given by
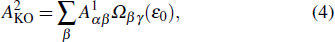 |
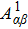
The SO mechanism resulting from that the second Auger electron is ejected following a sudden change of atomic potential caused by a rapid ejection of the primary Auger electron. The direct DA rate of the SO mechanism can be expressed by
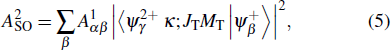 |
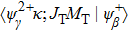
The collision ionization strengths and the overlap integrals between the intermediate and final states are calculated using the flexible atomic code[32] with some modifications,[17] based on Dirac–Fock–Slater approach.
Auger decays strictly caused by electron–electron interaction hence the electron correlation plays a crucial role in accurately estimating the rates.[31,33,34] Generally, increasing the configuration space of Eq. (
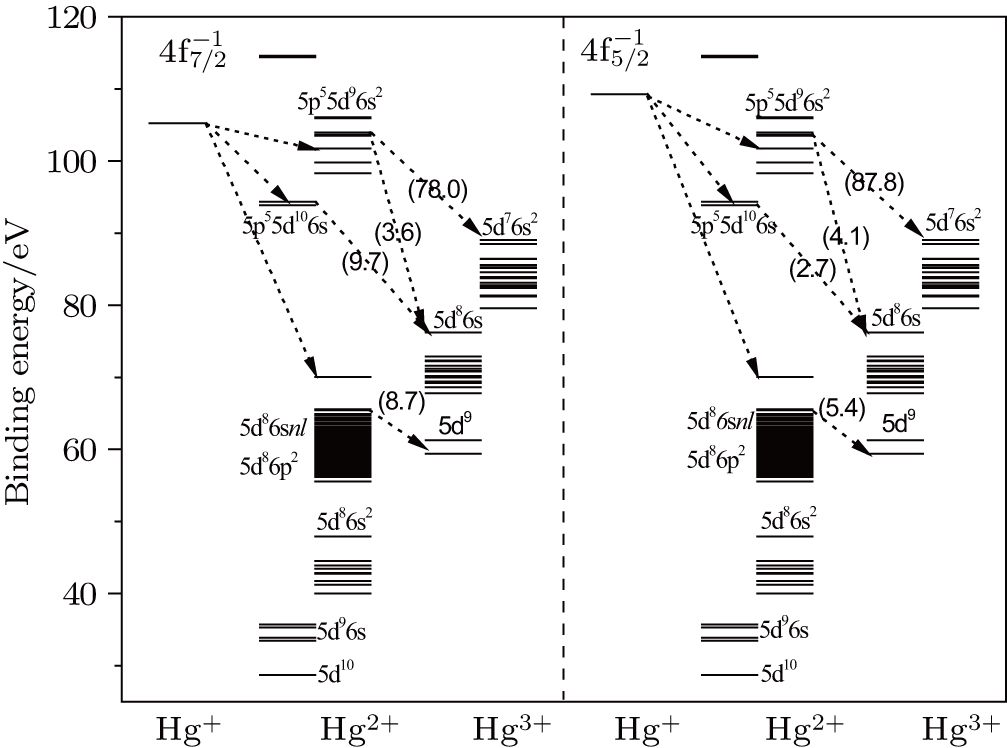
As will be discussed in following sections, the highly excited states,such as 5p55d106s and 5p55d96s2 of Hg2+ could be populated in SA decay of 4f−1 states and will be autoionized further into the Hg3+ states, which results in the cascade DA decay. The energy levels of Hg 4f−1 are located among the levels of the 5p55d106s and 5p55d96s2 in Hg2+, and hence the energy level positions should be determined accurately to figure out the energetically allowed channels for the transitions 4f−1 → 5p55d106s and 5p55d96s2. Furthermore, the inaccuracy of such small transition energies may reduce the reliability of the calculated Auger rates. One could accurately calculate the energies of states by MCDF method, in which the electron correlation is composed of all CSFs that interact with ASFs. Therefore, generating the CSFs is pivotal for capturing the electron correlation effect efficiently, which are obtained by single and double (SD) substitutions from the reference configuration set to virtual orbitals by using the active space (AS) approach.[35] Furthermore, the appropriate reference configuration set are needed to generate the CSF space for the ions with different ionization degrees on the same footing as the balanced correlation considerations are crucially important. For example, in order to determine the transition energies 4f−1 → 5p55d106s and 5p55d96s2, we first only consider the lowest levels of the 4f−1 of Hg+ and 5p55d106s of Hg2+ and treat corresponding configuration as the reference configuration set. The active orbitals are then optimized by variationally determining the eigenenergy of the reference level (namely, the lowest level) for both ions, which is accomplished separately to take into account the relaxation effect. Finally, the splits of the 4f−1 as well as 5p55d106s and 5p55d96s2 are obtained by these configurations serving as the reference configuration set. Then the sets of active orbitals are enlarged to generate the CSFs for the MCDF calculations as follows.
The occupied orbitals are optimized as spectroscopic ones in the reference configuration set mentioned above. The 5d and 6s orbitals are treated as valence, and the others are regarded as core orbitals, which are kept frozen in subsequent calculations. The virtual orbitals are optimized layer by layer up to 9s, 8p, 7d, and 7f orbitals and the CSFs are obtained by SD substitutions from valence orbitals to the virtual ones. This step accommodates the contributions from only valence correlations, which is referred to as the valence–valence (VV) correlation (for the details of the layer-by-layer calculation and generation of the virtual orbitals, please refer to our previous work.[35] The ASFs and the mixing coefficients of Eq. (
As has been illustrated by Cowan,[36] the difference in energy between two successive ions is normally obtained within a satisfying accuracy, the further correlation corrections from the valence g orbitals and core are not included due to the computational capacity, which rapidly increases the number of the CSFs.
The influence of the electron correlation effect on the intensity of the cascade DA decay is significant as demonstrated in our previous study for the Ne 1s−1.[31] The CI approximations including the electron correlation effect are needed to evaluate the Auger transition amplitudes. However, only the main configurations should be included since the numbers of CSFs and transitions increase rapidly and go beyond the computational capability for such a complex case of Hg ions. According to CI scheme, the interactions of the double excitation of 4f135p65d106s2 ↔ 4f135p65d10n′l′nl (with odd parity) and 5p65d86s2 ↔ 5p65d8n′l′nl (with even parity) are most crucial for Hg+ and Hg2+ sates, respectively. Therefore, doubly excited states such as 5p65d8n′l′nl (with even parity) of Hg2+ could be populated (i.e., shakeup processes[37]), some of which lie above the ionization threshold of Hg3+ and may autoionize further into Hg3+ states. As this importance has been illustrated in the Auger cascades of the hole state in Cd atom,[38,39] the shakeup processes are included in this work. Due to the admixture of 6p2 and 6s2, the states 5p6(5d6s)96p (with odd parity) may also be populated in the SA decay where one 6p electron is emitted, i.e., 6s→6p conjugate shakeup process, which were found to be rather weak to include according to the test calculations, just like the case of the resonantly excited neon.[30]
According to the discussion above, the following configurations are considered for describing the main SA and DA decays, which are 4f135p65d106s2 in Hg+ ions, and 5p65d10, 5p65d96s, 5p65d86s2, 5p65d86p2, and 5p65d86snl (nl = 7s, 6d) with even parity, 5p55d106s and 5p55d96s2 in Hg2+ ions, and 5p65d9, 5p65d86s, and 5p65d76s2 in Hg3+ ions. A balanced treatment of the electron correlation is also necessary for obtaining the resulting DA rates. According to the parity of the state in each ion, the above-mentioned configurations with the lowest average energy are treated as the reference configuration sets that are 4f135p65d106s2 for the Hg+ ion, 5p55d106s and 5p65d10 for the Hg2+ ion, and 5p65d9 for the Hg3+ ion. Besides, the CSFs with J > 4 are not included due to the negligible contributions. Based on these reference configuration sets, the sets of active orbitals are optimized up to 7s, 6p, 6d orbitals by steps (i)–(iii) described in Subsection
The primary SA rates for the main configurations are listed in Table 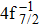
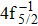
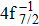

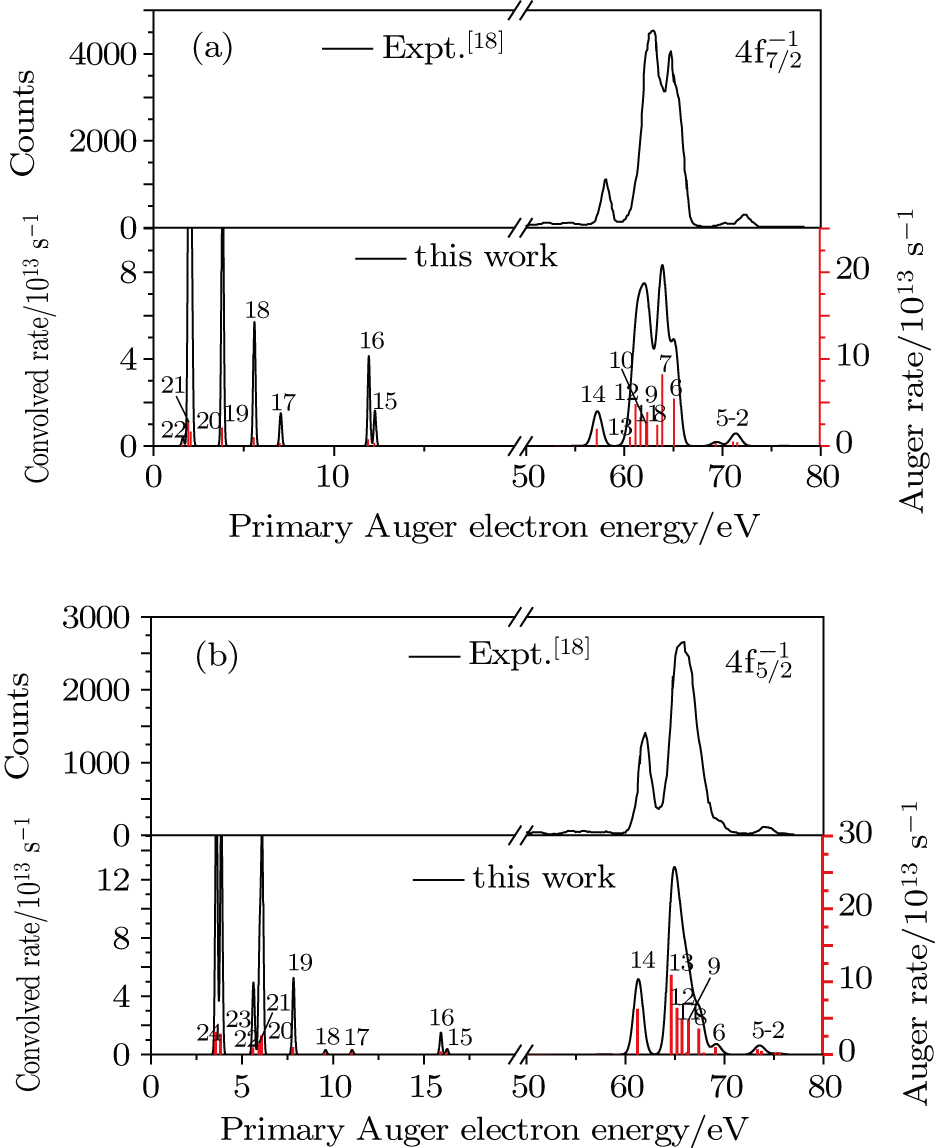 | Fig. 1. (color online) Auger electron spectra for single Auger decay of ionized (a) 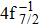 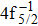 |
| Table 1. Values of Auger electron energy E and rate A1 of main channel for the single Auger of Hg 4f−1 states. . |
In the energy range of 0 eV–20 eV (shown in Fig. 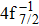
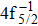
Table 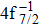
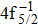
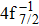
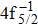
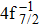

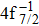
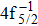
| Table 2. Values of double Auger rate A2 and DA probability P (in percentage) including the cascade and direct processes to the main configurations of Hg3+. . |
In addition to the cascade processes discussed above, it follows from Table 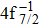
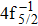

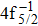
The calculated population of the final states can be directly derived from the Auger rates. To illustrate the contributions from the cascade DA and direct DA processes to the populations of Hg3+ states, the DA rates are convolved with Gaussian profile of 0.7-eV FWHM according to the experimental resolution[18] as shown in Fig. 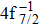
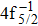

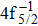
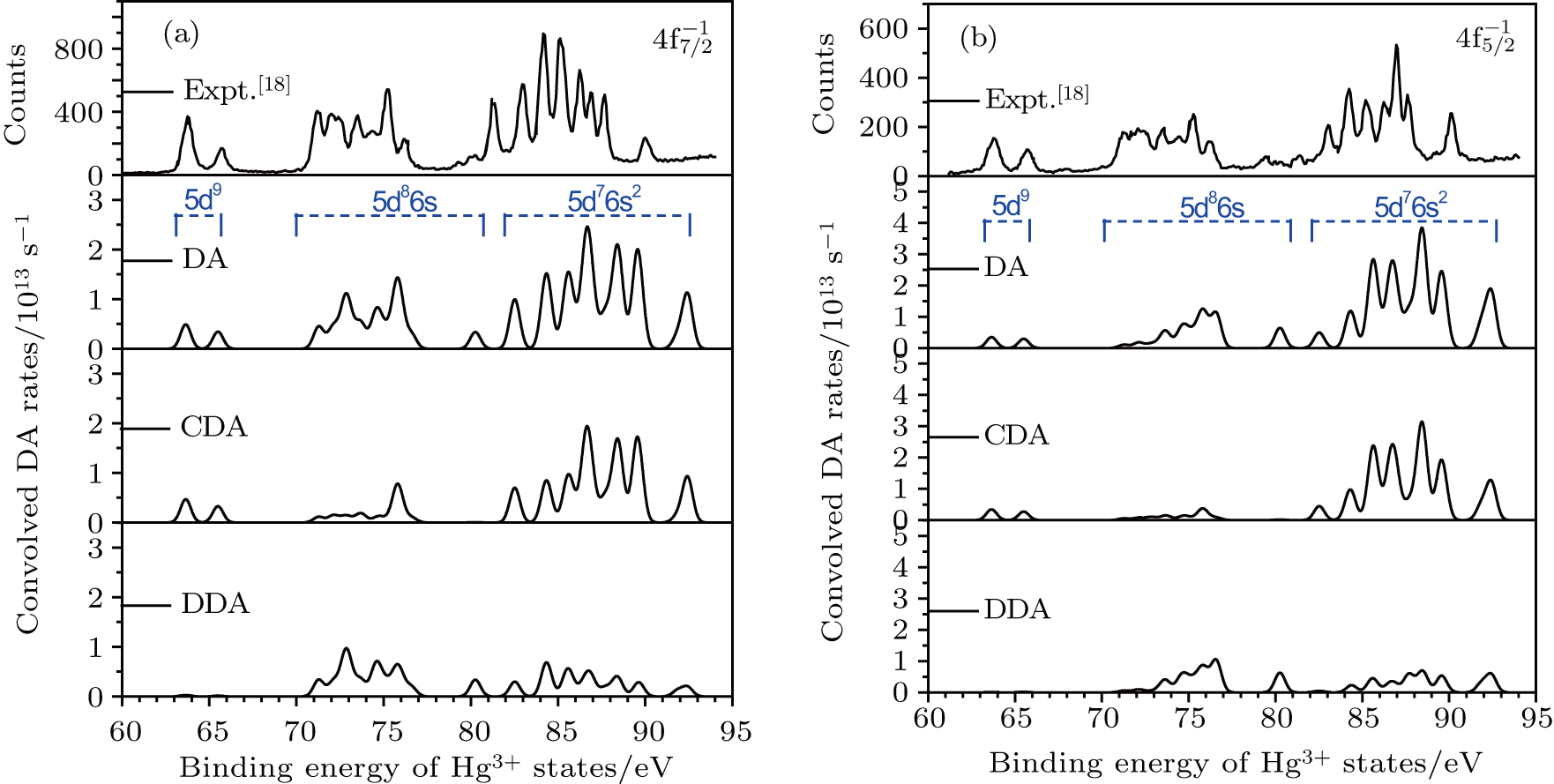 | Fig. 3. (color online) Comparisons between the theoretical and experimental populations of the Hg3+ after the double Auger decay of ionized (a) 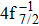 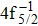 |
The theoretical investigation of the SA and DA decays including the cascade and direct processes, are presented for the Hg 4f−1, based on MCDF method. Due to the computational effort, the important configurations are selected for the main Auger channels. The reference configuration sets are chosen to produce the CI space on the same footing for balancing the electron correlations among the successive singly, doubly and triply ionized mercury. The primary SA electron spectra are in good agreement with experimental measurements. The two-step approximate formulas (KO and SO) derived from the perturbation theory are used to simplify the calculation of the direct DA rates. For the cascade DA decays, the transition channels are determined by the large-scale MCDF calculations and the pathways 4f−1 → 5p55d96s2 → 5d76s2 are dominant, leading to the greatest populations of the highly excited states 5d76s2 of Hg3+, which is peculiar to the cases of the low- and medium-Z atoms such as Ne,[14,31] Ar,[11,13] and Kr.[8,9] Our calculated DA probabilities of 30.60% and 32.26% agree with the experimental values of 30.5% and 32.0%[18] for the 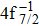
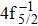
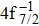
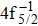
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] |