Project supported by the CNPq, CAPES, and FAPES (Brazilian Agencies).
Project supported by the CNPq, CAPES, and FAPES (Brazilian Agencies).
† Corresponding author. E-mail:
Project supported by the CNPq, CAPES, and FAPES (Brazilian Agencies).
At the second order Douglas–Kroll–Hess (DKH2) level, the B3PW91 functional in conjunction with the relativistic all-electron basis set of valence triple zeta quality plus polarization functions are employed to compute bond lengths, dissociation energies, vertical ionization potentials, and the highest occupied molecular orbital-lowest unoccupied molecular orbital energy gaps of the small iridium clusters (Irn, n ⩽ 8). These results are compared with the experimental and theoretical data available in the literature. Our results confirm the theoretical predictions made by Feng et al. about the catalytic activities of the Ir4 and Ir6 clusters. From the optimized geometries, DKH2 calculations of static electric mean dipole polarizabilities and polarizability anisotropies are also carried out. It is the first time that the polarizabilities of small iridium clusters have been studied. For n ⩽ 4, the mean dipole polarizabilities per atom present an odd–even oscillatory behavior, whereas from Ir5 to Ir8, they decrease with the cluster size increasing. The dependence of the polarizability anisotropy on the structure symmetry of the iridium cluster is verified.
It is known that the transition metals have an incomplete sub-shell in the ground state and that the d sub-shell plays an important role in the properties of the clusters or the bulk materials formed from these elements.[1,2] In the last few years, many theoretical and experimental studies about the group VIII transition metal clusters[3–16] were reported in the literature. The latter studies showed that the stability as well as the catalytic activity and electromagnetic properties are dependent on the size and structure of the cluster. The relationship between the stability and the structure of a cluster is important to understand its catalytic performance.
Iridium is a third row transition metal with a 5d76s2 valence electron configuration. As it is not easily corroded, it is appropriate to be used as the materials that undergo high temperature and pressure.[17,18] Small iridium clusters present catalytic activity on solid support.[19,20] The Hartree–Fock (HF) method and effective core potential (ECP) basis sets were employed to investigate the dependence of the catalytic behavior on the size of iridium clusters (Irn, n = 4, 6, 8, and 10).[21,22] Similar studies for the ruthenium, rhodium, palladium, iridium, and platinum clusters were carried out by Zhang et al. at the density functional theory (DFT) level of theory.[23] From this study, it was shown that the cubic geometries for the iridium clusters are preferred.
As we can note, there are innumerous articles in the literature about the stability and catalytic activity of small iridium clusters, but, to the best of our knowledge, there is no published information about the polarizabilities of these clusters.
Polarizability measures the distortion of the electronic charge distribution of a system due to the presence of an external electric field, and it is useful to understand the electronic properties of clusters. As it is sensitive to the number of electrons and the structure and shape of the cluster, it is extremely valuable in understanding this kind of system.
In earlier researches, it was observed that the mean dipole polarizabilities of adjacent clusters of nickel and niobium often exhibit large variations[24–26] and that these polarizability variations are considerably larger than those obtained for the alkali metal clusters.[27–31] The noble metals (Cu, Ag, and Au), which are sometimes associated with the transition metals, have the d sub-shells fully filled and only one electron in the s valence orbital. In contrast to the nickel and niobium metal clusters, the mean dipole polarizability variations of the copper, silver, and gold clusters[32–34] were verified, in general, to be significantly smaller than those of the lithium and sodium clusters.[35]
For the iridium clusters, no theoretical or experimental results of electric polarizabilities have been reported to date in the literature. Therefore, it is currently only possible to carry out theoretical studies of these properties. For a better understanding of the size dependency and the electronic structure of the ground state iridium clusters up to the octamer, static mean dipole polarizabilities (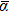
As iridium is a heavy element, it is necessary to consider simultaneously both correlation and relativistic effects on iridium cluster property calculations. So, the computational time rises quickly with the cluster size increasing. To reduce the cost, some strategies have been employed. For example, relativistic ECP along with a valence basis set has been used with success in studying the metal cluster electronic structures. On the other hand, for small metal clusters, relativistic DFT with a high-quality all-electron basis set can be used instead of ECP.
At the second-order Douglas–Kroll–Hess (DKH2) level,[39–41] the Becke three-parameter for exchange and Perdew–Wang 91 for correlation (B3PW91) functional[42,43] in conjunction with the relativistic all-electron basis set of valence triple zeta quality plus polarization functions and one diffuse function of d symmetry (TZP+1d-DKH)[44] as well as with the augmented TZP-DKH (ATZP-DKH)[44] set are utilized in this work. These sets are available at different formats at
First, the geometries of the iridium clusters are optimized at the DKH2-B3PW91/TZP+1d-DKH level and, then, the binding energies, ionization potentials, and HOMO–LUMO energy gaps are computed at the same level of theory. Next, the DKH2-B3PW91/ATZP-DKH polarizabilities are evaluated. It is worth pointing out that for iridium clusters, it is the first time that all electrons have been taken into account in the calculations of these properties and that our results can be useful in checking the accuracy that can be achieved with ECP.
To compute the properties mentioned above, the following equations are used:
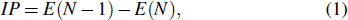 |
 |
 |
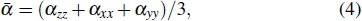 |
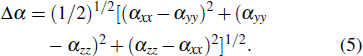 |
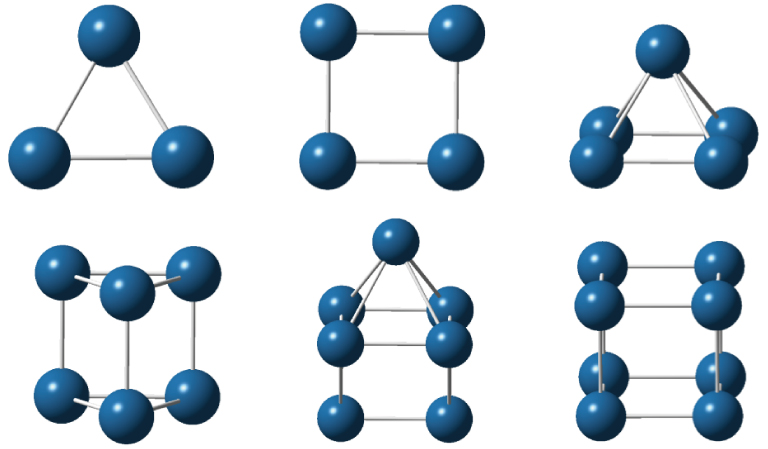
It is known that the number of isomers rises quickly with the iridium cluster size increasing. Therefore, for clusters with five or more atoms, it becomes practically impossible to study all isomers to determine the most stable one. With the purpose of reducing the number of clusters to be investigated, the acquired experience in the construction of metal clusters has been used to choose the possible configurations. Besides, in order to predict correctly the spin states of the iridium clusters it is also indispensable to consider high spin states due to the ground state electronic configuration of the atom (5d76s2). Recently, the ground state geometries and spin states of small iridium clusters were well established through different theoretical approaches.[10,12,13,22,51] The point group symmetries and multiplicities determined in Refs. [10], [12], and [13] are used by us to optimize the geometries of the Irn (n ⩽ 8) clusters with the DKH2-B3PW91/TZP+1d-DKH model. The equilibrium geometries obtained with this procedure are displayed in Fig.
| Table 1.
Calculated values of average cluster bond length (Rave), binding energy (BE), vertical ionization potential (VIP), and HOMO–LUMO energy gap (Egap) for the ground state iridium clusters. . |
For the dimer, there is no experimental data available for the bond length and harmonic vibrational frequency. Nevertheless, Lombardi et al.[53] obtained indirectly 2.23 Å (Pauling’s rule) and 280 cm−1, which are in good agreement with our results (2.190 Å and 291.7 cm−1).
For the trimer, we consider only the D3h symmetry in accordance with Refs. [12] and [13]. In these references, scalar relativistic effects and the B3LYP and BPW91 functionals in conjunction with ECP valence basis sets are employed. In contrast, at the zero order regular approximation (ZORA) level, using the BP86 non-hybrid functional and the frozen-core triple-zeta basis sets plus polarization functions, Ping et al.[10] predicted C2v symmetry for the ground state of Ir3. The predictions obtained from the hybrid functionals are chosen by us because they are more reliable on cluster structure calculations. The Rave value evaluated in this work (2.347 Å) is close to that obtained by Chen and Dixon[12] (2.389 Å).
For the tetramer, once again, whereas the B3LYP and BPW91 functionals predicted the D4h symmetry for the ground state, the BP86 one is converged into the C2 symmetry. The average bond lengths computed with the DKH2-B3PW91/TZP+1d-DKH (2.296 Å) and the relativistic B3LYP/aug-cc-pVDZ-pp (2.348 Å)[12] approaches agree well with each other.
For Irn (n ⩾ 5), our Rave values are systematically smaller than those reported in Refs. [12] and [13] but, in general, in satisfactory agreement with them. Finally, we can note that the DKH2-B3PW91/TZP+1d-DKH average distances of all studied clusters do not exceed the experimental bulk bond length of 2.715 Å.
From the optimized geometries reported in Subsection
For Ir2, the DKH2-B3PW91/TZP+1d-DKH binding energy of 3.699 eV is in excellent accordance with the experimental data of 3.46 ± 0.12 eV[54] and 3.7 ± 0.7 eV.[55] Our BE agrees also with the CBS estimate of 3.799 eV.[12]
Table
Table
For Ir, it is important to note that the experimental VIP of 8.967 eV[57] is in good accordance with our value of 8.690 eV. It suggests that the VIPs reported in this work seem to be reliable.
In Table
In Table
The static polarizability is closely associated with the structural characteristics and electronic properties of clusters. In this article, the static mean dipole polarizabilities, mean dipole polarizabilities per atom, and polarizability anisotropies of small iridium clusters are calculated for the first time and displayed in Table
| Table 2.
Values of static electric mean dipole polarizability ( |
For Ir, the unique value of 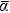
Table 
For n ⩽ 4, the 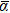
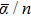
Although the magnitude of the HOMO–LUMO gap is directly related to that of the polarizability, this is not the only dependence, there is the influence of the geometry as well. In fact, there is a competition between these two contributions which determines the polarizability value. It is known that a large HOMO–LUMO energy gap conduces to a chemical stabilization, but the chemical stability of a cluster also depends on highly symmetric 2D and 3D geometries, which contribute to a reduction of the static polarizability.
The above discussion can explain why the mean dipole polarizability per atom of Ir3 is larger than that of Ir6, even though the Ir3 and Ir6 clusters have similar symmetries (D3h). The latter cluster has a more compact structure (3D) than the former one (2D). Similar reasoning explains the polarizabilities per atom, obtained for the Ir4 (2D) and Ir8 (3D) clusters. Going from Ir3 to Ir4, 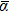
The polarizability anisotropy measures the deformation of the charge distribution due to the presence of an external electric field. A decrease of this property is an indication that the charge distribution is more spherically symmetric.
It is interesting to point out that there is an abrupt fall of the polarizability anisotropy going from the dimer to the trimer (cf. Table
It must be mentioned here that the DKH2-B3PW91/ATZP-DKH polarizability anisotropy of Au3 (122.39 a.u.) reported in Ref. [34] is larger than that of Ir3. The main reason for this significant difference is that, unlike Ir3, it belongs to the C2v point group, i.e., Au3 has a more open structure. As the gold clusters with n ⩾ 4 are planar, differently from the iridium clusters, their Δα values increase with the number of atoms increasing.[34]
In this article, the DKH2-B3PW91/TZP+1d-DKH model has been employed to calculate geometries, binding energies, vertical ionization potentials, and HOMO-LUMO energy gaps of small iridium clusters.
In general, the DKH2-B3PW91/TZP+1d-DKH bond distances are in good agreement with results reported previously.[10,12] In particular, for Ir2, our result is only 0.04 Å smaller than an experimental value found in the literature.[53]
Except for Ir5 and Ir7, the DKH2-B3PW91/TZP+1d-DKH binding energies agree well with theoretical values obtained from a higher level of theory [CCSD(T)/CBS].[12] Like BE, the BE/n increases with the cluster size increasing. The binding energies per atom indicate that the even-numbered clusters are slightly more stable than the odd-numbered ones. From tetramer to octamer, the vertical ionization potentials exhibit an even–odd oscillating feature, indicating one more time that the even-numbered clusters are more stable.
From the HOMO–LUMO relativistic results reported in this work, we verify that Ir4 and Ir6 are the most reactive clusters and that Ir8 presents low chemical activity. These findings confirm the predictions made by Feng et al.[22] about the catalytic and non-catalytic activities of the tetramer, hexamer, and octamer, respectively.
As the DKH2-B3PW91/ATZP-DKH polarizabilities calculated in this work are unique, they can be used to calibrate upcoming DFT and/or ab initio calculations. For n ⩽ 4, the mean dipole polarizabilities per atom display an odd–even oscillation. It is the inverse of that observed for the HOMO–LUMO energy gaps. It is in accordance with the chemical intuition. As expected, the largest 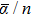
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] |