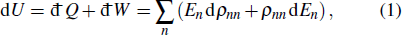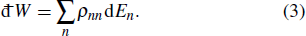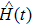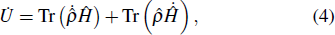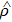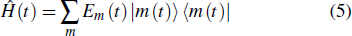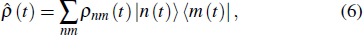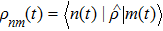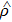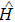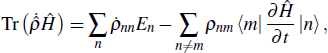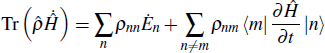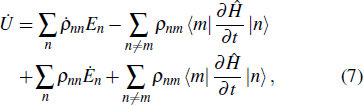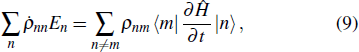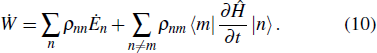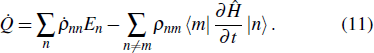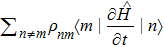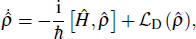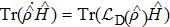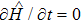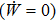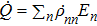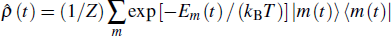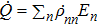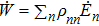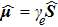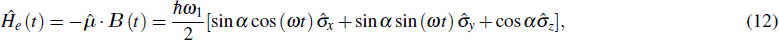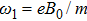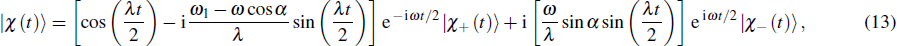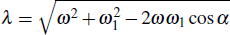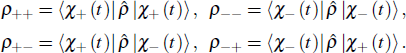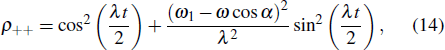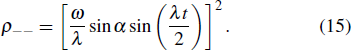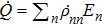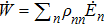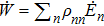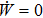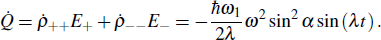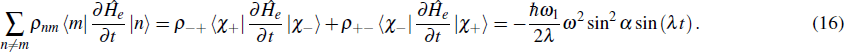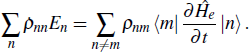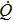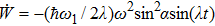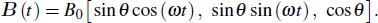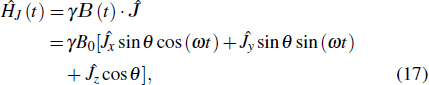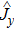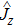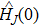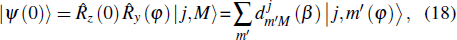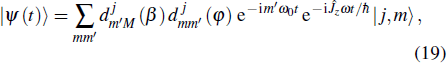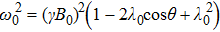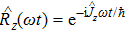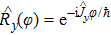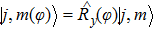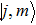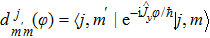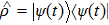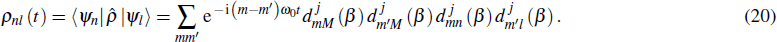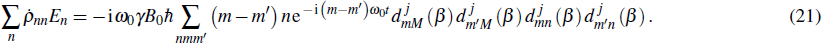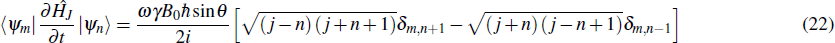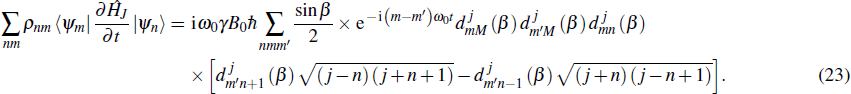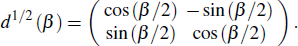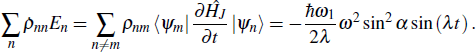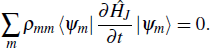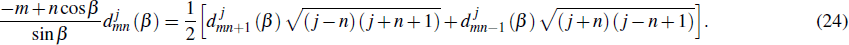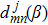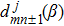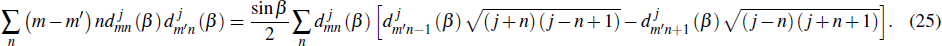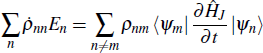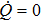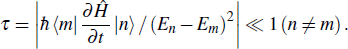Cite this Article
Su Shanhe, Chen Jinfu, Ma Yuhan, Chen Jincan, Sun Changpu. The heat and work of quantum thermodynamic processes with quantum coherence. Chinese Physics B, 2018, 27(6): 060502  
Permissions
The heat and work of quantum thermodynamic processes with quantum coherence
Su Shanhe1, 2, Chen Jinfu1, 3, Ma Yuhan1, 3, Chen Jincan2, Sun Changpu1, 3, †
Beijing Computational Science Research Center, Beijing 100193, China
Department of Physics, Xiamen University, Xiamen 361005, China
Graduate School of the Chinese Academy of Engineering Physics, Beijing 100193, China

 

† Corresponding author. E-mail: cpsun@csrc.ac.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 11421063, 11534002, and 51776178) and the National Key Basic Research Program of China (Grant Nos. 2012CB922104 and 2014CB921403).

Abstract

Energy is often partitioned into heat and work by two independent paths corresponding to the change in the eigenenergies or the probability distributions of a quantum system. The discrepancies of the heat and work for various quantum thermodynamic processes have not been well characterized in literature. Here we show how the work in quantum machines is differentially related to the isochoric, isothermal, and adiabatic processes. We prove that the energy exchanges during the quantum isochoric and isothermal processes are simply depending on the change in the eigenenergies or the probability distributions. However, for a time-dependent system in a non-adiabatic quantum evolution, the transitions between the different quantum states representing the quantum coherence can affect the essential thermodynamic properties, and thus the general definitions of the heat and work should be clarified with respect to the microscopic generic time-dependent system. By integrating the coherence effects in the exactly-solvable dynamics of quantum-spin precession, the internal energy is rigorously transferred as the work in the thermodynamic adiabatic process. The present study demonstrates that the quantum adiabatic process is sufficient but not necessary for the thermodynamic adiabatic process.

PACS: 05.70.-a;05.70.Ln;07.20.Pe;
Keyword:heat and work;thermodynamic adiabatic process;quantum coherence;
1. Introduction

Thermodynamics is reputed to have the ability to deal with the energy transfer and work utilizing an extremely small number of variables. Numerous quantum devices that are related to harnessing energy focus on pioneering concepts and unexplored mechanisms. They are exemplified by artificial photosynthesis,[1–3] quantum information heat engines,[4–7] quantum thermodynamic cycles,[8–10] and photovoltaic cells.[11,12] The design of an improved quantum-inspired energy converter compels us to clarify the heat exchange and work done from microscopic mechanisms, and study the emergence of thermodynamic behaviors within quantum mechanical systems.

According to the first law of thermodynamics, the infinitesimal internal energy variation of a quantum system is

where En and ρnn are the eigenenergy and the occupation probability of the n-th eigenstate, respectively. The change in the internal energy dU can be written in terms of a perfect differential. The symbol đ indicates that the heat Q and work W are path-dependent. The heat exchange đQ and the work done đW during an infinitesimal thermodynamic process are often identified as[13,14]
and
These imply that the heat transfer between the quantum system and the heat bath induces the rearrangement of the occupation probabilities, while the work has to be done by changing the generalized coordinates of the system.[15,16] However, these forms of identification are not strictly comfortable with rigorous mathematical proof. Questions inevitably arise when one is faced with a system undergoing different thermodynamic processes studied commonly. In fact, it may induce doubts over whether the above definitions of the heat and work are applicable for any process.

Based on the dissipative master equation, the heat and work relevant to the open quantum system with time-dependent Hamiltonian were introduced in the pioneering research of Alicki.[17,18] Kosloff et al. implemented Alicki’s formulas and systematically studied quantum heat engine cycles working with harmonic oscillators and spins.[19–21] Here, writing the heat and work in term of the systemic instantaneous orthonormal basis, we show that quantum coherence characterized by the off-diagonal elements of the density matrix stimulates additional energy changes in thermodynamic processes. The quantum effects make the heat and work of quantum isochoric, quantum isothermal, and thermodynamic adiabatic processes different from one another. The exactly-solvable dynamics of high-spin precession will be used to prove that quantum coherence guarantees the thermodynamic adiabatic evolution of a time-dependent system.

2. Expressions of heat and work in quantum thermodynamic processes

For a general quantum system, an external driving field gives rise to a time-dependent Hamiltonian 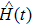. According to the microscopic description of the first law of thermodynamics, the change in the internal energy of the system can be split into two separate parts, i.e.,

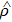
where the superposed dot denotes the time derivative and is the density operator corresponding to the ensemble.[17,22,23]

Let {|m(t)⟩, m = 1, 2, …} be a complete instantaneous orthonormal basis of , we can write the Hamiltonian and the density operator in a matrix form, that is

and
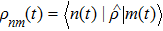
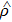
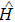
where Em(t) is the eigenvalue of the state |m(t)⟩ at any particular instant and represents the density matrix element. For the sake of simplicity, time t is omitted in the notation. Note that the off-diagonal element ρnm(n ≠ m) exists, meaning that and do not have a common orthonormal basis. With the help of Eqs. (5) and (6), we have
and
(see Appendix A for detail). The rate of change of the internal energy becomes
which are classified into four different categories. The second and fourth terms representing the quantum coherence have the same magnitude but different signs. They would cancel each other resulting in the consistency between Eq. (7) and Eq. (1). However, we find that the connection between the quantum coherence and the infinitesimal increments of the heat and work exists. For a closed system subjected to a time-dependent force, the unawareness of the quantum coherence may violate the first law of thermodynamics.

In thermodynamics, an adiabatic process in a closed system occurs when the transfer of heat and matter between the thermodynamic system and its surrounding is avoided. The evolution of the density operator during the adiabatic process is unitary. Based on the Liouville–von Neumann equation[24]

and the time derivative of the density matrix formula, we have (see Appendix B for detail)
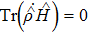
which indicates that . According to the first law of thermodynamics, the internal energy in an adiabatic process is transferred only as work, and the rate of work performed in this process is given by

The rate of the heat transfer should have the following form

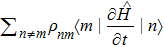
Only when the quantum coherence, represented by , is considered, is the absence of the heat loss to the surroundings in the adiabatic process guaranteed. The above descriptions of the heat and work are compatible with Alicki and Kieu’s definitions and can be generalized to open quantum system dynamics.[17,25]

For the combined system bath scenario, the quantum master equation is described explicitly as

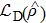
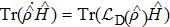
where is the dissipative superoperator responsible for the interaction of a quantum system with its environment. Straightforwardly, we obtain , which demonstrates that all dissipative parts due to the heat exchange are contained in Eq. (11). Equations (10) and (11) give the general definitions of the heat and work in quantum thermodynamic processes. The first part of Eq. (10) indicates that the work done on or by a system can be obtained through the redistribution of the energy eigenvalues En. The first term in Eq. (11), on the other hand, shows that the heat transfer is related to a change in the occupation probabilities ρnn. The second terms in Eqs. (10) and (11) imply that both the heat transfer and the work done in a microscopic process are closely related to the quantum coherence. Considering other specific types of thermodynamic processes, we will find that the heat transfer rate and the work flux may have different characteristics.

When the external field is fixed and the quantum system is put into contact with a thermal bath at a certain temperature, an isochoric evolution can be carried out. Since 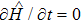and the eigenvalues of the Hamiltonian operator En remain constant throughout the isochoric process, no external work is performed 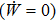, leading to the sole change in the internal energy due to the heat exchange. The heat transfer rate between the system and the thermal bath under this condition can be calculated as 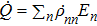, which is simply depending on a change in the population of the microstates.

The quantum isothermal processes typically occur when a system is kept in contact with a thermal bath. The system is capable of performing positive work to the outside, and meanwhile absorbs heat from the bath. Both the eigenvalues En and the occupation probabilities ρnn need to be changed simultaneously. This operation will occur slowly enough to allow the system to remain in equilibrium with the thermal bath at every instant. The density operator at thermal equilibrium is characterized by thermally distributed populations in the quantum states

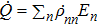
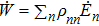
with Z = ∑m exp[−Em(t)/(kBT)] being the canonical partition function. Since the system approaches thermal equilibrium without a typical relaxation time due to the bath-system interactions, quantum coherence vanishes, i.e., ρnm = 0(n ≠ m). The heat transfer rate and the work flux in the quantum isothermal processes can be expressed as and , respectively. Because the adiabatic process does not require the second terms in Eqs. (10) and (11) to be a zero value, the general expressions of the rates of the work performed and the heat transfer are different from the counterparts in the isothermal and isochoric processes. Examples of illustrating the valid arguments of the above discussion will be given in the following sections.

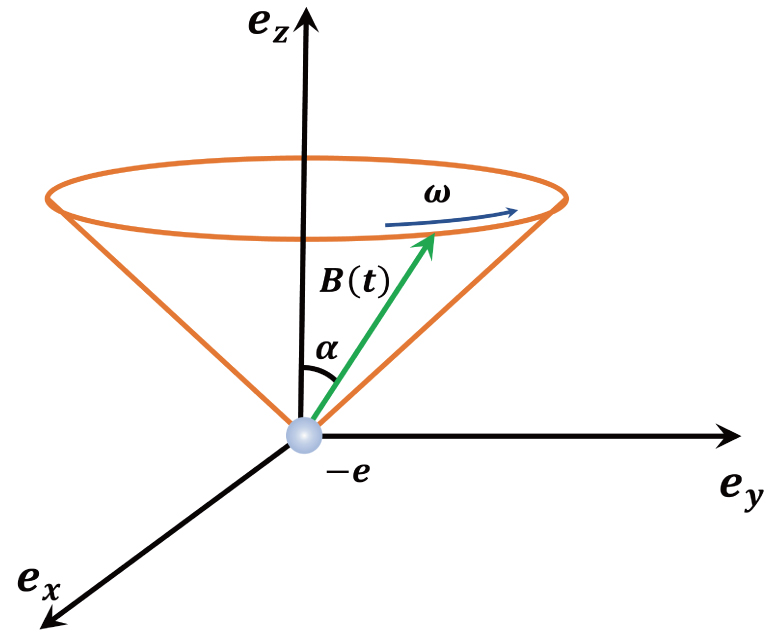
3. The adiabatic evolution of a two-level model in a magnetic field

It is instructive to look at an electron with charge −e and mass m located at the origin of three-dimensional space (as shown in Fig. 1). The dipole moment of the electron is proportional to its gyromagnetic ratio γe = −e/m and spin angular momentum 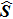, i.e., 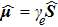. When a magnetic field B(t) = B0[sin α cos (ωt)ex + sin α sin (ωt)ey + cos α ez] is applied, the electric dipole of the electron interacts with the field and the time-dependent Hamiltonian of the system is[26]

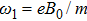
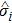
where ; (i = x, y, and z) are the usual Pauli spin matrices; and ħ equals the Planck constant divided by 2π.

Fig. 1. (color online) An electron in the presence of a magnetic field whose magnitude B0 is a constant, but whose direction rides around at an angular velocity ω on the tip of a cone of opening angle α.

The wave function for the two-state system is a linear combination of the normalized eigenvectors |χ+ (t)⟩ and |χ−(t)⟩, i.e.,

where
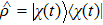
(see Appendix C for detail). The density matrix operator can be written as . Taking the matrix elements, we obtain

It is obvious that ρ++ and ρ−− are the probabilities of being in the spin up and spin down states along B(t) and are, respectively, given by

and

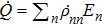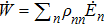Most of the existing literature studied the thermodynamic properties of the quantum systems with time-independent Hamiltonian. Thus, the heat exchange rate and the work flux in a thermodynamic process can be simplified as and . These indicate that only the population transfer results in the microscopic realization of the heat exchange, while the work merely depends on the energy change generated by the external field. However, for the electron-spin system driven by a rotating magnetic field, the eigenvalues corresponding to the instantaneous eigenstates |χ+(t)⟩ and |χ−(t)⟩ are time independent (see Appendix C for detail). If the work flux in the adiabatic evolution process remains being computed by 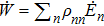, we have 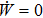. It means that no work can be done by the magnetic field B(t), which is an apparent paradox. In addition, according to the time derivative of ρ++ and ρ−− from Eqs. (14) and (15), the heat exchange rate

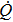
As is a non-zero value, it is a paradox that there exists heat transfer between the system and the environment in the thermodynamic adiabatic process.

In the present studies, we emphasize that the quantum coherence effects are necessary for reclaiming the validity of the first law of thermodynamics when a quantum system with time-dependent Hamiltonian is considered. Making use of Eq. (13) and taking the off-diagonal elements of the density operator, one readily obtains

It is observed that
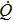
According to this and Eq. (11), we ensure that the heat transfer rate of the two-state system in the adiabatic evolution process equals zero and the corresponding power generated by the external field .

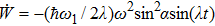
4. Test of the thermodynamic adiabatic process via the exactly-solvable dynamic of high-spin precession

In this section, we consider a neutral particle with a magnetic moment and arbitrary spin j in a harmonically-changing external magnetic field

The magnetic field rotates around the z axis with frequency ω and is inclined at a constant angle θ. The systemic Hamiltonian is time-dependent and is given by
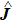
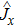
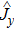
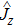
where γ is the coupling parameter and is the total angular momentum vector. The operators , , and represent three Cartesian components of the angular momentum. Learning the thermodynamic behavior of high-spin precession faces a demand with the exact solution for the wave function. The Schröinger equation with the time-dependent Hamiltonian is usually difficult to deal with. However, it can be reduced to a Schröinger-like equation with a time-independent effective Hamiltonian by invoking quantum rotation transformation in angular momentum theory.[27]

If the system is placed initially in an instantaneous eigenstate of 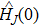, i.e.,

the exact solution of the time-dependent wavefunction becomes
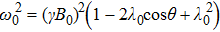
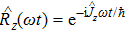
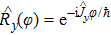
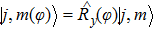
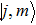
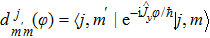
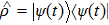
where λ0 = ω/γB0; ; and β = θ − φ. In Eq. (18), the operators and are the rotation operators, and with (m = j, j − 1, …, −j) are the rotations of the standard angular momentum basis . represents an element of Wigner’s d-matrix. Details of the algorithm are given in Appendix D. The wavefunction |ψ(t)⟩ is a linear combination of the eigenstates |ψm⟩. As the density operator , we can explicitly carry out its matrix elements

Similar to the previous model, the dynamic evolution of high-spin precession can also be visualized as an adiabatic process in which no heat is gained or lost by the system. Accordingly, using Eq. (11), we will show that the high-spin system is hardly thermally isolated unless the quantum coherence is considered. From Eqs. (11) and (20), we immediately have

Knowing that

and the relation ω sin θ = −ω0 sin β, we can write the second term of Eq. (11) as

In the spin 1/2 case, the matrix representation of Wigner d-function

If we substitute ω0 → λ, γB0 → ω1, and φ → α, it is not difficult to work out that
This formula is completely analogous to the result obtained by the two-level model moving in an adiabatically rotating magnetic field. As an interesting application of the exact explicit solutions of the Hamiltonian in Eq. (17), we will show that the spin-precession processes are thermodynamically adiabatic regardless of the spin quantum numbers of any particles. The proof is straightforward, which can be done by substituting Eqs. (21) and (23) into Eq. (11).

When m = m′, we have

Only the terms with m ≠ m′ need to be considered in the computation. In the quantum theory of angular momentum, the recursion relation for Wigner’s d-matrix implies that[28–30]

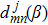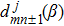Combining the relation between and and the usual index transformation, one can derive the following invariant sum which gives the coupling rules relating to the direct product of two rotation matrices

The detail calculations are given in Appendix E. Applying the invariant sum to Eqs. (21) and (23), we can verify that
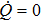
for an instantaneous state. As the heat exchange rate , the spin system exchanges no mass or heat energy with its environment. The change in its internal energy is merely due to the work done by the external magnetic field. Once again, the analysis demonstrates that the unitary evolution of a closed system with time-dependent Hamiltonian is equivalent to a thermodynamic adiabatic process when the quantum coherence is taken into account.

If a system starts from an eigenstate of the initial Hamiltonian, the quantum adiabatic theorem states that the system will remain in the corresponding instantaneous eigenstate of the final Hamiltonian when a given perturbation acting on it is slow enough.[31,32] The adiabatic approximation holds when the time derivative of the Hamiltonian is extremely small and the dimensionless adiabatic parameter

However, the above analysis shows that the thermodynamic adiabatic processes do not require the quantum adiabatic approximation to be satisfied. A quantum adiabatic process certainly results in a thermodynamic adiabatic process, but not all thermodynamic adiabatic processes are due to the quantum-mechanical adiabatic processes.

5. Conclusions

In summary, we found that the heat and work in microscopic processes are closely related to the transition between different quantum states. The energy exchanges during the quantum isochoric and isothermal processes are simply depending on the change in the eigenenergies or the probability distributions. However, for a closed system with time-dependent driving, the unitary evolution is equivalent to a thermodynamic adiabatic process only when the quantum coherence is taken into account. Under this consideration, one can ensure that no heat is lost to or gained from the surroundings in the case of quantum-spin precession. The microscopic expressions for thermodynamic quantities are applicable to both the thermal equilibrium case and the nonequilibrium case.

Reference
[1] Chen H Wang X Fang A Li H 2016 Chin. Phys. 25 098201
[2] Qin M Shen H Z Zhao X L Yi X X 2017 Phys. Rev. 96 012125
[3] Wang X Li H Zhang P Li F 2013 Chin. Phys. 22 117102
[4] Boyd A B Crutchfield J P 2016 Phys. Rev. Lett. 116 190601
[5] Anjaria K Mishra A 2017 Chin. Phys. 26 100507
[6] Zwick A Ávarez G A Kurizki G 2016 Phys. Rev. Appl. 5 014007
[7] Horowitz J M Esposito M 2014 Phys. Rev. 4 031015
[8] Wang H Wu G 2012 Chin. Phys. 21 010505
[9] He J Xian H Zheng J 2012 Chin. Phys. 21 050303
[10] Xu D Wang C Zhao Y Cao J 2016 New. J. Phys. 18 023003
[11] Svidzinsky A A Dorfman K E Scully M O 2011 Phys. Rev. 84 053818
[12] Su S H Sun C P Li S W Chen J C 2016 Phys. Rev. 93 052103
[13] Quan H T Liu Y Sun C P Nori F 2007 Phys. Rev. 76 031105
[14] Lin B Chen J 2003 Phys. Rev. 67 046105
[15] Wang J Ye Z Lai Y Li W He J 2015 Phys. Rev. 91 062134
[16] Wang H He J Wang J Wu Z 2016 J. Appl. Phys. 120 154303
[17] Alicki R 1979 J. Phys. A: Math. Gen. 12 L103
[18] Alicki R 2016 Entropy 18 210
[19] Kosloff R Rezek Y 2017 Entropy 19 136
[20] Rezek Y Kosloff R 2006 New. J. Phys. 8 83
[21] Geva E Kosloff R 1992 J. Chem. Phys. 97 4398
[22] Boukobza E Tannor D J 2006 Phys. Rev. 74 063823
[23] Hossein-Nejad H O’Reilly E J Olaya-Castro A 2015 New J. Phys. 17 075014
[24] von Neumann J 1955 Mathematical foundations of quantum mechanics Princeton Princeton University Press 12 15
[25] Kieu T D 2006 Eur. Phys. J. 39 115
[26] Griffiths D J 2005 Introduction to quantum mechanics 2 New Jersey Prentice Hall 373 374
[27] Sun C Zhang L 1995 Phys. Scr. 51 16
[28] Biedenharn L C James D L 1984 Angular momentum in quantum physics Cambridge Cambridge University Press 53
[29] Varshalovich D A Moskalev A N Khersonskii V K M 1988 Quantum theory of angular momentum Singapore World Scientific 12 15
[30] Feng X M Wang P Yang W Jin G R 2015 Phys. Rev. 92 043307
[31] Berry M V 2009 J. Phys. A: Math. Theor. 42 365303
[32] Sun C P 1988 J. Phys. A: Math. Gen. 21 1595