Project supported by the Natural Science Foundation of Hebei Province, China (Grant Nos. A2012203174 and A2015203387) and the National Natural Science Foundation of China (Grant Nos. 10974169 and 11304270).
Project supported by the Natural Science Foundation of Hebei Province, China (Grant Nos. A2012203174 and A2015203387) and the National Natural Science Foundation of China (Grant Nos. 10974169 and 11304270).
† Corresponding author. E-mail:
Project supported by the Natural Science Foundation of Hebei Province, China (Grant Nos. A2012203174 and A2015203387) and the National Natural Science Foundation of China (Grant Nos. 10974169 and 11304270).
We comprehensively investigate the nontrivial states of an interacting Bose system in a cosine potential under the open boundary condition. Our results show that there exists a kind of stable localized state: edge gap solitons. We argue that the states originate from the eigenstates of independent edge parabolas. In particular, the edge gap solitons exhibit a nonzero topological-invariant behavior. The topological nature is due to the connection of the present model to the quantized adiabatic particle transport problem. In addition, the composition relations between the gap solitons and the extended states are also discussed.
Recently, the topological properties in one-dimensional (1D) superlattices have attracted tremendous research attention. Besides the topological states of some well known models such as the Su–Schrieffer–Heeger model,[1,2] the Kitaev–Majorana chain[3] has also been investigated theoretically; topological states were also realized experimentally with the incommensurate superlattices in photonic crystals[4] and cold atoms.[5,6] In particular, the better tunability of particle hoping and interactions in cold atoms offer a clean and parameter-controllable platform to investigate 1D topological insulators.[7] It is well known that, in the mean field level, the interactions between Bose particles in low temperature can result in significant nonlinearities.[8–10] Nonlinearity in turn has significant effects on their stabilities.[11–13] For example, the instabilities are responsible for the formation of the train of localized filaments[8] and are closely related to the breakdown of the superfluidity.[14] The topological properties of an interacting Boson system has been studied in one-dimensional bichromatic superlattices.[15] The nontrivial edge solitions were found on the boundaries of the lattice and its topological properties were illuminated by Chern numbers of the nonlinear Bloch bands defined in the extended two dimensional parameter space. However, finding the topological states in a simple superlattice is still an important issue.
Here we show that the topological gap solitons can exist in a simple cosine potential. Their topologically nontrivial properties are due to the introduction of a modulation phase in the periodic potential well, which provides an additional dimension. We explain with numerical analysis how these states can be induced by the edge parabola. The stabilities and composition relations of the gap solitons are also discussed. The paper is organized as follows. In Section
We consider a weakly interacting Bose gas loaded in a 1D periodic optical lattice with periodic potential V(x) = vcos(2πx/a + δ). Here v is the potential strength, a is the period of the potential, and δ is an arbitrary phase. On the mean field level, the above system can be well described by the following nonlinear Schrödinger equation
From the Schrödinger equation (
Beside some special cases, there are no analytical solutions for the two equations [Eqs. (
The nonlinear equations [Eqs. (
To understand the origin of the edge states, we have plotted the periodic potentials V(x) (red dashed lines) in Fig.
It has been pointed out that the nonlinear periodic system can host a special kind of waves, namely gap solitons, which are spatially localized wave packets with chemical potentials in the linear band gaps.[21] It has also been found that the gap solitons and the nonlinear Wannier functions match very well. The match gets even better as the periodic potential becomes stronger.[10,22] The excellent match between the gap solitons and the nonlinear Wannier functions suggests that the gap solitons can be approximated by the orbital wave functions of a unit cell since the orbital wave functions can be taken as Wannier functions when the periodic potential is stronger. Here, the formations of the stable edge state are due to the linear spreading from the kinetic energy and the repulsive interaction compensated by the confinement of a roughly triangular potential well. So the edge states can be called edge gap solitons. However, while the spatially localized wave packets form in the parabola away from the boundary, these states are called the gap solitons.
For the edge gap soliton, the wave function localizes in the boundary and has a long tail. This is due to the wave function overlap between the edge gap soliton and the near gap soliton. For the edge gap soliton Ψ8 shown in Fig.
For the edge gap solitons Ψ16, its chemical potential lies in the second band gap. It is natural to estimate that the wave function develops from the first excited state of the right parabola and the wave function in a cell with a node. However, the wave function shows only one peak, which is the same as that of the state Ψ8. This is due to the fact that the parabola for Ψ16 is closer to the right wall than the parabola for Ψ8 in the left side. It gives a strong confinement of the particles. So the chemical potential of Ψ16 is higher than that of Ψ8.
The linear stability is studied according to the following standard procedure. Since the unstable solution is sensitive to a small perturbation, one can add a small perturbation ΔΨ(x, t) to a known stationary solution Ψ(x) of the nonlinear Schrödinger equation (
 |
The stabilities of the edge gap solitons are investigated in Fig.
The appearance of edge states in the current problem is attributed to the nontrivial topological properties of bulk systems. In Fig. 
The gapless edge states are related to the topological property of the system. The topological structure is characterized by the topological invariant which can be characterized by the Chern numbers of the occupied energy bands.[23,24] For the current nonlinear periodic model, the introduction of the potential shift δ makes the potential V(x) change periodically with δ. The eigenvector ψnk and eigenvalue Enk of the Bloch equation [Eq. (
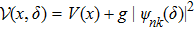
On the other hand, the above model is natural to relate the adiabatic variations of the potential in time V(x, t), i.e., the quantized adiabatic particle transport problem. For simplicity of the discussion, the particle in a band is viewed as a set of charge localized in the center of the Wannier functions. With the increase of the time, the potential will translate its position and the particle will move with the potential. Although the Wannier function recovers its original shape after a cycle of the potential, its position or a particle has slid by a lattice-constant. The average particle current over a time cycle is the Chern number.[25,26]We follow the method in Ref. [27] to perform the computation of the Chern number directly. We find that the Chern numbers for the Boson in the three sub-bands are 1, −2, and 1, respectively, for both the linear (g = 0) and nonlinear (g = 300) cases.
As discussed in Refs. [10], [22], [28], and [29], gap solitons develop in the linear band gaps and originate from the bound states of a single parabola. So they can be divided into different families according to the locations of the band gaps. On the other hand, the nonlinear Bloch band can be viewed as a lifted linear Bloch band by increasing the nonlinear interaction. However, the linear Bloch band can be viewed as an evolution from the discrete energy levels of an individual parabola. In particular, the gap solitons match the Wannier function well when the periodic potential is strong. Therefore, the gap solitons and nonlinear Bloch waves should share certain common features. This is called the ‘composition relation’. By numerical analysis, an almost perfect match is found between the nonlinear Bloch waves and the gap solitons within a single unit cell of V(x). The good matches give strong evidences to verify that gap solitons are the building blocks of the nonlinear Bloch waves. The issue is whether the composition relation is still valid under the open boundary condition.
Under the open boundary condition, the system still exists in extended states. As shown in Fig.
We solve the nonlinear Schrödinger equation [Eq. (
The extended state Ψ1(x) in Fig.
In summary, we have explored the nontrivial states of the interacting Bosons confined in a 1D cosine potential under the open boundary condition. Our study reveals that a kind of wave exists in this system: edge gap solitons. The localized waves originate from the edge parabolas and exhibit nontrivial topological natures. We find that the problem connects to the quantized adiabatic particle transport. With the linear stability analysis, it is found that the stable edge gap solitons can exist near the bottom of the linear band gap. The numerical results verify that the composition relation remains correct under the open boundary condition. Edge gap solitons are thus the fundamental building blocks to extend states. It is expected that the results will be useful for observing topological phases by using a 1D Bose system.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] |






