Project supported by the National Key Basic Research and Development Program of China (Grant No. 2016YFA0301802) and the National Natural Science Foundation of China (Grant Nos. 11504165, 11474152, and 61521001).
Project supported by the National Key Basic Research and Development Program of China (Grant No. 2016YFA0301802) and the National Natural Science Foundation of China (Grant Nos. 11504165, 11474152, and 61521001).
† Corresponding author. E-mail:
Project supported by the National Key Basic Research and Development Program of China (Grant No. 2016YFA0301802) and the National Natural Science Foundation of China (Grant Nos. 11504165, 11474152, and 61521001).
A quantum algorithm provides a new way in solving certain computing problems and usually faster than classical algorithms. Here we report an implementation of a quantum algorithm to determine the parity of permutation in a single three-dimensional (3D) superconducting transmon qutrit system. The experiment shows the capacity to speed up in a qutrit, which can also be extended to a multi-level system for solving high-dimensional permutation parity determination problem.
Quantum computation has been fascinating as the great potential power in solving the computational tasks more efficiently than the classical computer.[1] Over the past few decades, lots of quantum algorithms[2,3] have been proposed and provide a new vision in solving certain problems. Most of the quantum algorithms can realize quantum intrinsic parallel computation in a system with at least two entangled qubits, e.g., the Deutsch-Josza algorithm,[4] Shor’s factoring algorithm,[5] Grover’s searching algorithm,[6] and so on.[7–10] Generally, superposition and entanglement are considered as the main sources of acceleration of quantum computation. Mark Howard et al.[11] proposed that quantum contextuality[12] also plays an important role in determining the power of quantum computing; although the origin of the speed-up in quantum algorithms has been studied a lot, it is still not completely clear.[13] Recently, an interesting and simple quantum algorithm[14,15] is proposed to realize computational speed-up and the implementation requires only a single qutrit. This quantum algorithm can determine the parity of permutation twice as fast as the classical algorithm. It has been experimentally demonstrated in different types of quantum systems, including the nuclear magnetic resonance systems[14,15] and optical systems.[16,17] As the single qutrit is the smallest system[18] where the quantum contextuality can be observed, these experiments support the points that the entanglement is not necessary in all quantum speed-up, and the contextuality may be the origin of the speedup in this algorithm.
As one of the most promising candidates for building a quantum computer, superconducting quantum circuits can also be used to realize this quantum algorithm. In superconducting quantum circuits, people usually use the lowest two levels of the transmon to serve as a qubit for designing quantum computation algorithms. However, it is well known that a single superconducting transmon actually possesses multiple energy levels and can be treated as an artificial atom. A multi-level system, which corresponds to a large Hilbert space, can not only be used to design a Hamiltonian for quantum simulations,[19,20] but also store or encode more quantum information,[21–25] so that it can perform a much more complicated quantum algorithm than a qubit. In this paper, we demonstrate the permutation algorithm in a superconducting 3D transmon qutrit, which is the simplest case to show the computational speed-up. Our scheme holds the promise to extend the permutation algorithm to N dimensions with N levels or N qubits, providing a platform for studying the origin of speed-up in a superconducting quantum circuit system.
Considering there is a black box to realize cyclic permutations, in the three objects case, the six different permutations can be defined in the set of 1, 2, 3, which are (1, 2, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1), (2, 1, 3), and (1, 3, 2). The parity of these permutations can be categorized as even or odd, depending on whether the number of the performed exchange operations would be even or odd. Therefore, the first three are even permutations and the last three are odd permutations. The computational task is to determine the parity of the cyclic permutations realized by the black box after query. In the quantum setting, the input and the output are the qutrit state |m⟩, where m = 0, 1, 2 denote the three energy levels of the qutrit. The permutation can be considered as a function y = f(x) which maps the input x ∈ 0, 1, 2 to the output y ∈ 0, 1, 2. These permutation functions can be realized by the unitary transformation acted on the qutrit. The six permutation functions written in Cauchy’s two-line notation and the corresponding unitary transformations are given in the Eq. (
In the classical scheme, to determine the parity of permutations requires the query on the black box (function) for at least two different inputs. However, the quantum permutation algorithm has been proposed to solve this problem with only one step of query. In the quantum permutation algorithm, the initial state is prepared in the ground state |0⟩ of the qutrit. By doing a qutrit quantum Fourier transformation (QFT)[1] defined as
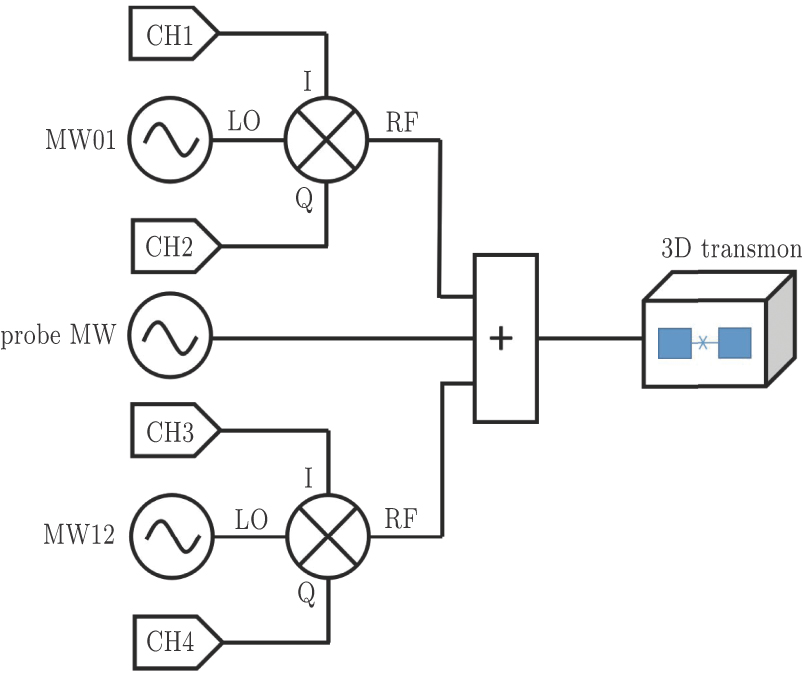
The experiment system is a superconducting transmon embedded in a 3D aluminum cavity. The main purpose of the cavity in our experiments is to provide a clean electromagnetic environment and to serve as a convenient tool for manipulation and measurement.[19,26] The sample is an Al–AlOx–Al Josephson junction about the size of 150 nm × 150 nm connected to two aluminum pads, which is fabricated on a sapphire substrate. The whole pattern is fabricated with e-beam lithography and double angle e-beam evaporation technique. Here we use the lowest three energy levels of the transmon, namely |0⟩, |1⟩, and |2⟩, as a qutrit system. From spectroscopy measurement, we obtain the transition frequency between |0⟩ and |1⟩ is ω01 = 2π × 7.1572 GHz, and the transition frequency between |1⟩ and |2⟩ is ω12 = 2π × 6.8154 GHz. From these transition frequencies, we can calculate the anharmonicity of the qutrit α = 2π × 341.8 MHz. The relatively large anharmonicity ensures that the manipulation applied on any two level transitions would not cause other spurious excitations. The resonant frequency of the 3D cavity is ωc = 2π × 9.0524 GHz. The coupling strength between the qutrit and the cavity is about 2π × 50 MHz. In our design, the detuning between the qutrit transition frequency and cavity frequency are much larger than the coupling strength between the qutrit and the cavity, thus the system works in the dispersive region.[27] The energy relaxation time T1 of the qutrit is about 10 μs and the decoherence time T2 measured from the Ramsey experiment is about 8 μs. The device is cooled in a cryogen-free dilution refrigerator to a base temperature of about 20 mK. The amplifiers and filters are used in our measurement circuit to increase the signal-to-noise ratio and isolate the device from external noise.
In our experiment setup, two microwave vector signal generators combined with four digital to analog converter (DAC) channels of an Arbitrary Wave Generator (AWG) of the model Tektronix 5014c is used to irradiate the transmon qutrit on-resonance with the transition frequency ω01 and ω12 respectively. The four DAC channels generate square waveforms of different amplitudes and lengths for IQ (In-phase and Quadrature) mixers on the vector signal generators to realize a different XY rotation of the qutrit. The amplitude corresponding to the driving strength is firstly calibrated by the Rabi oscillation experiments. Another microwave source is used to read out the qubit states by measuring cavity transmission. Here we choose the “high power readout” scheme,[19] which provides sufficient noise-to-signal ratio of our data and simplifies our experiment procedures and data analysis. Figure
Initially, we prepared the qutrit on the ground state |0⟩. The QFT is then implemented by a sequence of six selective rotation pulses 
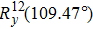
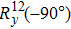

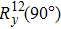
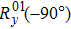

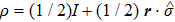
Figure
In this paper, we propose an experimental realization of the quantum permutation algorithm based on a 3D transmon qutrit and demonstrate the implementation of this algorithm to determine the parity of two permutations. The decoherence and the calibration imperfection are the main limits to the fidelity of our experiment, while the fidelity we obtained is still high enough to determine the parity of the permutations. Employing the third state of the transmon realizes the single step query speed-up in this experiment, which shows the potential power of a multi-level system in processing quantum information. This experiment also provides a possible way for theoretical discussion and exploring the origin of quantum speed-up.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] |