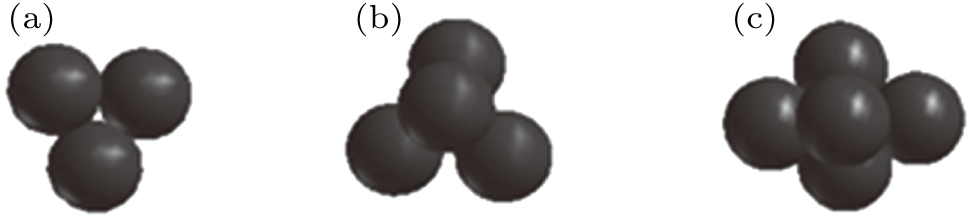Cite this Article
Zhang Bao-Ling, Wang Bao-Wen, Su Xue, Song Xiao-Yong, Li Min. Growth mode of helium crystal near dislocations in titanium*

Project supported by the National Natural Science Foundation of China (Grant No. 11505120) and the Project of Innovative Talents of North China University of Water Resources and Electric Power, China (Grant No. 70483).

 . Chinese Physics B, 2018, 27(6): 060205  
Permissions
Growth mode of helium crystal near dislocations in titanium*

Project supported by the National Natural Science Foundation of China (Grant No. 11505120) and the Project of Innovative Talents of North China University of Water Resources and Electric Power, China (Grant No. 70483).
Zhang Bao-Ling1, 2, †, Wang Bao-Wen1, Su Xue1, Song Xiao-Yong1, Li Min2
North China University of Water Resources and Electric Power, Zhengzhou 450011, China
Institute of Nuclear Science and Technology, Sichuan University, Chengdu 610064, China

 

† Corresponding author. E-mail: zbaoling1234@163.com

Project supported by the National Natural Science Foundation of China (Grant No. 11505120) and the Project of Innovative Talents of North China University of Water Resources and Electric Power, China (Grant No. 70483).

Abstract

The helium bubble structure and growth modes near dislocations in titanium are studied using the molecular dynamics method. A helium crystal with an HCP structure in titanium is found to have a lattice constant of 1.977 Å at 0 K. On either side of the slip plane, helium bubbles form in the (001) plane, but they are in different growth modes. On the side of the slip plane with full atomic layers, helium bubbles grow toward the slip plane and easily cross the slip plane. In the growth process, the position of the top surface of the helium bubble remains almost unchanged. On the other side of the slip plane, the helium bubble grows initially toward the dislocation core, but it is difficult to cross the slip plane, which results in growth in the opposite direction upon reaching the slip plane.

PACS: 02.70.Ns;28.52.Fa
Keyword:molecular dynamics;helium bubble structure;titanium
1. Introduction

Helium atoms are usually introduced into metals through ion implantation, tritium decay, or (n, α) reactions during neutron irradiation.[1–3] It is difficult to dissolve helium atoms in metals, because they easily migrate and accumulate, forming helium bubbles. The pressures inside the bubbles are very large, which can destroy the mechanical properties of the materials.[4–8] The changes in the mechanical properties of the materials reduce the safety of nuclear installations and shorten their service life, thus it becomes important to study the behaviors of helium atoms in metals.

So far, a considerable amount of research has focused on the experimental and theoretical aspects of helium in iron and tungsten,[9–14] while only a few studies have been devoted to the behaviors of helium atoms in titanium, which is often used as a structural material in nuclear power plants. In a fast neutron reactor, titanium is a competitive candidate as a cladding material. In addition, titanium has the ability to absorb hydrogen, providing a useful tritium storage material.[15]

In previous studies, the behavior of helium in perfect titanium crystal was simulated,[16,17] and some useful results were obtained. In this study, we analyze the structures and growth modes of helium bubbles near dislocations in titanium using the molecular dynamics (MD) method. Different growth modes and HCP crystal structures of helium bubbles near the dislocations in titanium are observed, thus providing further insight into the behavior of helium in titanium.

2. Simulation method

An MD box (24a0 × 24b0 × 22c0) is used to simulate the growth of a helium bubble near a dislocation in bulk titanium, where a0, b0, and c0 are the lattice constants of titanium. Periodic boundary conditions are applied to the direction of the Boggs vector and also to the direction of the dislocation. The interaction between the Ti–Ti atoms is described by the interatomic potentials of Fabrizio et al.[18] The He–He interaction is described by the well-known Lennard–Jones potential.[19] The Ti–He potential is constructed by fitting the pair potential to ab initio data.[17] This set of potentials has been used in our recent studies, providing a good description of the bulk properties and defect properties of the Ti–He system.[16,17]

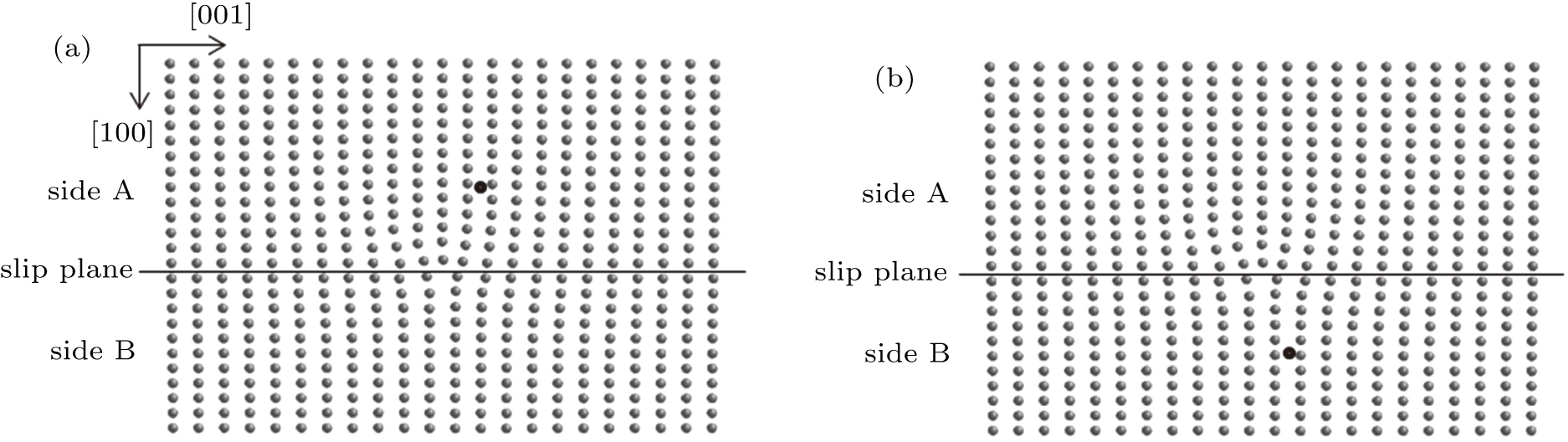
The periodic atomic arrays of dislocations are constructed based on the method proposed by Daw and Baskes, which has proved to be very successful in studying edge dislocation.[20–22] The titanium crystal is divided into two parts along the slip plane. One part is made of N atomic layers, and the other part is composed of N – 1 atomic layers, with the total width of the two parts being the same so that the interface of the two parts has a specific dislocation. The system is relaxed at 0 K to attain the lowest energy state, and a titanium substrate containing edge dislocation is formed. For convenience, the side of the substrate containing N atomic layers is named side A, and the other side containing N – 1 atomic layers is called side B.

In the following simulations, the first helium atom is placed at an interstitial site on sides A and B as shown in Figs. 1(a) and 1(b), respectively. For each system, the second helium atom is introduced one lattice distance away from the first helium atom so that they would interact in a short time. Once the system evolves for 50 ps, a new helium atom is added one lattice distance away from the closest helium atom in the helium cluster. The behaviors of helium atoms on sides A and B are observed and compared with each other in detail. The simulation temperature is set to be 0 K to obtain the minimum energy state of the helium bubble, which assists in analyzing the bubble structure.

Fig. 1. First helium atom on each of (a) side A and (b) side B of the slip plane. Grey sphere: Ti atom; Black sphere: He atom.
3. Results and discussion
3.1. Helium bubble growth

On side A of the slip plane, the positions of the helium bubble are shown in Fig. 2, when the bubble contains 20, 60, 100, and 211 helium atoms (see Figs. 2(a)–2(d) respectively). It can be seen that the helium bubble grows downward continuously, while the top surface position remains almost unchanged. At the beginning of the helium bubble growth, the lower surface of the bubble is closer to the slip plane. After the lower surface crosses the slip plane, it moves farther away from the slip plane due to the bubble growth along the [100] direction. The helium bubble forms in the (001) plane, and it is flat in the [001] direction, extending to a thickness of only two atomic layers. In the growth process of the helium bubble, defects are preferentially produced on the side toward where the bubble grows, and drift toward side B. However, the substrate on the other side of the helium bubble almost keeps a perfect crystal structure as shown in Fig. 3.

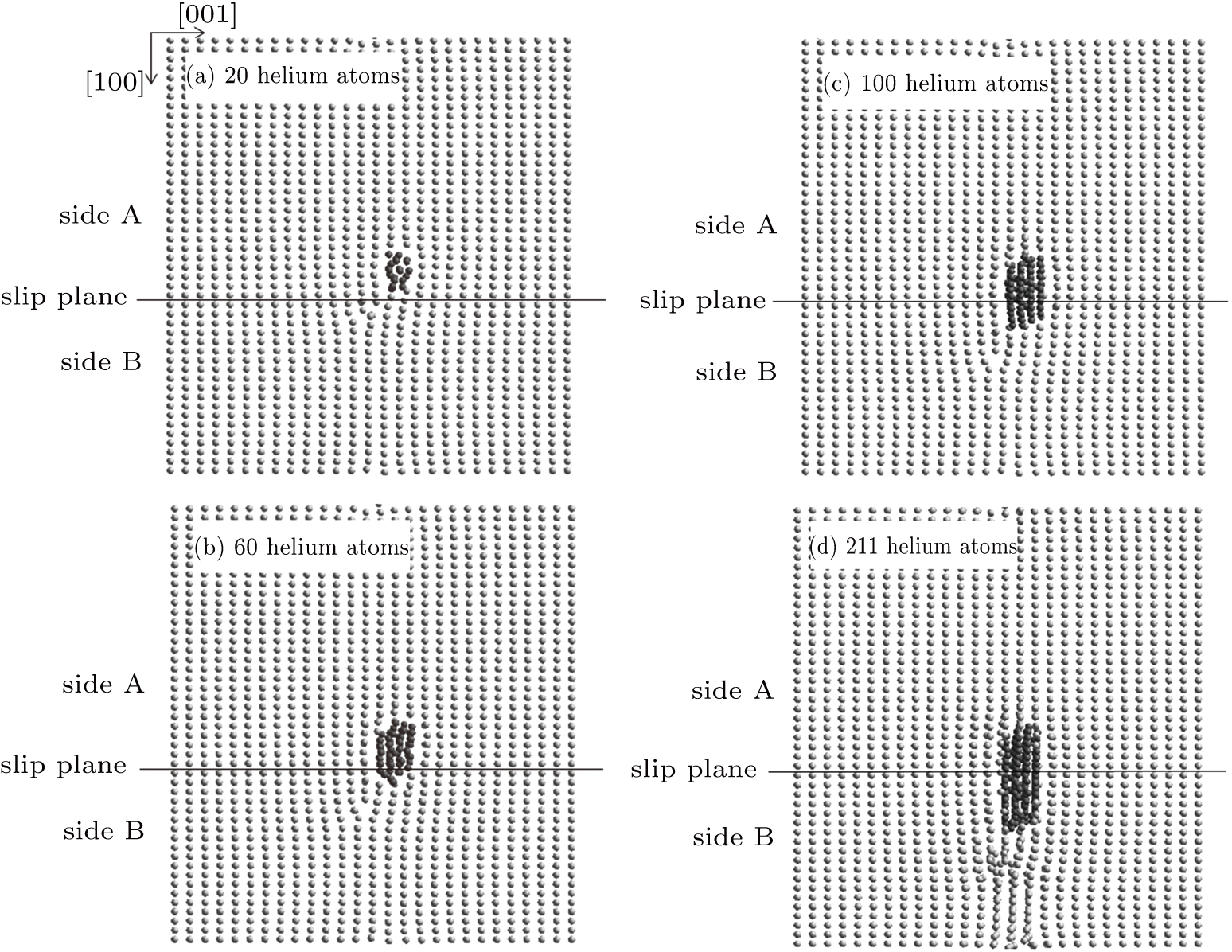Fig. 2. Growth of the helium bubble nucleated on side A of the slip plane in the cases of (a) 20, (b) 60, (c) 100, and (d) 211 helium atoms.
Fig. 3. Defects induced by the helium bubble growth nucleated on side A.

Figure 4 shows the growth process of the helium bubble on side B of the slip plane. Initially, the helium bubble grows toward the dislocation core until it reaches the slip plane, corresponding to the number of helium atoms ranging from 1 to 24. However, it is difficult for the bubble to cross the slip surface, since the other side of the slip plane has a full atomic layer, thereby causing the helium bubble to grow downward along the [100] direction till the end of the simulation, where the number of helium atoms reaches 160. In addition, the helium bubble forms in the (001) plane, extending to a thickness of only two atomic layers in the [001] direction. During the helium bubble growing toward the slip plane, defects are mainly produced in the vicinity of the dislocation core as shown in Fig. 5(a). When the helium bubble grows toward the opposite direction, defects are mainly produced around the helium bubble except on the upper side. That is to say, the one side of the substrate with full atomic layer still has almost no defects as shown in Fig. 5(b).

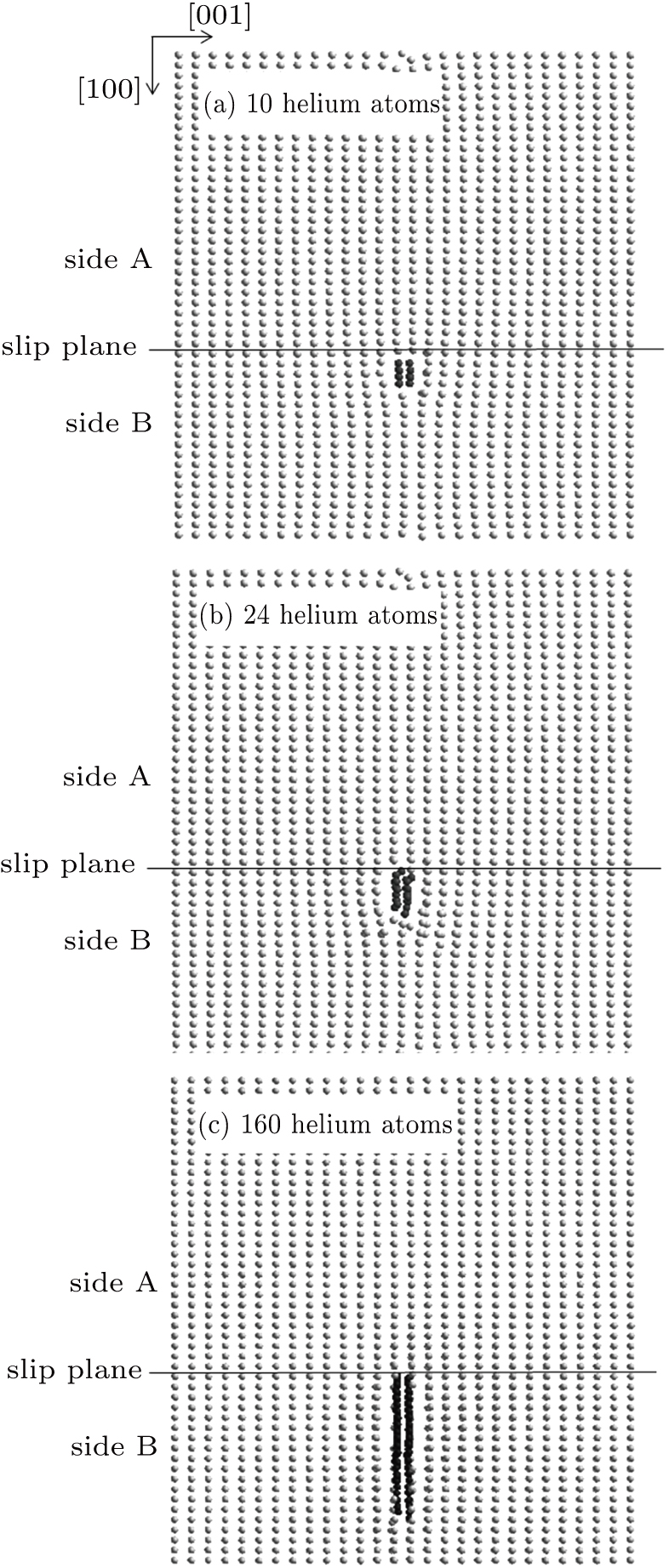Fig. 4. Growth of the helium bubble nucleated on side B of the slip plane, in the cases of (a) 10, (b) 24, and (c) 160 helium atoms.
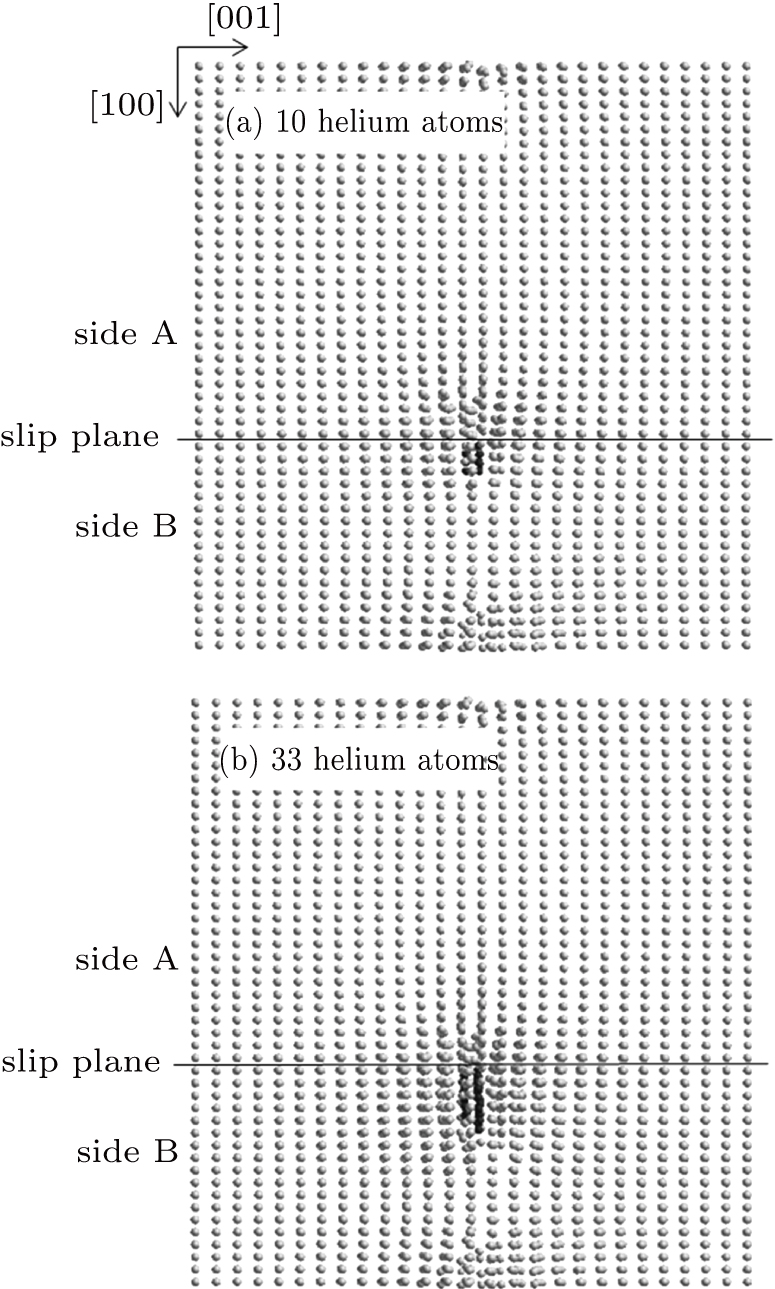Fig. 5. Defects induced by the helium bubble growth nucleated on side B in the cases of (a) 10 and (b) 33 helium atoms.

Then the size of substrate is changed and relaxed at 0 K. The above simulations are repeated and the same phenomena are observed.

3.2. Helium bubble structure

The helium bubbles have the same structure on both sides of the slip plane, except those with different growth modes. Figure 6 shows the cluster structures for the numbers of helium atoms of 3, 4, and 5, respectively. An equilateral triangular structure is formed by three helium atoms, and a regular tetrahedron structure is constituted with four helium atoms. With the addition of more helium atoms, a helium bubble with a regular hexagonal structure forms and grows in the (001) plane. Figure 7 shows 14 helium atoms arranged on side A and 10 helium atoms on side B of the slip plane. Figure 8 shows 211 helium atoms arranged on side A and 160 helium atoms on side B of the slip plane, with helium atoms arranging orderly on either side of the slip plane. Note that ordering appears easier for the helium atoms within the bubble nucleated on side B of the slip plane, since there are vacancies on side B, allowing the helium atoms to move slightly.

Fig. 6. Structures of cluster containing (a) 3, (b) 4, and (c) 5 helium atoms, respectively.
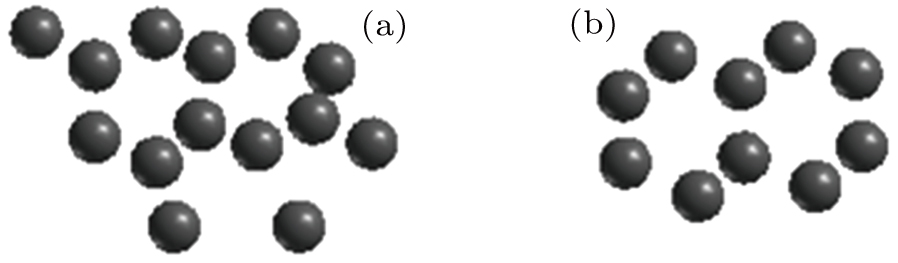Fig. 7. Arrangements of (a) 14 helium atoms on side A and (b)10 helium atoms on side B of the slip plane.
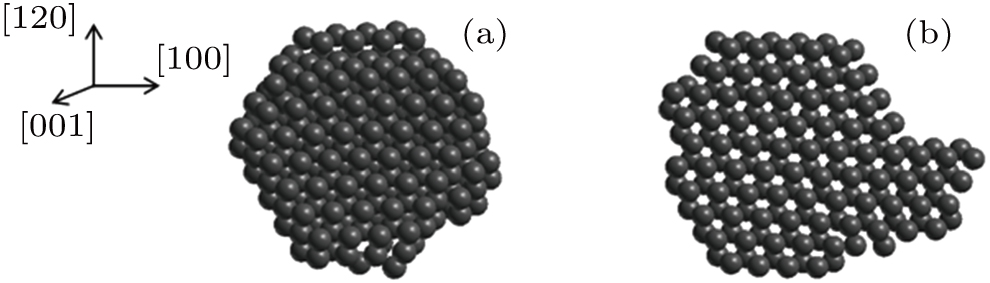Fig. 8. Arrangements of (a) 211 helium atoms within the bubble nucleated on side A and (b) 160 helium atoms within the bubble nucleated on side B of the slip plane.

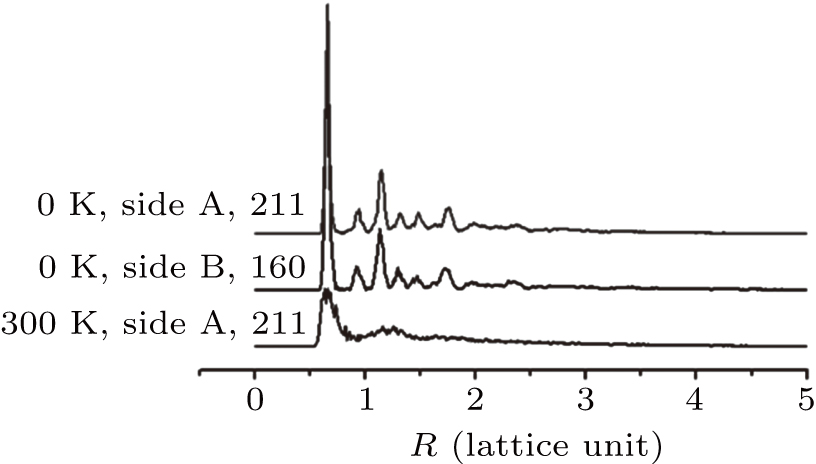
The pair correlation function is used to analyze the arrangement of the helium atoms as shown in Fig. 9. The pair correlation functions of helium atoms have significant crystal characteristics that indicate the formation of a helium crystal. The analysis reveals that the two helium bubbles have the same HCP structure as the substrate, but with a smaller lattice constant. The lattice constant for titanium is a0 = 2.951 Å, while the lattice constant of the helium bubbles is only 0.67a0, ≈ 1.977 Å.

Fig. 9. Pair correlation functions of helium atoms at 0 K and 300 K.

The helium crystal in titanium has been speculated previously in our study on the phase transition of high-density helium.[23] Here, the helium crystal with an HCP structure near the dislocation in titanium is clearly observed. Maji et al.’s study on solid helium bubbles in aluminum analyzed the bubbles using positron lifetime measurements.[24] The lifetime of the positron changed suddenly when the temperature decreased to 190 K, suggesting a change in the helium bubbles from a liquid to a solid state caused by the redistribution of electron density.

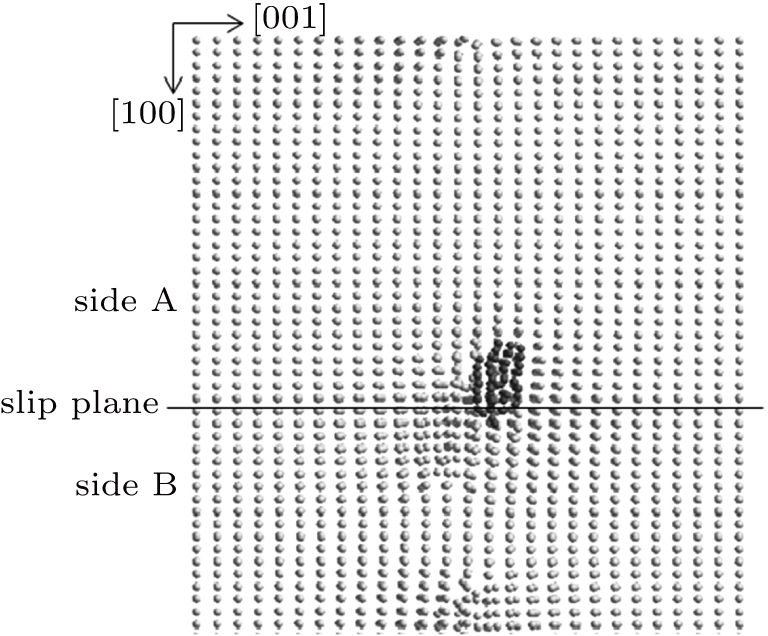
Next, the Ti–He system containing the helium bubble nucleated on side A is increased to 300 K by electron-phonon coupling. In the electron–phonon coupling model, atoms exchange energy with the electron gas in the substrate according to electron–phonon interaction dynamics.[14,25] Due to the high thermal conductivity of the electron gas in metal, the energy transferred to the electron gas is quickly dispersed, and the electron gas is considered to maintain a constant temperature. At 300 K, the helium bubble continuously expands along the [100] direction in the (001) plane as shown in Fig. 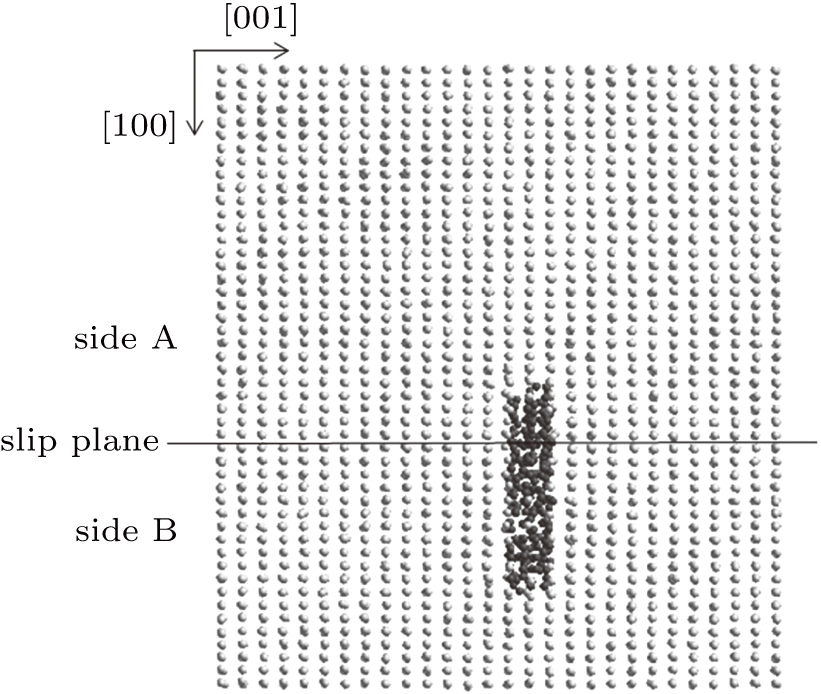10. However, the bubble is still flat in the [001] direction and the thickness is unchanged. Furthermore, the shape of the bubble is distorted in the (001) plane, causing the arrangement of the helium atoms to become disordered as shown in Fig. 11. The pair correlation functions of the helium atoms within the bubble at 300 K are also computed as seen in Fig. 9, where the pair correlation function presents liquid characteristics at 300 K, indicating that the helium bubble is liquid in titanium at room temperature.

Fig. 10. Expansion of the helium bubble nucleated on side A of the slip plane along [100] direction at 300 K.
Fig. 11. Arrangements of 211 helium atoms within the bubble nucleated on side A of the slip plane at 300 K.

In the following simulations, the temperature of the substrate is set to be 300 K. Helium atoms are added near dislocations to make a comparison with the simulation results of 0 K. Similar phenomena are observed as follows. On the side of the slip plane with full atomic layers, a helium bubble grows toward the slip plane and easily crosses the slip plane. On the other side of the slip plane, the helium bubble has difficulty in crossing the slip plane. It grows initially toward the dislocation core and then grows in the opposite direction. However, the arrangements of the helium atoms are disordered, i.e., helium bubbles do not exhibit a crystal structure at 300 K.

4. Conclusions

Helium bubble structure and growth near dislocations in titanium have been analyzed using the molecular dynamics method. A helium bubble is shown to form in the (001) plane on either side of the slip plane, but with different growth modes. On the side of the slip plane with full atomic layers, the helium bubble grows toward the slip plane, and then crosses the slip plane easily. In the growth process, the top surface position of the helium bubble remains almost unchanged. On the other side of the slip plane, the helium bubble grows toward the dislocation core initially, but experiences difficulty in crossing the slip plane, and grows toward the opposite direction after reaching the slip plane. Generally, the helium bubble tends to grow toward the dislocation core, or alternately towards the side of the slip plane that lacks an atomic layer. It is interesting to note that the helium bubble demonstrates an HCP crystal structure with a lattice constant of about 1.977 Å at 0 K near the dislocation in titanium, but it is liquid at 300 K.

Reference
[1] Cottrell G A 2006 Mater. Sci. Technol. 22 869
[2] Dethloff C Gaganidze E Svetukhin V V Aktaa J 2012 J. Nucl. Mater. 426 287
[3] Cheng G J Shi L Q Zhou X S Liang J H Wang W D 2015 J. Nucl. Mater. 466 615
[4] Klimenkov M MÖslang A Materna M E 2014 J. Nucl. Mater. 453 54
[5] Chen J Jung P Rebac T Duvalb F Sauvageb T Carlanc D Y Bartheb M F 2014 J. Nucl. Mater. 453 253
[6] Sakaguchi N Ohguchi Y Shibayama T Watanabe S Kinoshita H 2013 J. Nucl. Mater. 432 23
[7] Cipiti B B Kulcinski G L 2005 J. Nucl. Mater. 347 298
[8] Bernard E Sakamoto R Yoshidaa N Yamada H 2015 J. Nucl. Mater. 463 316
[9] Stoller R E Osetsky Y N 2014 J. Nucl. Mater. 455 258
[10] Valles G Gonzále C Martin B I glesias R Perlado J M 2015 J. Nucl. Mater. 457 80
[11] Smirnov R D Krasheninnikov S I Guterl J 2015 J. Nucl. Mater. 463 359
[12] Li X C Shu X L Tao P Yi Y B Niu G J Xu Y P Gao F Luo G N 2014 J. Nucl. Mater. 455 544
[13] Zhang L Fu C C Lv G H 2013 Phys. Rev. B 87 134107
[14] Li M Wang J Hou Q. 2012 J. Nucl. Mater. 423 22
[15] Zhou X S Liu Q Zhang L Peng S M Long X G Ding W Cheng G J Wang W D Liang J H Fu Y Q 2014 Int. J. Hydrogen Energy 39 20062
[16] Zhang B L Wang J Li M 2013 J. Nucl. Mater. 438 178
[17] Wang J Hou Q 2007 J. Appl. Phys. 102 093510
[18] Cleri F Rosato V 1993 Phys. Rev. B 48 22
[19] Donnelly S E Evans J H Fundamental Aspects of Inert Gases in Solids New York Plenum Press
[20] Rodney D Martin G 1999 Phys. Rev. Lett. 82 3272
[21] Chang J P Bulatov V V Yip S 1999 J. Computer-aided Materials Design 6 165
[22] Osetsky N Y Bacon D J 2003 Model. Simul. Mater. Sci. Eng. 11 427
[23] Zhang B L Song X Y Hou Q Wang J 2015 Acta Phys. Sin. 64 016202 in Chinese
[24] Maji S Singh A Nambissan P M 2001 Phys. Lett. A 281 76
[25] Hou Q Hou M Bardotti L Prével B Mélinon P Perez A 2000 Phys. Rev. B 62 2825