Project supported by the Wuhan Applied Basic Research Project, China (Grant No. 20140101010009), the National Natural Science Foundation of China (Grant Nos. 61405063, 61475054, 11574105, and 61177095), the Hubei Science and Technology Agency Project, China (Grant No. 2015BCE052), and the Fundamental Research Funds for the Central Universities, China (Grant No. 2017KFYXJJ029).
Project supported by the Wuhan Applied Basic Research Project, China (Grant No. 20140101010009), the National Natural Science Foundation of China (Grant Nos. 61405063, 61475054, 11574105, and 61177095), the Hubei Science and Technology Agency Project, China (Grant No. 2015BCE052), and the Fundamental Research Funds for the Central Universities, China (Grant No. 2017KFYXJJ029).
† Corresponding author. E-mail:
Project supported by the Wuhan Applied Basic Research Project, China (Grant No. 20140101010009), the National Natural Science Foundation of China (Grant Nos. 61405063, 61475054, 11574105, and 61177095), the Hubei Science and Technology Agency Project, China (Grant No. 2015BCE052), and the Fundamental Research Funds for the Central Universities, China (Grant No. 2017KFYXJJ029).
It has been proposed previously that the coherent detection of a terahertz (THz) pulse can be achieved based on the time-resolved luminescence quenching. In this paper, we investigate the frequency response range of this novel detection technology by simulating the motion of carriers in gallium arsenide (GaAs) by the ensemble Monte Carlo method. At room temperature, for a direct-current (DC) voltage of 20 kV/cm applied to the semiconductor (GaAs) and sampling time of 140 fs, the luminescence quenching phenomena induced by terahertz pulses with different center frequencies are studied. The results show that the quenching efficiency is independent of the THz frequency when the frequency is in a range of 0.1 THz–4 THz. However, when the frequency exceeds 4 THz, the efficiency decreases with the increase of frequency. Therefore, the frequency response range is 0.1 THz–4 THz. Moreover, when the sampling time is changed to 100 fs, the frequency response range is extended to be approximately 0.1 THz–5.6 THz. This study of the frequency-dependent characteristics of the luminescence response to the THz pulse can provide a theoretical basis for the exploration of THz detection technology.
A terahertz (THz) wave is an electromagnetic wave with a frequency range from 0.1 THz to 10 THz, which is located between microwave and the far infrared. The wavelength, wave number, and energy of a 1-THz photon are 300 μm, 33.3 cm−1, and 4.14 meV,[1,2] respectively. The continuous progress of THz technology has led to the gradual expansion of its applications, making the detection of terahertz pulses a key issue. THz detection technology can be divided into two types: incoherent detection and coherent detection. For example, Bolometers, pyroelectric detectors and Golay cells are incoherent detection techniques, which are used to detect the radiation of terahertz wave.[3] Electro-optic (EO) sampling,[3] antenna detection,[4,5] and heterodyne detector[3] are coherent detection techniques, and they have the ability to detect the electric field of THz pulse. In practical applications, the detection technology can be selected according to the specific circumstances. In order to enhance the performance and functionalities of the detectors for various applications, a novel theoretical THz pulse detection method was proposed in a previous study.[6]
The electron transport caused by a THz pulse has aroused significant interest,[6–10] which is the basis of the new detection theory. In our earlier work, it has already been suggested that the coherent detection of THz pulses can be realized based on the THzinduced time-resolved luminescence quenching,[6] because the changes in the luminescence and THz pulse waveforms are reversed when the THz pulse irradiates the semiconductor under a direct-current (DC) voltage at room temperature. In this paper, we theoretically investigate the frequency response range of this new detection method. The time-domain spectra and frequency spectra of luminescence for terahertz pulses with different center frequencies are obtained by using the ensemble Monte Carlo method, which are then compared with the corresponding time-domain spectra and frequency spectra of the incident terahertz pulses. This comparison enables the study of the frequency-dependent characteristics of the luminescence response to the THz pulse. This paper improves the theoretical approach to the new detection technology, thus guiding future experiments.
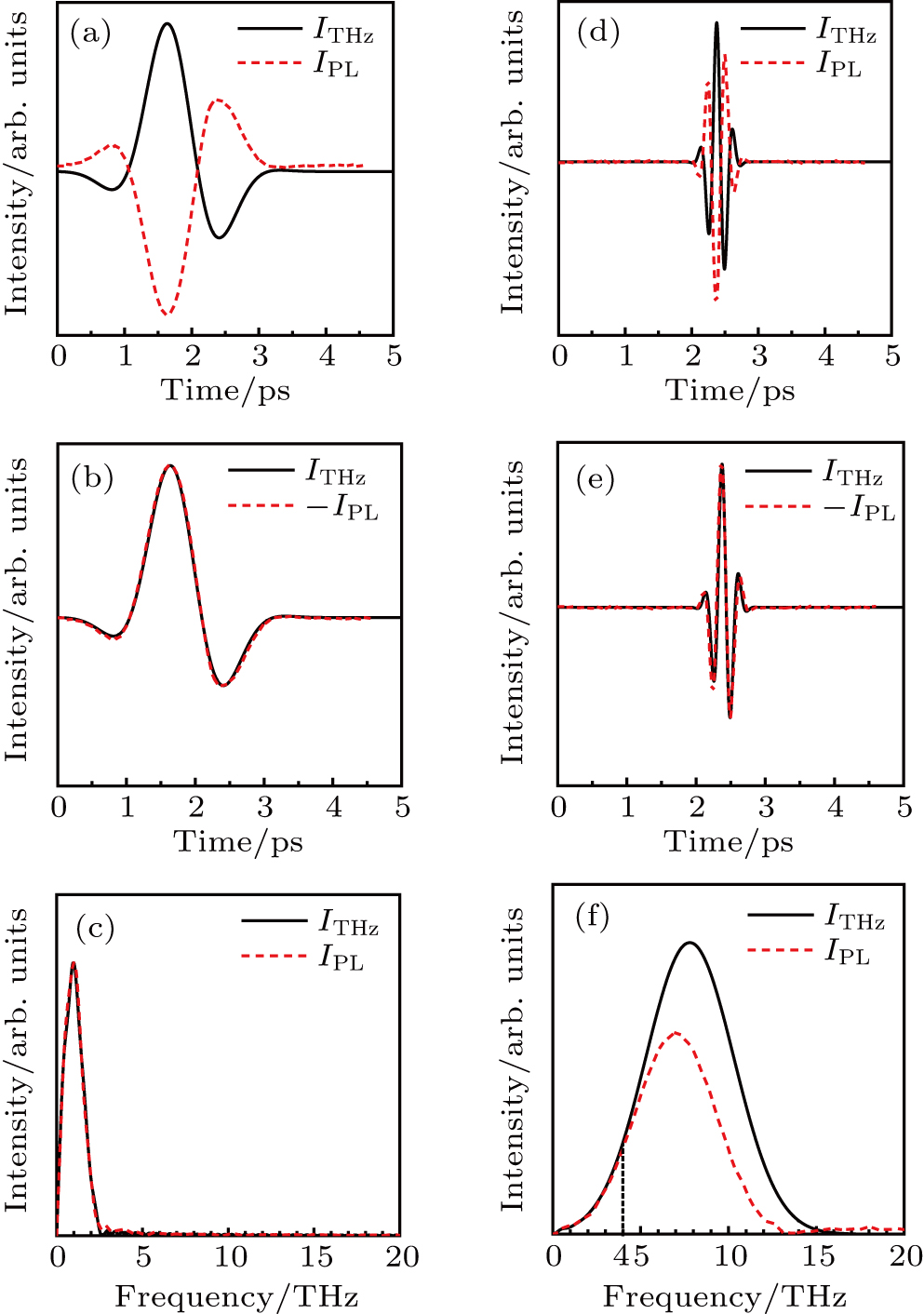
As shown in Fig.
To investigate the distributions of the electrons in the three valleys corresponding to different incident THz pulses, the Boltzmann equation is used to describe the motion of electrons in the THz field, which is studied by the ensemble Monte Carlo method[9,10,15–23]
 |

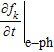
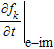

The electron distribution fk can be obtained by solving Eq. (
The center wavelength of the excitation laser is 800 nm, whose photon energy is 1.54 eV, which is slightly higher than the band gap of GaAs (1.45 eV). Therefore, the energy of the excited electrons is about 0.09 eV when they arrive at the bottom of the Γ valley, which is much lower than the ΔEΓ–L. The room temperature is 300 K, and the threshold voltage of the luminescence quenching response to an external electric field is 20 kV/cm.[6] The sampling time should be in a range of 100 fs–200 fs,[6] because the quenching phenomenon is unobvious when the sampling time is too short, whereas it can easily appear as nonlinearity when the sampling time is too large. In this simulation, the DC field is set to be 20 kV/cm, while the sampling time is set to be 140 fs. Under these conditions, the electrons in the Γ valley can just be driven to the L valley, but not to the X valley. Simultaneously, the weak part of the THz pulse can also trigger responses.
The luminescence quenching efficiency is calculated from
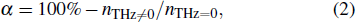 |
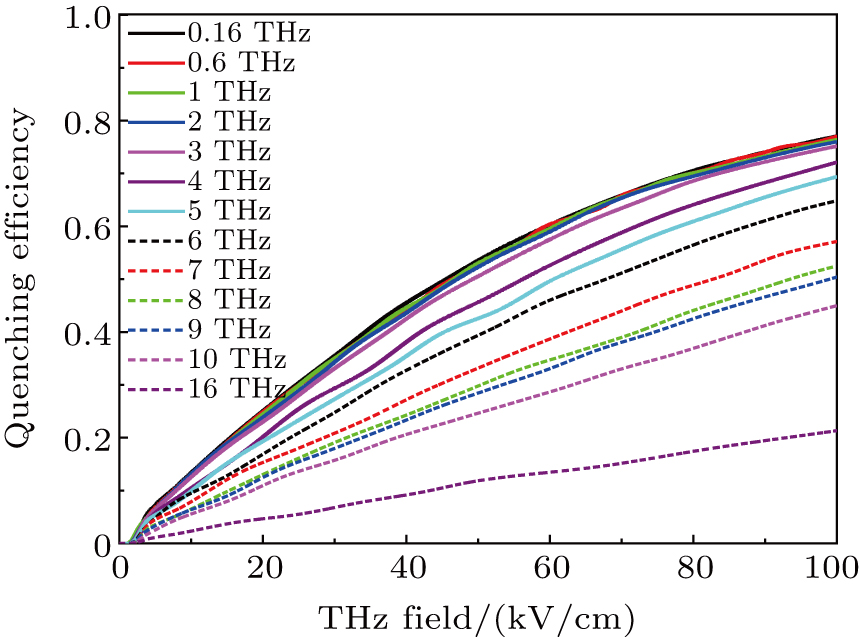
The quenching efficiency curves corresponding to 0.16, 0.6, 1, 2, and 3 THz almost coincide with each other, which implies that the quenching efficiency is independent of the frequency in the low-frequency region. In comparison, the curves corresponding to 4, 5, 6, 7, 8, 9, 10 THz, and 16 THz show that the quenching efficiency decreases with the increase of the frequency.
The ITHz and IPL denote the intensities of the THz pulse and luminescence, respectively. The luminescence intensity can be expressed as a sum of two terms:
 |
Figures
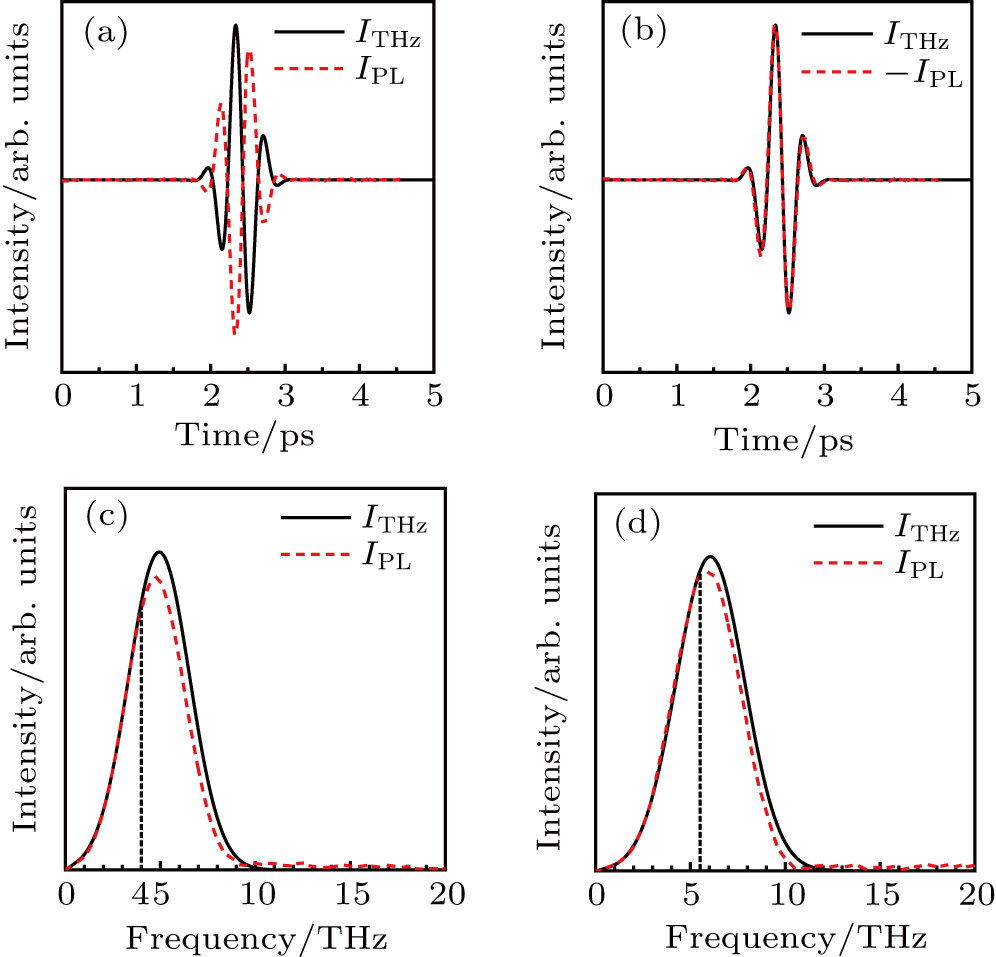
To verify the above results, figure
Based on those analyses, it is proposed that the frequency response range be approximately 0.1 THz–4 THz, when the DC field is 20 kV/cm and sampling time is 140 fs. In this case, the quenching efficiency of luminescence induced by the THz pulse is independent of frequency. However, when the frequency is higher than 4 THz, the efficiency decreases with the increase of frequency.
The optical power P can be calculated from
 |
 |
According to the above analysis, t is another important parameter that can affect the quenching efficiency. For further investigation, the sampling time is changed to 100 fs, and the center frequency of THz pulse is 6 THz. Figure
In this paper, we have theoretically studied the frequency characteristics of a THz-induced time-resolved luminescence quenching in GaAs based on the ensemble Monte Carlo method to obtain the frequency response range of the THz-pulse coherent detection method. For a DC field of 20 kV/cm applied to the semiconductor (GaAs) and sampling time of 140 fs, at room temperature (300 K), the luminescence quenching induced by THz pulses with different center frequencies is studied. The results show that from 0.1 THz to approximately 4 THz, the quenching efficiency is independent of frequency, whereas from 4 THz to 10 THz, the quenching efficiency decreases with the increase of frequency. That means that in a frequency range of 0.1 THz–4 THz, the spectra of luminescence and the incident THz pulse are coincident, whereas in the higher frequency region, the spectra of luminescence and the incident THz pulse are not coincident. When the sampling time is reduced to 100 fs, this range is expanded to 0.1 THz–5.6 THz. Therefore, it can be concluded that for a DC field of 20 kV/cm and sampling time of 140 fs, the frequency response range of the THz-pulse coherent detection based on semiconductor (GaAs) time-resolved luminescence quenching is approximately 0.1 THz–4 THz, and that the range could be expanded by reducing the sampling time. This paper provides a theoretical basis for the new terahertz coherent detection technology, which will be helpful in the future research.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] |