Project supported by the National Basic Research Program of China (Grant No. 2013CB922204), the National Natural Science Foundation of China (Grant Nos. 11574115 and 11704146), and the Natural Science Foundation of Jilin Province, China (Grant No. 20150101063JC).
Project supported by the National Basic Research Program of China (Grant No. 2013CB922204), the National Natural Science Foundation of China (Grant Nos. 11574115 and 11704146), and the Natural Science Foundation of Jilin Province, China (Grant No. 20150101063JC).
† Corresponding author. E-mail:
Project supported by the National Basic Research Program of China (Grant No. 2013CB922204), the National Natural Science Foundation of China (Grant Nos. 11574115 and 11704146), and the Natural Science Foundation of Jilin Province, China (Grant No. 20150101063JC).
Time-dependent density functional theory (TDDFT) method is used to investigate the details of the excited state intramolecular proton transfer (ESIPT) process and the mechanism for temperature effect on the Enol*/Keto* emission ratio for the Me2N-substited flavonoid (MNF) compound. The geometric structures of the S0 and S1 states are denoted as the Enol, Enol*, and Keto*. In addition, the absorption and fluorescence peaks are also calculated. It is noted that the calculated large Stokes shift is in good agreement with the experimental result. Furthermore, our results confirm that the ESIPT process happens upon photoexcitation, which is distinctly monitored by the formation and disappearance of the characteristic peaks of infrared (IR) spectra involved in the proton transfer and in the potential energy curves. Besides, the calculations of highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) reveal that the electronegativity change of proton acceptor due to the intramolecular charge redistribution in the S1 state induces the ESIPT. Moreover, the thermodynamic calculation for the MNF shows that the Enol*/Keto* emission ratio decreasing with temperature increasing arises from the barrier lowering of ESIPT.
Excited-state intramolecular proton transfer (ESIPT), discovered first by Weller,[1] is still the subject of experimental and theoretical investigation.[2–12] Compounds that undergo ESIPT have attracted attention due to their applications in fluorescent probes,[13–15] bioimaging,[16] light-emitting materials,[17] photostabilizers,[18] and photophysical studies.[19,20] The most common spectral features of a molecule undergoing ESIPT are interesting dual fluorescence and large Stokes shift.[21]
Recently, a number of functional organic molecules based on ESIPT which exhibit dual fluorescence have been investigated extensively.[22,23] It is well known that the molecules exhibit the ESIPT properties involving a heterocyclic ring which is formed by the intramolecular hydrogen bond between a hydroxyl group and a neighboring proton acceptor.[21,24–26] Generally, ESIPT fluorophores show dual emission bands creating normal emission from Enol* form (high energy) and ESIPT emission from Keto* form (low energy).[22,27,28] It suggests that the tautomerism produces dual fluorescence and the structural geometry of the Keto emissive excited-state is significantly displaced from that of the ground state.[17,20,29]
Attention is particularly paid to the flavonoid compounds which can serve as the probe to investigate the ESIPT process and also may reveal the relationship between ESIPT and luminescence property.[30] As an important natural pigment, flavonoids constitute a major portion of natural products present in fruits and vegetables,[31,32] and are responsible for the colors in fruits and vegetables.[33] The flavonoids can be used as chemical sensors and DNA recognition due to low toxicity and attractive properties of selective binding to proteins.[34,35] The presence of hydroxyl group and proton acceptor in the flavonoids allows the molecule to undergo the ESIPT process, which means that the Keto* state is corresponding to the ESIPT emission. Meanwhile, another notable feature in the flavonoid relating to the potential intramolecular charge transfer (ICT), i.e., the Enol* state is corresponding to the ICT emission. It should be noted that the ICT is not only coexistent with ESIPT, but also across the path of ESIPT in flavonoid.[30] Respectively, the two photo-induced processes (ICT and ESIPT) have been extensively studied, however little is known about their relative importance.
Recently, Bi et al. used the experimental method of changing temperature to control the relative strength ratio between ICT emission and ESIPT emission for the Me2N-substitued flavonoid (MNF) compound.[30] They found that the Keto* form (ESIPT state) emission gradually becomes stronger and the Enol* form (ICT state) emission turns weaker as the temperature rises from −80 °C to room temperature. However, the mechanism for temperature effect on the luminescence properties for MNF remains unknown. A rational sensor design is dependent on the fundamental understanding of the interaction between ICT and ESIPT under different temperatures that control the sensor performance.
In the present work, we investigate the MNF molecule theoretically, aiming at exploring the details of ESIPT process for the MNF molecule and explaining the temperature effect on the Enol*/Keto* emission ratio. Especially, the structures of MNF in S0 state and the S1 state are optimized through the DFT and TDDFT methods, respectively. In addition, the very important information about its absorption peak and fluorescence peaks is also obtained. The differences in IR spectrum among different states are circumstantiated. Simultaneously, the potential energy curves along the proton transfer coordinate both in the ground and in the excited state are investigated as well. Moreover, we perform the thermodynamic calculation for the MNF to discover the mechanism for temperature effect on the Enol*/Keto* emission ratio, which is helpful to improve the performance of sensor based on MNF material.
In the present work, the ground-state and electronic excited-state geometry were optimized by the DFT and TDDFT[36–43] methods respectively. The Becke’s three-parameter hybrid exchange function with Lee–Yang–Parr gradient-corrected correlation (B3LYP)[44,45] functional and the triple-ζ valence quality with one set of polarization functions (TZVP)[46] basis set were used in our DFT and TDDFT calculation. Moreover, no constrains for symmetry, bonds, angles, or dihedral angles were employed in the geometry optimization calculations. As for the solvent effect, dichloromethane was used as solvent in the self-consistent reaction field (SCRF) calculations through the polarizable continuum model using the integral equation formalism variant (IEFPCM).[47–49] The electronic structure was calculated using the Gaussian 09 program suite.[50] Moreover, the further processing of data is executed using the Multiwfn 3.3.9 program suite.[51]
Table
| Table 1. Calculated absorption peak and emission peak of MNF molecule and experimental data. . |
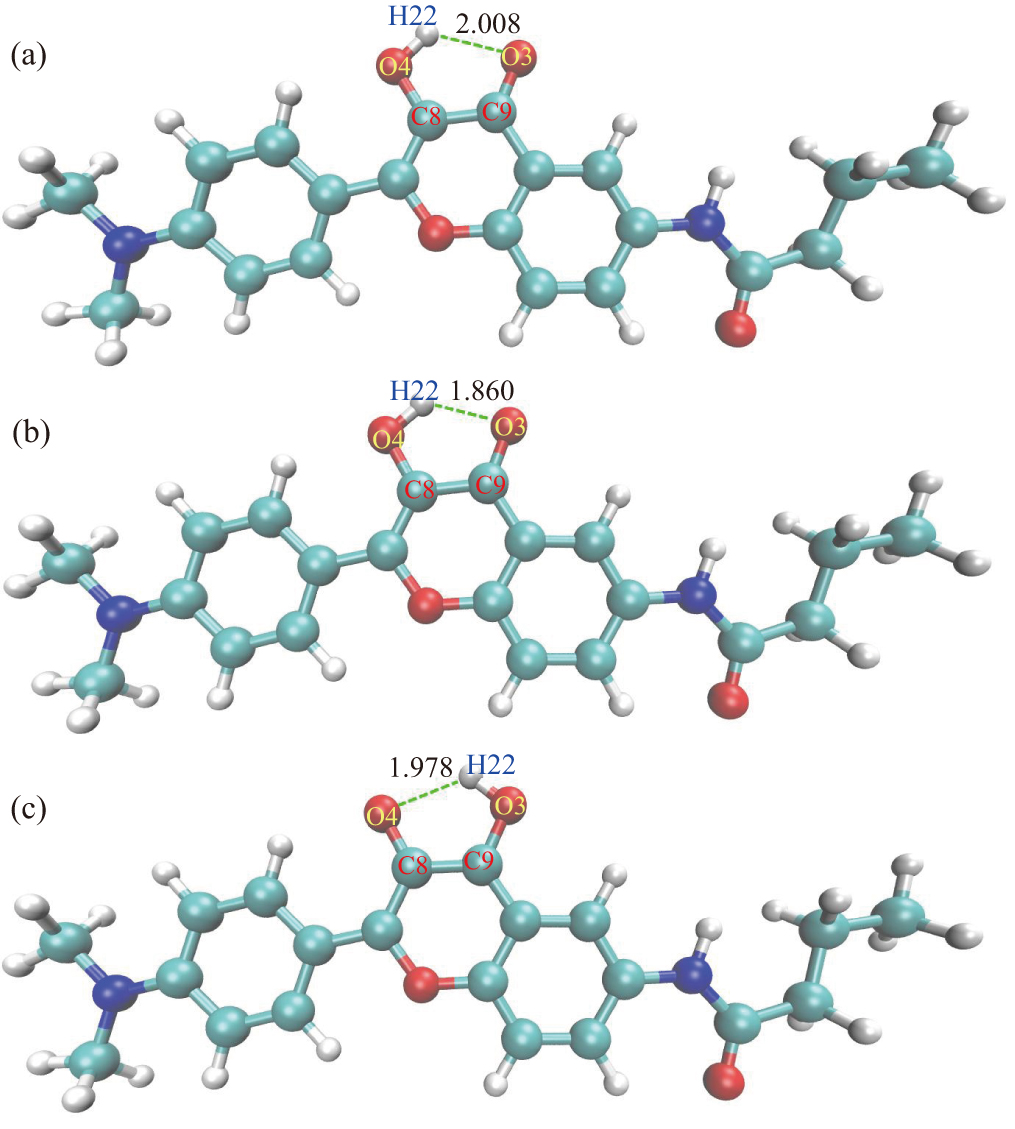
To depict the mechanism for de-excitation for MNF, we optimize the geometric conformations of the Enol (S0), Enol* (S1), and Keto* (S1) forms shown in Fig.
| Table 2. Calculated bond lengths (Å) and bond angles (deg) of the MNF molecule in different electronic states. . |
To investigate the nature of the excited state for the MNF, the frontier molecular orbitals are analyzed. Through the absorption peak calculation, we demonstrate that the S1 state of the MNF corresponds to the highest occupied molecular orbital (HOMO) → lowest unoccupied molecular orbital (LUMO) transition. In Fig.
The other aspect relevant to the ESIPT process is the IR spectra. The vibrational frequencies of the stretching vibrations of O–H group that are involved in hydrogen bonds, as is well known, can provide a distinct signature of the ESIPT.[9] In the present work, we calculate the IR spectra (scale factor 0.9630[52]) of MNF at the S0 and S1 states (Enol* and Keto* forms). The calculated IR spectra of the ground state and S1 state in a spectral range from 2800 to 3600 cm−1 are shown in Fig.
To demonstrate the details of the ESIPT process and explore the mechanism for de-excitation for the MNF upon excitation to the S1 state, we calculate the potential energy curves in different electronic states. The potential energy curves are optimized by fixing the spacing between O4 and H22 (proton transfer coordinate) at different values, which are recorded in Fig.
In the experimental investigation of Bi,[30] the fluorescence intensity ratio of FICT/FESIPT for the MNF decreases with temperature increasing (−80°C–25°C). To find the reason why this interesting phenomenon happens, we calculate the sum of electronic and thermal free energies of transition state in the ESIPT process for the MNF at different temperatures. Figure
The TDDFT method has been used to investigate the details of the ESIPT process and discover the mechanism for the temperature effect on the Enol*/Keto* emission ratio for the MNF. The calculation of geometric structures reveals that the interaction between O3 and H22 increases upon excitation due to the shorter IMHB, and subsequently the H22 transfers from O4 to O3. The vibrational absorption spectra of the hydroxyl group in ground state and the first electronically excited-state are also calculated. The formation and disappearance of the characteristic peaks involved in the formation of hydrogen bonds in different states correlate well with the results that the H22 transfers from O4 to O3, which confirms the ESIPT process for the MNF. Through the calculation of HOMO and LUMO, we demonstrate that the electronegativity change of O3 due to the intramolecular charge redistribution in the S1 state induces the ESIPT. Meanwhile, the Enol* form is attributed to the ICT state. In addition, the results of calculated potential energy curves are the direct evidence for the ESIPT (Enol*→Keto*) and explain the dual fluorescence spectral feature. Furthermore, we perform the thermodynamic calculation for the MNF to discover the mechanism for temperature effect on the Enol*/Keto* emission ratio. We attribute the interesting phenomenon to barrier lowering of ESIPT process induced by increasing temperature. It is hoped that the result is helpful in improving the performance of sensor based on MNF material.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] |