Project supported by the National Natural Science Foundation of China (Grant No. 21373131), the Provincial Natural Science Foundation of Shanxi, China (Grant No. 2015011004), and the Research Foundation for Excellent Talents of Shanxi Provincial Department of Human Resources and Social Security, China.
Project supported by the National Natural Science Foundation of China (Grant No. 21373131), the Provincial Natural Science Foundation of Shanxi, China (Grant No. 2015011004), and the Research Foundation for Excellent Talents of Shanxi Provincial Department of Human Resources and Social Security, China.
† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 21373131), the Provincial Natural Science Foundation of Shanxi, China (Grant No. 2015011004), and the Research Foundation for Excellent Talents of Shanxi Provincial Department of Human Resources and Social Security, China.
We investigated phase transitions in a diblock copolymer–homopolymer hybrid system blended with nanorods (NRs) by using the time-dependent Ginzburg–Landau theory. We systematically studied the effects of the number, length and infiltration properties of the NRs on the self-assembly of the composites and the phase transitions occurring in the material. An analysis of the phase diagram was carried out to obtain the formation conditions of sea island structure nanorodbased aggregate, sea island structure nanorod-based dispersion, lamellar structure nanorod-based multilayer arrangement and nanowire structure. Further analysis of the evolution of the domain sizes and the distribution of the nanorod angle microphase structure was performed. Our simulation provides theoretical guidance for the preparation of ordered nanowire structures and a reference to improve the function of a polymer nanocomposite material.
Polymer nanocomposites play a significant technological role in functional materials because of their excellent performance in optical and electronic devices.[1–8] The most promising research subject in polymer nanocomposites is the preparation of highly ordered and controllable nanostructures.[9–11] However, controlling morphology with minimal effort in materials processing remains a considerable challenge. Since the morphology of polymer blends is one of the factors that determines their properties, studying its control is a significant subject in polymer nanocomposite research. For many practical applications, the addition of nanoparticles has been considered as an effective route to material improvement and an important method for creating highly ordered structures.[12–16] In particular, the addition of anisotropic nanoparticles (such as nanorods) to polymeric materials can be beneficial and increase their photoelectric characteristics, optical properties and mechanical properties.[17–23] The nanorods of noble metals (such as gold) and semiconductors (such as CdSe) possess interesting photoelectrical properties and can significantly improve the efficiency of polymer photovoltaic devices by enhancing their carrier mobilities.[24]
In addition, the alignment of nanorods and nanowires plays an important role in determining the electrical conductivity of polymer nanocomposites.[25–28] Therefore, studying how the self-assembly of nanorods into ordered arrays can be facilitated is an important area in nanotechnology. In an early theoretical study, Balazs et al. used a coarse-grained model for simulating the self-assembly of binary nanorods.[29] The results showed that when the nanorods have an affinity for one polymer, a component can seed the formation of needle-like percolating networks. Ma et al. studied the self-assembly of nanorods in a binary mixture[30] and a diblock copolymer[31] by using a computer simulation method. Their works discussed the influence of the rod–rod interaction, the wetting strength and the rod number density on the architecture and obtained a highly ordered structure of nanowires. Zhang et al. used the self-consistent field (SCF) theory to study the phase behavior in mixtures involving cylindrical diblock copolymers and rigid nanorods.[32] Their results indicated that the novel morphologies of the mixtures clearly depended not only on the properties of the polymers but also on the number, length and surface adsorption (neutral, A and B attractive) of the nanorods. The results of this simulation study provide a theoretical guidance for the preparation of polymer nanocomposites. In addition to theoretical investigations, attention has been paid to experimental studies involving blends of nanorods in a polymer system. In recent years, Xu et al. showed that controlling the alignment of nanorods within BCP microdomains can be achieved by modifying the chemical properties and supramolecular morphology of the nanorods.[33] Wu and Lu[34] observed an arrangement of silver nanorods in thin films of immiscible polymer blends, which confirmed the theoretical study of Balazs et al. These findings can facilitate the fabrication of electrical and optical nanodevices. Experiments by Modestino demonstrated different self-assembly behaviors and vertically aligned CdSe nanorod arrays in polymer composites that can be obtained by controlling the interactions between the nanorod surfaces.[35] Jiang et al. studied the effects of gold nanorods (AuNRs) dispersed in homopolymer (P2VP) films. Their experimental results showed that the optical properties of a polymer nanocomposite can be adjusted by changing the volume fraction of the nanorods and the interaction distance between the individual rods.[36] Rasin et al. also experimentally examined the impacts of grafted gold nanorods (P2VP-AuNRs) on PS-b-P2VP thin films.[37] Their results showed the dispersion and alignment of AuNRs in a block copolymer thin film at sufficiently low concentrations, which have been validated by the polymer nanocomposite field theory. Meanwhile, there are many experimental[38–45] and theoretical studies[46–62] on the morphologies and phase behaviors of the block copolymer–nanorod system. Moreover, the bridging polymerization in the homopolymer solution in the presence of different interfacial attractions of polymer–particles has also been investigated in some studies.[63,64] As mentioned above, many research efforts have concentrated on the self-assembly of a block copolymer system. In addition, the self-assembly of mixtures of block copolymers and homopolymers in solvents has also been studied. The blend of C homopolymers and AB diblock copolymers can be shown to not only change the volume fraction of blocks in a facile way but also enrich the particle’s morphology. Using a simulated annealing method, Kong et al. studied the self-assembly of the blends of AB diblock copolymers and C homopolymers in a soft confinement. They discussed the effects of the confinement size, the volume fraction of polymer blocks, the selectivity of the confinement’s surface and the incompatibility between blocks on the self-assembly behavior of such systems. They obtained a variety of structures such as pupa-like, pine-cone-like, stacked disks and stacked lamellae. Their results were in accordance with the experiments.[65]
Inspired by these studies, we used cell dynamics simulation (CDS) to study phase transitions in a symmetric diblock copolymer–homopolymer hybrid system induced by nanorods with different properties and found many novel self-assembled structures. The CDS method was originally proposed in a series of work by Oono et al. to simulate the interfacial dynamics in the phase separation system. The characteristic of this method is that it quickly simulates the very complex dynamical behavior in large size phase separation systems and can predict new kinetic pathways. The CDS method has been widely used in many fields since it was put forward, for example, CDS studies of self-assembling phase behavior in diblock copolymers/diblock copolymer–homopolymer,[66–74] rock growth,[75,76] polymer crystallization [77,78] and polymer-dispersed liquid crystal.[79] The paper is organized as follows. In Section
To investigate the phase behavior of the mobile nanorods in a diblock copolymer–homopolymer hybrid system, we used a hybrid method of the Cahn–Hilliard (CH)/Brownian dynamics (BD) model, which has been extensively used by some researchers.[80–82] In this method, for the diblock copolymer–homopolymer hybrid system, we adopted the CH model. For the system of nanorods, we adopted the BD model. For the diblock copolymer–homopolymer hybrid system, its kinetic equation is highly complicated and its specific expression is as follows:
 |
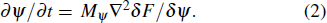 |
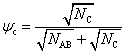
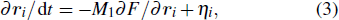 |
 |
The free energy F is composed of three parts F = FGL + FCPL + FRR. The free energy of a homopolymer/diblock copolymer is denoted by the Ginzburg–Landau free energy
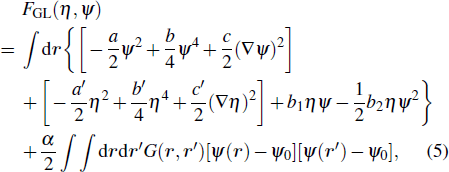 |

The FCPL describes the interactions between the nanorods and the polymer, and is given by
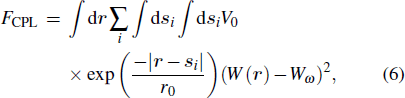 |
The FRR represents the interactions of the nanorods. In this paper, we assume that pure repulsion is dependent on the distance and angle between the pairs of rods i and j
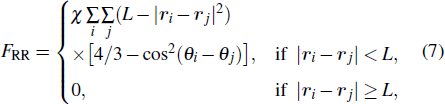 |
Figure
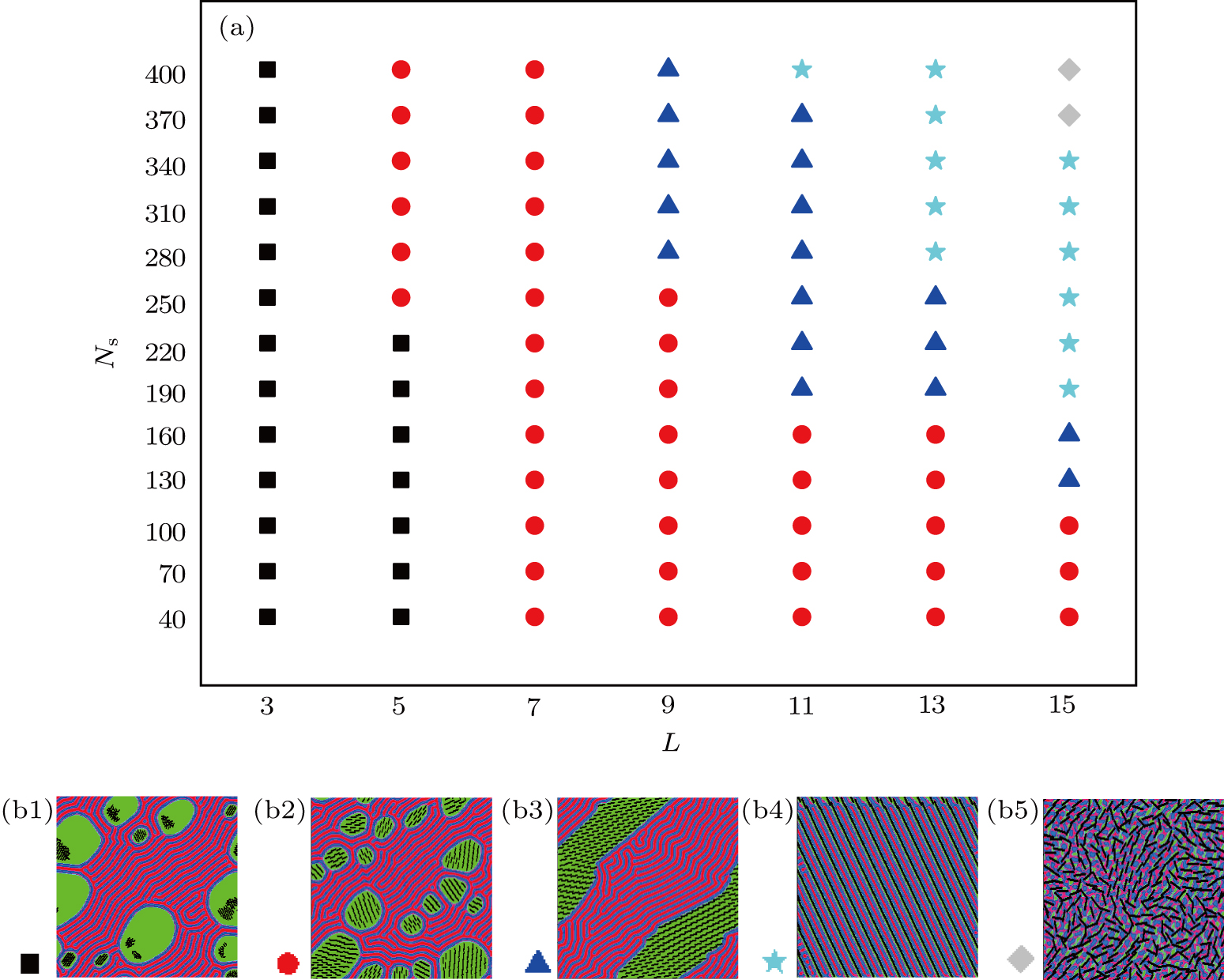
When the nanorods are dispersed into the diblock copolymer–homopolymer hybrid system, the system can self-assemble into phase-rich structures. Figure
From the phase diagram, we know that when the nanorods are short, they have a slight influence on the polymer system. So the polymer structure is similar to the AB/C bulk sea-island structure without the nanorods. When the length of the nanorods gradually increases, we can obviously see that the added nanorods have an influence on the polymer system and the sea-island structure of the original system is broken. The nanorods in the C domain align in an end-to-end structure, which is greatly influenced by the number of the nanorods. When the nanorods are few (40 < Ns < 100), they aggregate in the C domain. When there are some nanorods (100 ≤ Ns < 190), the nanorods disperse in the C domain and align end-to-end as a short nanowire. If the number density is small, it cannot form a large-scale nanowire structure. hence, it has a limited effect on the polymer system. When the number of nanorods is greater (Ns > 190), the system forms a nanowire structure through the whole range. The phenomenon can be explained as follows. Due to wetting interactions between the nanorods and the polymers, the nanorods are confined in the favorable C domains. When the nanorods are short, the weak repulsive interactions between them cause the rods to aggregate in the C component. As the length of the nanorods increased, the repulsive interactions become more obvious and result in them forming a parallel array of short-range nanowire structures in the C component. As the nanorod length is further increased, the interactions between the rods are enhanced as well, leading to the formation of a long end-to-end aligned nanowire structure throughout the region. Meanwhile, due to the interactions between the polymer components, the AB chains extend perpendicular to the macrophase interfaces that finally result in the formation of the nanowire structure. When the length and number of the nanorods exceed a certain limit, their interactions extend far beyond the constraints imposed by the C component, causing the nanorods to distribute over the whole area and form a disordered structure.
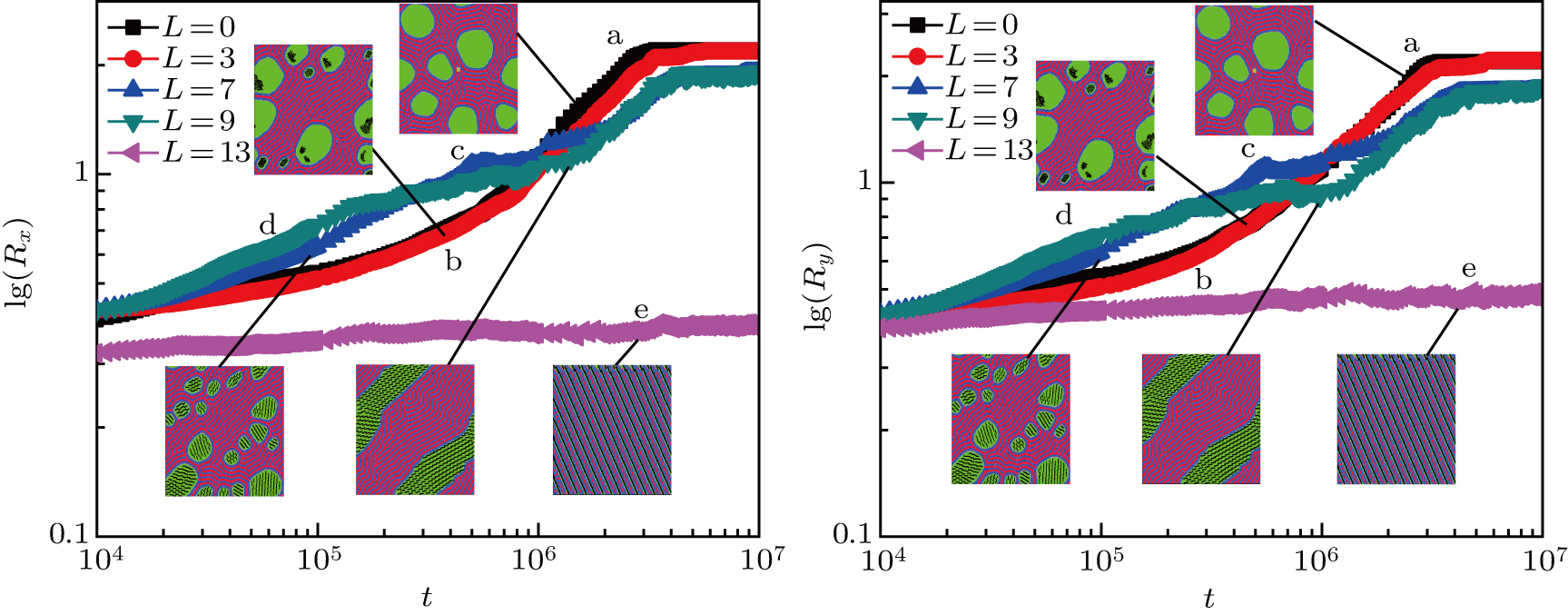
In order to quantitatively investigate the phase behaviors of the nanorods included in the diblock copolymer and homopolymer hybrid system, we numerically calculate the domain size R(t) in the x or y direction as a function of time. This is derived from the inverse of the first moment of the structure factor S(k,t) as Ri = 2π/⟨ki(t)⟩, where ⟨ ki(t)⟩ = ∫ dKkiS(K,t)/∫ dKS(K,t). The structure factor S(K,t) is determined by the Fourier component of the spatial concentration distribution. All results are averaged over 10 independent runs. Figure
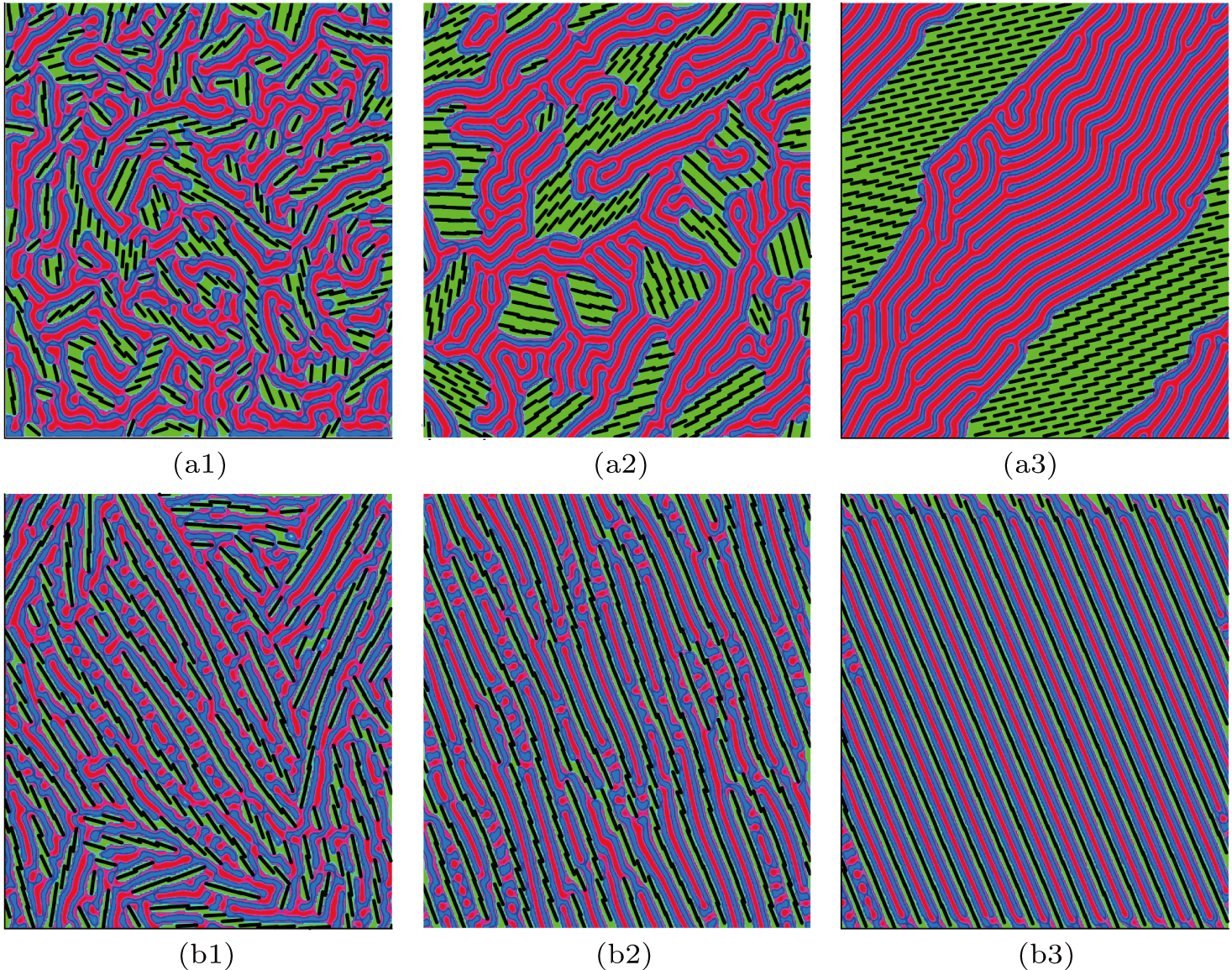
Furthermore, in order to explore the process of forming the ordered structure discussed above (Figs.
In order to further study the microscopic phase transition in the diblock copolymer–homopolymer system in the presence of nanorods, we show the histograms of the angular distribution of nanorods having different lengths for Ns = 340 in Fig.
 | Fig. 5. Angle of nanorods long axis direction and horizontal direction angle corresponding to (a) Ns = 340, L = 3, (b) Ns = 340, L = 7, (c) Ns = 340, L = 9, (d) Ns = 340, L = 13. |
In the meantime, we study the effect of the C component polymerization degree (NC) on the system structure. The results show that the polymerization degree of the C component has little effect on the system structure.
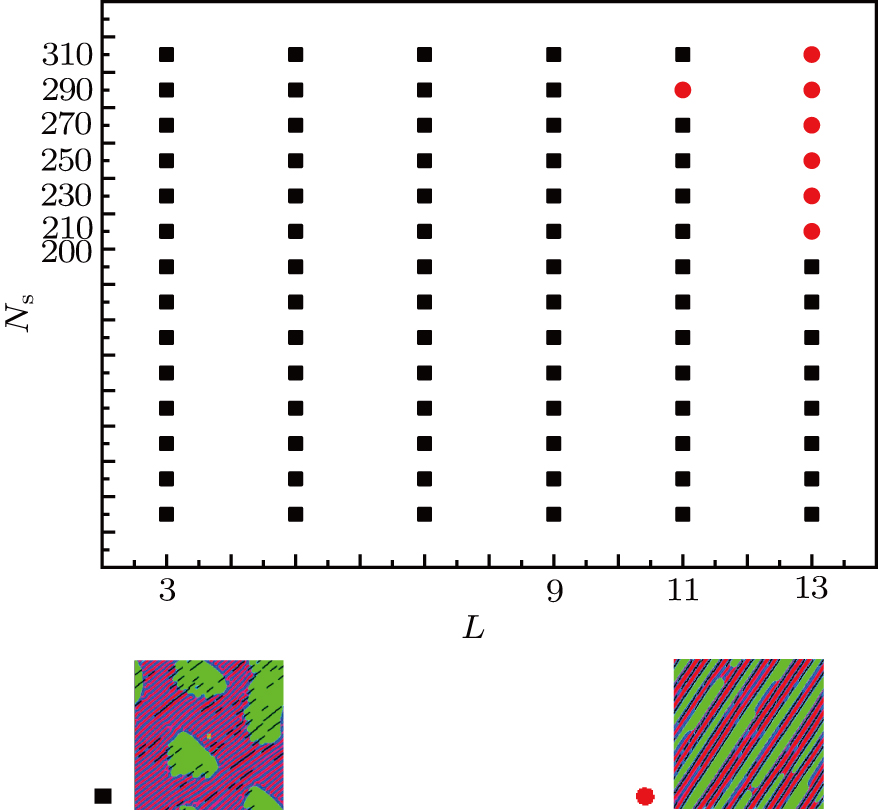
We consider the influence of different infiltration properties on the phase behavior of the system. For the nanorods infiltrating the B component of a diblock copolymer, we construct an approximate phase diagram as a function of their length and number. In the phase diagram shown in Fig.
We consider the effects of the different infiltration properties on the phase behavior of the system. For the nanorods having an affinity for the A block, we develop a phase diagram as a function of the nanorod number and length. In the phase diagram shown in Fig.
In summary, we used a computer simulation to study the phase transitions in a diblock copolymer–homopolymer hybrid system blended with nanorods. The results demonstrated that when the nanorods infiltrated the C component, the following system transformations occurred with the increase in the number of nanorods and length: (SI-G) to (SI-D) to (L-MP) to (L-SP) to (DIS). When the nanorods infiltrated the B component, a system transformation from the disordered structure to an ordered structure occurred as the number and length of the nanorods increased. When the nanorods infiltrated the A component, the increase in the number and length of the nanorods caused a system transformation from a disordered structure to an ordered structure. Meanwhile, we analyzed the evolution in pattern and the domain growth of these morphologies and structures. Our simulation provides a theoretical guidance for the preparation of an ordered nanowire structure and serves as a beneficial reference for improving the function of polymer nanocomposites.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] | |
| [64] | |
| [65] | |
| [66] | |
| [67] | |
| [68] | |
| [69] | |
| [70] | |
| [71] | |
| [72] | |
| [73] | |
| [74] | |
| [75] | |
| [76] | |
| [77] | |
| [78] | |
| [79] | |
| [80] | |
| [81] | |
| [82] | |
| [83] | |
| [84] | |
| [85] | |
| [86] | |
| [87] | |
| [88] | |
| [89] | |
| [90] | |
| [91] | |
| [92] |