Figure 2 displays the calculated scattering and absorption spectra of the SRR filled with silica glass. In the calculation, the refractive index of silica is used. There are quadrupolar and hexapolar resonances at 1499 nm and 983 nm, respectively. The modes are recognized by the charge distribution. Similar to Ref. [14], Fu et al. reported higher order Fano resonances in dual-disk ring plasmonic nanostructures and the Fano resonance via the quadrupolar ring mode was clearly observed in the charge distribution. The full width at half-maximum (FWHM) of the quadrupolar resonance peak is 135 nm and the quality factor is 11.1. The two resonance modes are very close to the absorption and emission peaks of the gain material co-doped with Yb³⁺: Er³⁺, hence the hexapolar resonance mode (983 nm) is set as the pumping mode and the quadrupolar one is set as the lasing mode (1499 nm).

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (color online) (a) The scattering and (b) absorption spectra of the SRR with no gain medium. The spatial distribution of the electric field amplitudes at the (c) quadrupolar and (d) hexapolar resonance modes.

The emission cross-section of rare earth ions is usually small, but it is still strong enough to support a plasmonic laser. Molina et al. demonstrated a Nd³⁺-based laser by means of localized surface plasmon resonances supported by chains of metallic nanoparticles.^[32] When the pump laser polarization was perpendicular to the chains, the quality factor was less than the value in our theoretical model.^[14,23] The experimental results indicated that the plasmon laser was rather bright when the pump laser power was larger than 225 mW.^[32] Nanoparticles co-doped with Yb³⁺:Er³⁺ and glasses have been demonstrated to be the most efficient emitting rare earth ions. Therefore, the gain is strong enough to generate a plasmonic laser in this system. Moreover, the gain material co-doped with Yb³⁺: Er³⁺ is just one example of a plasmonic laser used to detect single molecules.

Figures 2(c) and 2(d) show the electric field amplitudes on the SRR surface. The maximum electric field at the quadrupolar mode enhances up to 341 times and the hexapolar mode enhances up to 129 times. In addition, the intense electric fields of the two modes overlap very well in the SRR gap. These factors can intensify the absorption efficiency of the pumping light and improve the plasmonic lasing.^[35]

We also study the plasmonic properties of a ring resonator with the same parameters of the SRR except for the gap. When the wave vector of the incident light is perpendicular to the ring, the dipole resonance is excited, but the maximum electric field only enhances up to 56 times, which is much less than that of the SRR. For the oblique incident light, the multipolar resonances of a single ring can be excited, but they do not overlap in spatial distribution which hinders the simultaneous enhancements of the pump light and plasmonic lasing. Obviously, the SRR is a better choice to generate plasmonic lasing.

Figure 3(a) presents the calculated scattering and absorption spectra for different gain coefficient k. In this paper, all of the calculated scattering spectra for different k are normalized by the maximum scattering intensity with no gain material. Due to the narrow spectral range, the real part of the refractive index of the gain material is set as a constant of 1.5. The scattering intensity rapidly increases with k. The absorption becomes a negative value with increasing k, which means the ohmic loss is completely compensated by the gain medium. As k increases to the critical point k_c = 0.376577, the scattering intensity reaches the maximum value of 5.7 × 10¹⁰. The amplification of the surface plasmon is caused by the interaction among the incident light, the gain medium and the SRR.^[31] The gain medium absorbs energy from the pump light. It can provide the energy for the resonance loss compensation or amplification by nonradiative transition. These processes are further enhanced in return by the enhanced SRR resonance mode. When reaching the critical k_c, these processes achieve a dynamic balance and the plasmonic lasing operates effectively.^[36] If the gain coefficient k further increases, the light amplification will suppress the energy dissipation of the nanostructures. The dynamic balance is broken down and the scattering intensity greatly decreases. Figure 3(b) presents the dependences of the scattering intensity on the gain coefficient k.

Fig. 3.

	Figure Option ViewDownloadNew Window
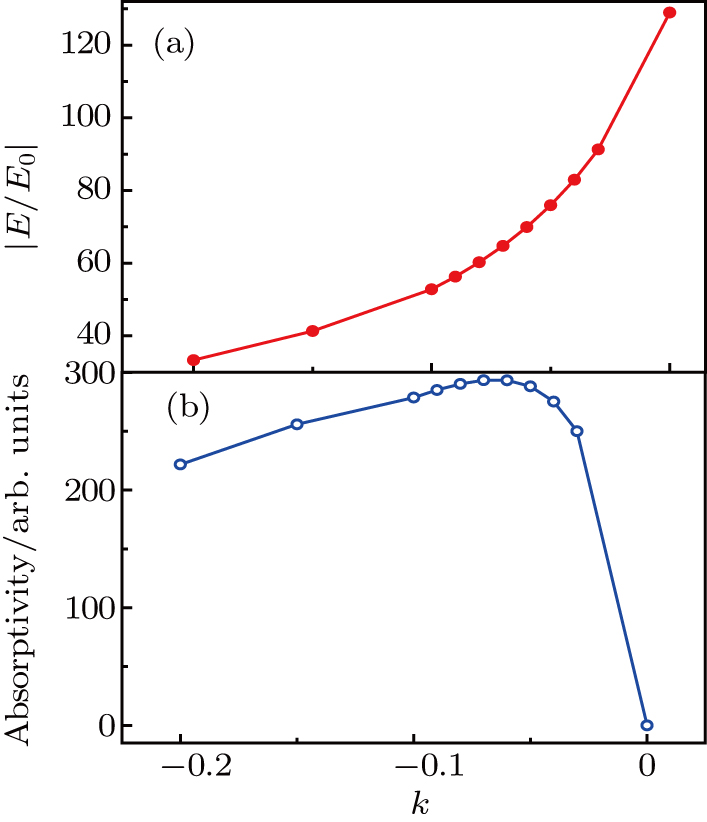
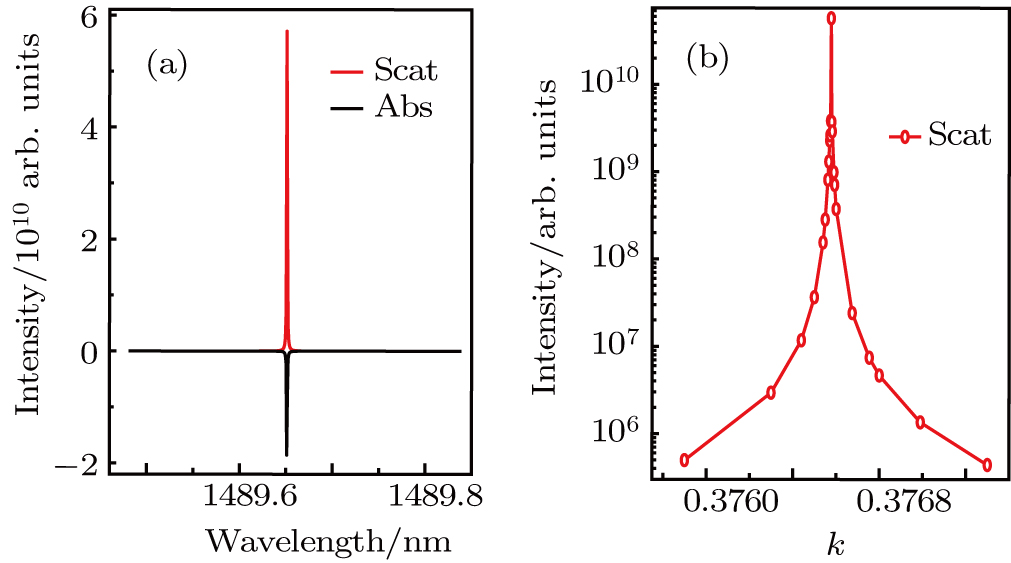	Fig. 3. (color online) (a) The scattering and absorption spectra for the gain coefficient k = 0.376577. (b) The dependence of the scattering intensity on k.

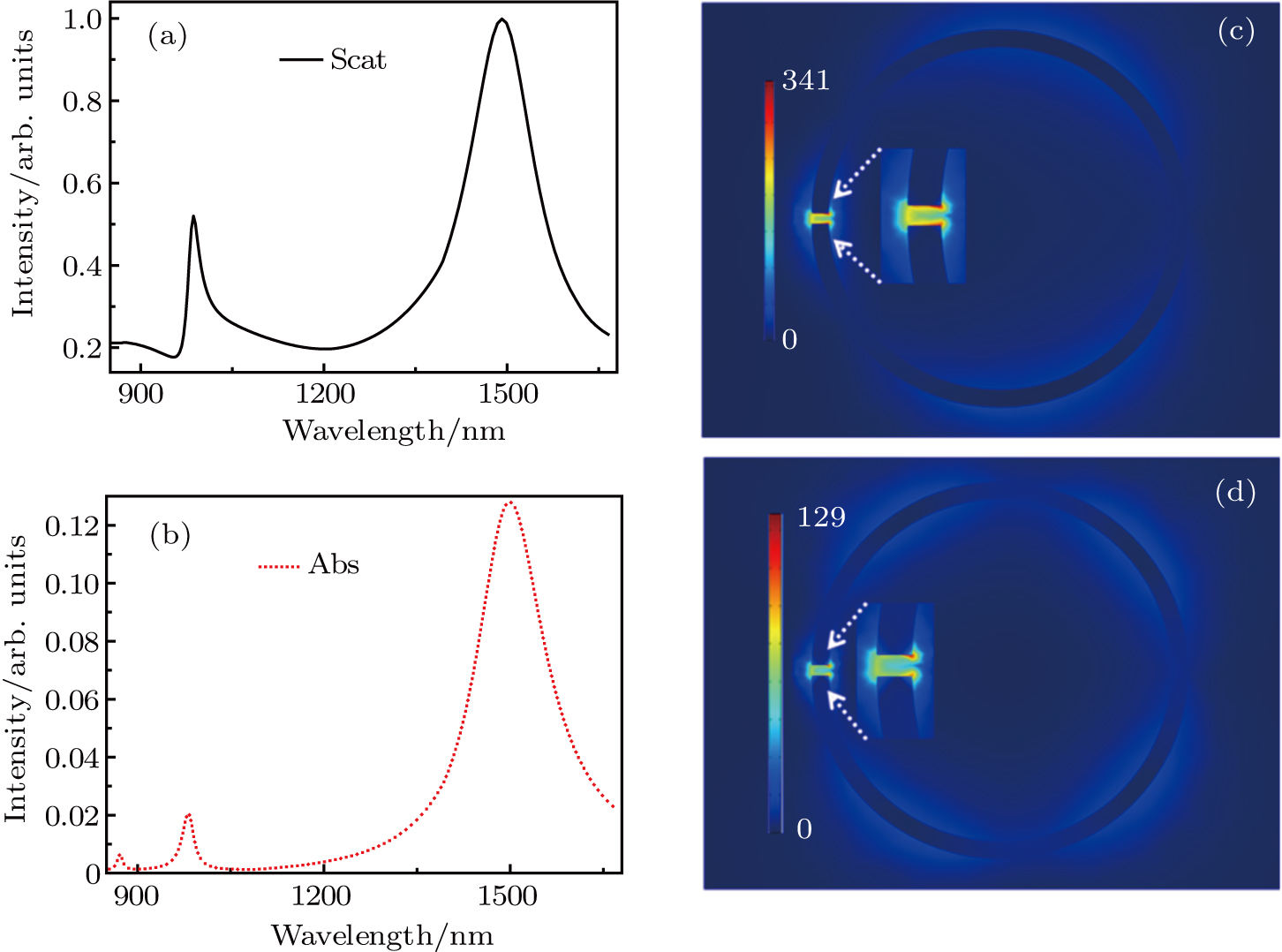
In the gain medium, because of a large absorption cross-section at 980 nm and a long excited-state lifetime, the Yb³⁺ ions efficiently absorb energy from the pump light and transfer the energy to the Er³⁺ ions. Electrons in the Er³⁺ ions damp to the ground state from the ⁴I_13/2 state, ^[33,34] and transfer the energy to the plasmon at the lasing wavelength by resonant coupled transition. However, the pump light is at the hexapolar resonance mode. Besides the pump light energy, the Yb³⁺ ions can also absorb resonant energy from the hexapolar plasmon. Figure 4(a) shows that the local electric field enhancement (LEFE) of the hexapolar resonance mode in the split ring gap increases with the extinction coefficient k. LEFE is defined as the maximum of the near-field enhancement |E/E₀|, where E and E₀ represent the electric field amplitudes in the gap and the incident light, respectively. The LEFE is reduced with the extinction coefficient decreasing because the gain material greatly absorbs energy from the pumping light via the resonant plasmon modes of the SRR. In the process of absorption of the pumping light, the energy transfer from the surface plasmon becomes strong, causing the decrease of the electric field enhancement. Therefore, the local field enhancement at the pumping light changes greatly with the imaginary part of the refractive index.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. (color online) (a) The dependences of LEFE and (b) the absorptivity on k.

High absorptivity of the gain medium is beneficial to obtain intense plasmonic lasing. The absorptivity is proportional to the extinction coefficient k and the pump light intensity. The pump light intensity in the SRR gap is proportional to the square of the LEFE. Hence the absorptivity of the gain medium is Abs∝ −k(E/E₀)². Figure 4(b) shows that the absorptivity increases as k decreases and reaches the maximum at k = −0.07. In this case, the LEFE is higher than 65 and the pump light intensity in the gap of the split ring can be increased by more than 4200 times.

For biomolecular detection, SRR plasmonic lasing has two special benefits. First, the pump light is far away from the lasing light, which can depress the noise coming from the pump light. Second, the lasing light and the pumping light are greatly enhanced simultaneously, which can greatly decrease the threshold of the pumping light and further reduce noise. Most importantly, biomolecules avoid being damaged.

The scattering spectra of the SRR plasmonic lasing are very sensitive to the surrounding material, which can be used as ultra-sensitive sensors. To investigate the sensing performance, we study the scattering spectra of the SRR nanostructure when nanoparticles are trapped in the gap.

Recently, many works have focused on the detection of protein molecules or viruses. The refractive indices of different types of proteins slightly change in the range of 1.45–1.5.^[37–39] In our model, we set the refractive index of the protein nanoparticle as 1.5. A monolayer protein is approximately 3-8 nm thick, which means the radius of the protein molecules is several nanometers as a sphere.^[39,40] Apart from biological molecules, the detection of polymer or semiconductor nanoparticles attracts a lot of attention.^[41,42] In this paper, we also study the cases of nanoparticles with refractive indices in the range of 1.7–3.

In SRR plasmonic lasing, the hot spot of the electric field is mainly located in the nanogap shown in Fig. 2. The laser intensity increases by more than 10³, as shown in Figs. 2 and 4. Therefore, the nanogap can trap the detected nanoparticle like an optical tweezer.^[3] In the calculation, the nanoparticle is located at the position shown in the inset of Fig. 5.

Fig. 5.

	Figure Option ViewDownloadNew Window
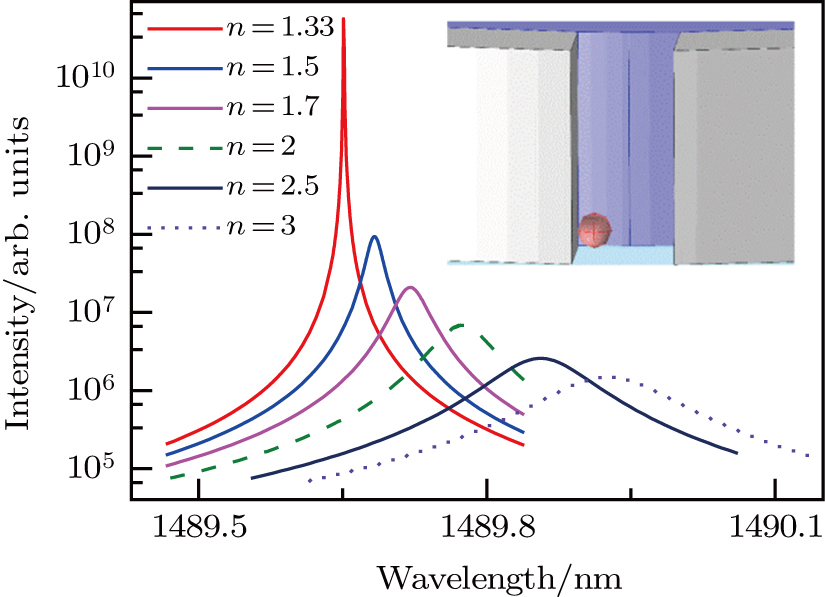	Fig. 5. (color online) Scattering spectra for different nanoparticles trapped in the gap. Here the nanoparticle radius is kept at 1.25 nm.

In order to avoid computation errors caused by re-meshing the geometry, we simply set the refraction index of the nanoparticle domain to be that of water in the case of no nanoparticle. The scattering intensity is as strong as 10¹⁰ and the FWHM is very narrow, only 0.01 nm. The peak of the lasing spectrum moves from 1489.652 nm to 1489.683 nm when a protein nanoparticle is attracted in the SRR gap, as shown in Fig. 5. The shift is 0.031 nm, which is much larger than the detection limit of the resonance wavelength shift of the plasmonic nanostructure of 10⁻⁵ nm.^[4] Even under the condition of the logarithmic graph, the two lasing spectra can be clearly separated. The scattering spectra for different analytic nanoparticles trapped in the gap are also shown in Fig. 5.

The detection precision is equal to the spectrum shift divided by the FWHM of the plasmon resonance. Recently, people tried many methods to reduce the FWHM of the scattering spectra. For example, Fano resonance is an important way to enhance the spectral detection resolution.^[43,44] In order to compare the detection precision of the SRR with or without a plasmonic laser, we study the scattering spectra of the SRR without gain material, which are shown in Fig. 2. The FWHM of the scattering spectrum is very wide, as large as 135 nm. In the case of the plasmonic laser, due to the metallic ohmic loss compensated by the gain medium, the FWHM is only 1/10⁴ of the case without gain material. Moreover, when a protein nanoparticle is trapped in the gap of the SRR without gain material, the shift of the scattering spectra is only 0.013 nm, less than one half of the case of plasmonic laser (0.031 nm). Therefore, the detection precision can be improved by more than 23000 times for the case of plasmonic laser.

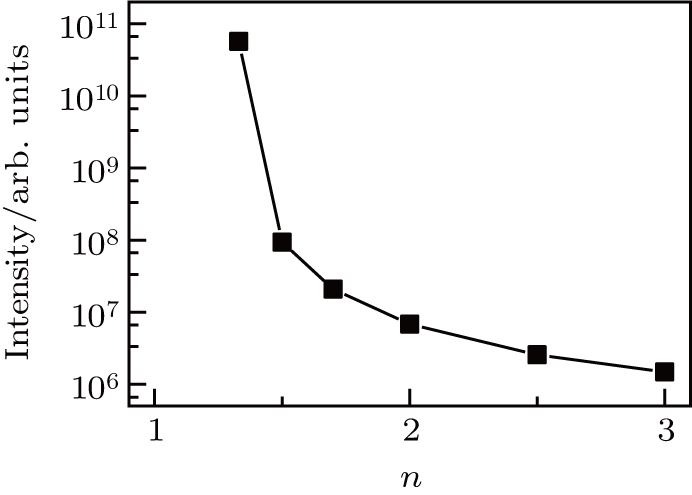
Ma et al. demonstrated that the lasing intensity was ultrasensitive to the adsorbed molecules. Figure 6 presents the scattering intensity for the trapped nanoparticle with different refractive indices. The scattering intensity is 5.71 × 10¹⁰, 9.43 × 10⁷, 2.08 × 10⁷, 3.82 × 10⁶, 2.58 × 10⁶ and 1.48 × 10⁶ for the refractive indices of 1.33, 1.5, 1.7, 2.0, 2.5 and 3.0, respectively. When a protein nanoparticle (n = 1.5) is trapped, the intensity reduces from 5.71 × 10¹⁰ to 9.43 × 10⁷, less than 1/600 of the intensity without any protein trapped, as shown in Fig. 6. Therefore, monitoring the change of the lasing intensity is also a very effective method. In brief, whether measuring the spectrum shift or the intensity, it is a very sensitivity method for label-free detection of single biomolecule with the SRR plasmonic lasing.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. The scattering intensity for the trapped nanoparticle with different refractive indices.

The detection of polymer (n = 1.7) or different semiconductor nanoparticles by the SRR plasmonic lasing is also studied. The scattering peak is redshifted due to hybridization of the split-ring plasmons.^[43] The shift of the resonance wavelength prevents the resonant energy transferring from the gain medium to plasmon, leading to a weak intensity and wide FWHM of the scattering spectrum. However, the lasing intensity is still as large as 10⁵ and the linewidth is only 0.135 nm for the nanoparticle with n = 3. Compared with the case of pure water, the lasing spectra move by 0.069, 0.123, 0.203 and 0.274 nm for the nanoparticle indexes n = 1.7, 2, 2.5 and 3, respectively. In each case, the shift of the lasing spectra is larger than its FWHM. Besides, the lasing intensities are 2.08 × 10⁷,6.82 × 10⁶,2.58 × 10⁶, and 1.48 × 10⁶, respectively, which are lower than the value of pure water by 2 to 3 orders. Obviously, the SRR plasmonic lasing is a superior method for detecting single polymer or semiconductor nanoparticles.

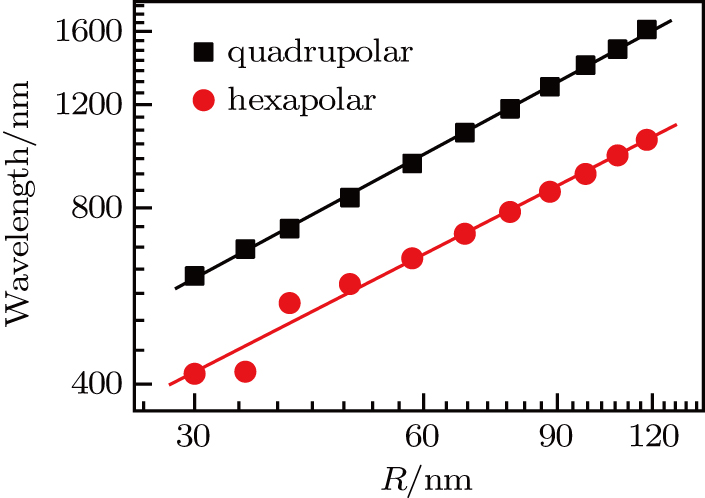
As illustrated in Fig. 7, the scattering peak systematically redshifts as the refractive index of the trapped nanoparticle increases. The sensitivity coefficient is defined as the resonance wavelength shift over the refractive index change unit (RIU), which usually indicates the ability of sensing. Linear regression analysis yields λ = 0.168 × (n − 1.33) + 1489.65 nm, namely, a refractive index sensitivity of 0.168 nm·RIU⁻¹.^[43,45] The plasmonic lasing wavelength linearly increases with the refractive index of the trapped nanoparticle, which is because the cavity eigenmode linearly changes with the refractive index based on the theory of dielectric microcavity systems.^[46,47] Zhang et al. further studied the resonance frequency shift for a plasmonic nanocavity trapping a single nanoparticle by using the perturbation theory,^[20] and revealed a linear dependence of the resonance frequency shift on the material dispersion factor. Experiments demonstrated a detection limit of spectral shift of 10⁻⁵ nm, from which we predict that the SRR plasmonic lasing can distinguish two single nanoparticles (r = 1.25 nm) when the refractive index changes only by 6 × 10⁻⁵.

Fig. 7.

	Figure Option ViewDownloadNew Window
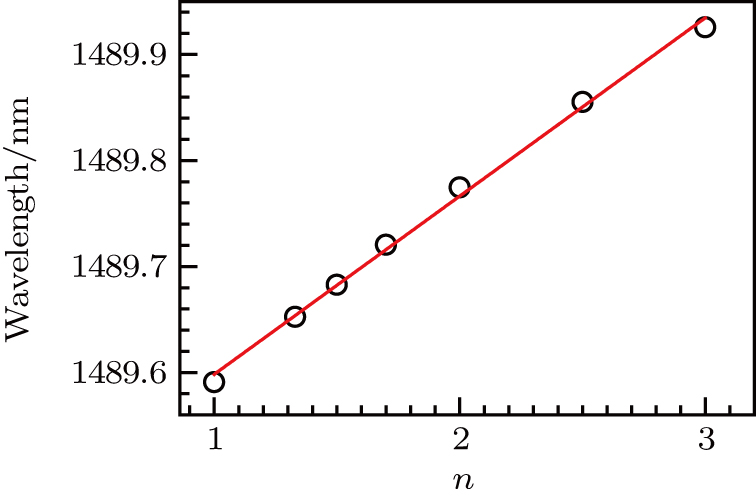	Fig. 7. (color online) The peak wavelength as a function of the refractive index n of the trapped nanoparticle. The red line depicts the linear fit.

Figure 8 presents the resonance wavelength shift with various numbers of protein nanoparticles with radius r = 1.25 nm. When four protein nanoparticles are trapped in the gap, the resonance wavelength shifts by 0.125 nm. The wavelength shifts by 0.031 nm after a nanoparticle is trapped in the SRR gap, which can be clearly distinguished. Therefore, the designed SRR plasmonic lasing can also be applied to multiple-molecule detection.

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. The resonance wavelength shift with varied numbers of protein nanoparticles. The inset shows the location of four nanoparticles.

We note that the diameter of the trapped nanoparticle is 2.5 nm and the nanogap width is 6.0 nm. Therefore, four nanoparticles can be trapped in the four designed positions. This is feasible in theory, though the exact positions slightly fluctuate.

The gap of the three-dimensional (3D) nanocrescent is 6.0 nm, which can be fabricated by several methods, such as electron-beam lithography, photochemical deposition and self-assembly nanofabrication.^[48–50] For example, Duan et al. have demonstrated nanoprism pairs of uniform sizes with systematic reduction of the gap to 0.5 nm and narrowing the bridge to 3.0 nm by using high-resolution electron-beam lithography.^[48] Ahmed et al. have reported a single antenna with a feed gap of 6.0 nm fabricated by a top-down approach and demonstrated single-molecule enhanced Raman scattering by taking advantage of the high local field enhancement in the nanogap.^[49] Moreover, Neubrech et al. proved that photochemical metal deposition onto lithographically fabricated nanoantenna can be used to decrease the gap between the nanoantenna dimers down to below 4.0 nm, which can realize new generation devices for ultrasensitive optical biosensing.^[50]

The diameter of the trapped nanoparticle is 2.5 nm and the nanogap width is 6.0 nm. That is to say, the width of the gap is larger than the double diameters. Therefore, four nanoparticles can be trapped in the four designed positions. Recently, Chen et al. studied surface-enhanced Raman scattering via a plasmonic nanogap of 2 nm between two Ag nanoparticles, while the molecule was modeled as a sphere of radius 1 nm and located at the nanogap center.^[51] Moreover, Arnold et al. predicted that the wavelength shift of whispering-gallery modes in microspheres by protein adsorption was proportional to the protein surface density.^[46] Thus, the wavelength shift becomes larger with increased numbers of nanoparticles.

Detecting a smaller molecule with a more sensitive method is the main objective in the field of single-molecule detection. For example, Dantham et al. reported the detection of single bovine serum albumin protein with mass of only 0.11 ag.^[4] This article theoretically provides a low-threshold, low-noise and high-intensity label-free single-molecule detection method. This method is based on spaser (surface plasmon amplification by stimulated emission of radiation), which can reduce damage to molecules and can be applied to the detection of living cells. For example, Galanzha et al. have demonstrated that a 22 nm spaser (plasmonic nanolaser) can be used as a super-bright, water-soluble, biocompatible probe, which can generate stimulated emission directly inside living cells and animal tissues.^[52]

Figure 9 demonstrates the scattering spectra of the nanoparticle with different sizes trapped in the SRR gap. Compared with pure water, the resonance wavelength shifts by 0.018 nm and the intensity is two orders lower when a protein nanoparticle with radius r = 1.0 nm is trapped. For the case of r = 0.3 nm, the resonance wavelength shift is 7 × 10⁻⁴ nm, which is much larger than the detection limit of 10⁻⁵ nm. Moreover, the scattering intensity decreases by half. Obviously, monitoring the scattering intensity is superior to the resonance wavelength shift.^[29]

Fig. 9.

	Figure Option ViewDownloadNew Window
	Fig. 9. (color online) The scattering spectra of a trapped nanoparticle with different sizes of (a) r = 1.0 nm and (b) r = 0.3 nm.

Figure 10 shows the resonance wavelength shift with varied sizes of protein nanoparticles. The linear fitting of the logarithmic dependences shows the relation of Δλ = 0.0184 × r ^2.54 nm, which means that the wavelength shift is nearly linear with the analytes volume. The fitting line shows that as the radius is only 0.1 nm, the wavelength shift is larger than 5 × 10⁻⁵ nm, which is still much larger than the detection limit of the biosensor platform.^[4] These results indicate that SRR plasmonic lasing can be used to detect small molecule with several atoms. In this paper, the quantum effect in the plasmonic system is out of our scope.

Fig. 10.

	Figure Option ViewDownloadNew Window
	Fig. 10. The resonance wavelength shift with the size of protein nanoparticle.

Broadband tunability is a critical driver for the practical application of plasmonic lasers. Recently, many plasmonic lasers with wavelengths from 489 nm to 1500 nm were demonstrated based on the gain materials of semiconductors (CdS, InGaAs, InGaN),^{[22, 24, 27]} organic dye (OG-488),^[23] rare earth ions (Nd³⁺),^[32] dye molecules (IR-140),^[53] and so on. Yang et al. achieved dynamic tuning of the plasmon lasing wavelength by modulating liquid gain materials with different refractive indices.^[53] To demonstrate broadband tunability, we change the outer radius of the SRR and keep the other geometric parameters constant. The results are shown in Fig. 11, where the SRR is filled with silica. The quadrupolar resonance mode can be changed from 612 nm to 1612 nm and the hexapolar is changed from 416 nm to 1044 nm when the outer radius varies from 30 nm to 118 nm. The resonance wavelengths change with the outer radius of the SRR because the local surface plasmon resonance is closely related to the nanostructure size.^[54] At the same time, both the electric field amplitudes at the two resonance modes are enhanced by hundreds of times, which indicates that the lasing light and the pumping light are both greatly enhanced. When the outer radius is smaller than 60 nm, the hybridization of different resonance modes occurs, causing fluctuations of the resonant wavelengths.^[55,56]

Fig. 11.

	Figure Option ViewDownloadNew Window
	Fig. 11. (color online) The resonance wavelengths as a function of the outer radius of the SRR.

In view of the effect of the optical tweezers, we mainly study the nanoparticle trapped at a point with strong electric field in the SRR gap. However, in actual applications, the nanoparticle moves back and forth in the gap. Due to the localized surface plasmon resonance and lighting rod effect, the maximum electric field is located in the gap.^[54,57] In order to further understand the influence of the trapped location, we study the spectra when the nanoparticle is trapped at different locations under the condition of plasmonic lasing. The middle inset shows four different locations of the nanoparticle (r = 1.25 nm) and they are labelled as 1 to 4, respectively. The left one is the electric field distribution on the middle surface and the right is that on the bottom surface of the SRR. Obviously, the electric field is more uniform on the middle surface, as shown in Fig. 12(a).

Fig. 12.

	Figure Option ViewDownloadNew Window
	Fig. 12. (color online) (a) Sketch of the electric field distribution on the middle and bottom surfaces of the SRR. (b)–(e) The scattering spectra for the nanoparticle trapped at four different locations shown in (a).

Figures 12(b)–12(e) are the scattering spectra for the nanoparticle trapped at locations ①–④, respectively. Similar to the case of Fig. 5, k is also kept at the critical k_c = 0.376577. The spectral intensities are normalized by the maximum scattering intensity with no gain material. The laser intensity becomes stronger because the loss is better compensated when the nanoparticle is trapped at locations ①–③. In the case shown in Fig. 12(e), the spectrum is narrow and strong for n = 1.33 because it is nearly a dynamic balance between the loss and amplification. The laser intensity randomly changes when the nanoparticles are trapped at different positions because of the uneven electric field distribution. Baaske et al. have reported that the sensitivity can be understood from theoretical predictions of plasmonic field enhancement and a molecule that bound within a plasmonic hotspot tuned the resonance wavelength in proportion to the enhanced field strength encountered at the binding site.^[5] Zhang et al. reported that to achieve high sensitivity, one needs to generate a large local electric field intensity.^[20] The case of spectral shift is much different. The results indicate that when the nanoparticle is trapped at the four locations, the laser spectral shifts are 0.029 nm, 0.022 nm, 0.030 nm and 0.023 nm, respectively. Our calculation results indicate that when a nanoparticle is adsorbed at different locations in the gap, the spectral shifts are in the range of 0.020–0.032 nm because of the coupling with the uneven electric field. Therefore, a trapped nanoparticle can be monitored by the spectral shift.

During the fabrication of the SRR, the gap is usually etched into a wedged shape, as shown in Fig. 13(a). The top width of the gap is W_u and the bottom is W_d and their difference is d = W_u − W_d. Figure 13 shows the scattering spectra for a protein nanoparticle trapped in the wedged gape, where d changes in the range of 0–10 nm while W_d is kept as 6 nm. The spectral shifts are 0.0358 nm, 0.0395 nm and 0.0437 nm when d are 2 nm, 5 nm and 10 nm, respectively. The shift becomes larger with d increasing. The reason is that the bottom edge of the gap becomes relatively sharper as d increases and the electric field becomes stronger. In the calculation of Fig. 13, the nanoparticle is trapped at the bottom edge, as shown in the inset of Fig. 5. Therefore, the wedged gap can be well used in the detection of the trapped nanoparticle. It is helpful in reducing the difficulty of nanofabrication and is more suitable for biological detection in the future.

Fig. 13.

	Figure Option ViewDownloadNew Window
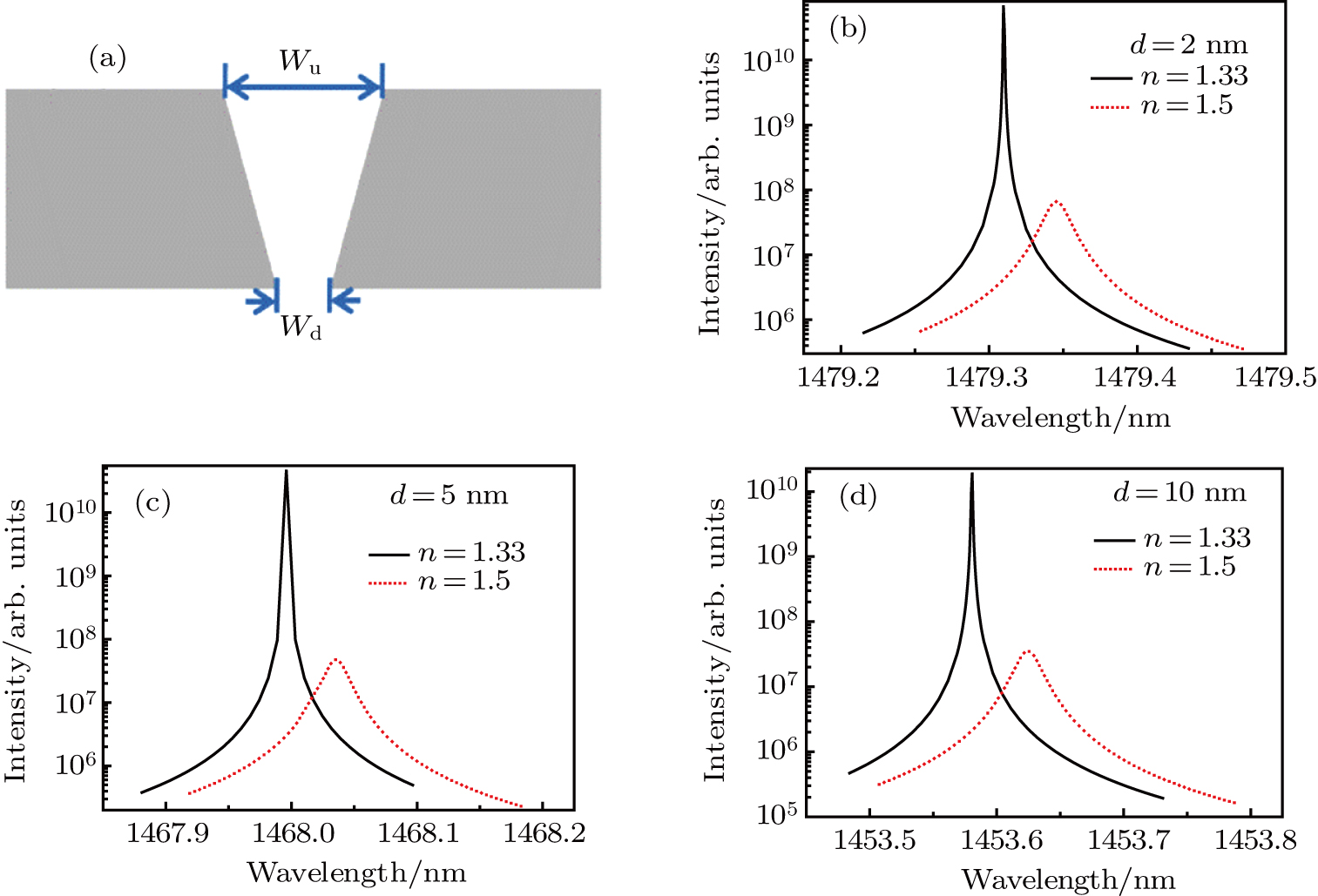	Fig. 13. (color online) (a) The cross-section of the waged gap. (b)–(d) The scattering spectra for d = 2 nm, 5 nm and 10 nm, respectively. The trapped nanoparticle has n = 1.5 and r = 1.25 nm.

The case of W_u less than W_d is also studied. When W_u is less than W_d, for example, when d = −1 nm and −2 nm, the spectral shifts are 0.0299 nm and 0.0264 nm, respectively. The spectral shift becomes smaller because of sharpness decreasing for the lower edge of the gap. Moreover, Dantham et al. found that the wavelength shift due to the single protein adsorption mainly depended upon the electric field intensity at the surface of the bump.^[4] As a result, the electric field is mainly located at the upper edge, rather than the lower edge of the gap.^[54] The coupling between the split ring and the nanoparticle becomes weak and the shift becomes smaller.