Spintronics is currently a very active research field in condensed matter physics, aiming to exploit both the charge and spin degrees of freedom of electrons in the new generation of spin-based devices.^[1] Since graphene has many important properties with high application potentials, such as the gate voltage-controlled carrier conduction and high mobilities, spin currents generated or manipulated in graphene have attracted a great deal of research attention.^[2–6] Especially, the weak spin–orbital interaction and the lack of nuclear spin in graphene will enable the maintenance of spin coherence over longer distances than that in conventional semiconductors. An experiment^[7] on spin injection into single layer graphene found that the spin coherence length is about 1 μm in dirty samples and a much longer coherence length is expected in a clean system. This is also attributed to the properties of the massless Dirac electrons with linear energy dispersion.

Silicene, similar to graphene, is a monolayer of silicon atoms instead of carbon atoms assembled into a two-dimensional (2D) honeycomb lattice and also, electrons in silicene around the Fermi energy are linearly dispersed. Recently, this material has been experimentally synthesized and theoretically explored.^[8–13] Different from graphene, silicene has a prominent buckled structure that the A and B silicon atoms are not coplanar, which allows one to control the mass of the Dirac electrons by a perpendicular electric field and leads to some peculiar transport properties of electrons in silicene. Therefore, the generation and manipulation of spin currents of Dirac electrons in the silicene system are similarly very attractive.

Quantum spin and charge pump is a striking topic in the context of quantum transport through nanostructures.^[14–16] The nature of the quantum parameter pump arises from the geometric Berry phases and quantum interference effects. Generally, a nonzero pumped current can be generated in a pump device with at least two pumping parameters out of phase. In the adiabaticity that the characteristic time of the parameter variations is much shorter than the dwell time of the carriers, the pumped current is proportional to the geometric area circled by the time-dependent parameters.^[16] Quantum parameter pump is a significant and effective means to generate spin currents.^[17–22]

In this work, we propose to generate spin currents in a two-parameter pump device based on silicene, where the pumping potentials are simulated by the time-dependent perpendicular electric field applied to the system, while a magnetic insulator is assumed in between the two pumping potentials to induce possible magnetization. It is shown that the device can pump out spin currents, including both pure spin currents and fully spin-polarized charge current. Due to the quantum interference effect, the pumped spin currents can be modulated by controlling the magnetization parameters. When the Fermi energy is residing in the energy gap of the pumping potentials, the pumped currents are maximized.

Let us start from a silicene-based pump device as schematically shown in Fig. 1, where the two staggered pumping potentials Δ₁ and Δ₂ are assumed from the time-dependent perpendicular electric field E_z with Δ_1,2 = E_zl and l being the perpendicular distance between the A and B silicon atom planes, and a magnetic insulator^[23] (say, EuO) is deposited on the silicene between the two pumping potentials with a length L₀. Thus, a constant magnetization M is assumed to be induced in the silicene. The whole pump device is connected to the outside world through the left and right electrodes but without any bias. The sizes of the two pumping potentials are marked by their lengths L along the current direction (the x-axis) and the transverse direction (along the y-axis) is assumed homogeneous or to have a translational symmetry.

Fig. 1.

Figure Option ViewDownloadNew Window

Fig. 1. (color online) Schematic of a two-terminal pump device based on a monolayer silicene. The two pumping sources, Δ1 = Δ0 cosωt and Δ1 = Δ0 cos(ωt + ϕ), are the staggered potentials with a phase lag ϕ between them. The pumped current direction is assumed along the x axis and the device is connected to electrodes through the left and right leads. L is the length of the pump region and L0 is the length of the magnetic insulator M inserted between Δ1 and Δ2.

A low-energy continuum Hamiltonian is adopted here to describe the pump device as^[24]

In the adiabatic limit ω → 0, the pumped current can be calculated directly from the BPT formula as^[26]

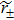
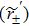
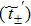
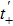
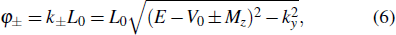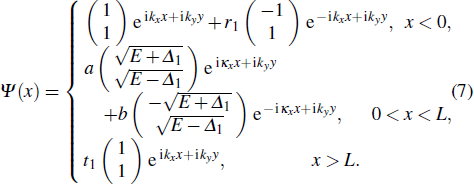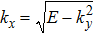
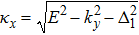
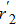
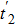
In order to work out the scattering coefficients, one can construct a single scattering process to solve them directly or choose the following combining method to obtain them. We have the formulae of two relevant coefficients r_± and through two individual scattering events at Δ₁ or Δ₂ potentials,

With these preparations above, we can directly calculate the spin-resolved pumped current I_L↑(↓) (± = ↑(↓)) flowing through the left lead of the pump device in Fig. 1 according to Eq. (3). We set ℏv_F = 1, so the Fermi energy E, the momentum k_x(k_y), and the magnetization strength M have the same energy unit for simplicity. Since the quantized pumped current is focused on, in that the Fermi energy resides in the energy gap opened by Δ₁ and Δ₂, and the transverse momentum k_y does not bring any qualitative effect on the results, we can, for simplicity, consider a pure one-dimensional case k_y = 0.

We first plot the pumped current (I_L) versus the pumping phase ϕ and the results are shown in Fig. 2. The curves deviate from the usual sine function behavior of an adiabatic quantum parameter pump I ∼ sinϕ, since the pumped current obtained here is quantized as the Fermi energy is taken as E ≪ Δ₀, i.e., I_L↑,↓ = ±e/T. One can see that in Fig. 2(a), the spin-up and spin-down pumped currents are almost opposite, which implies that the pump device can pump out pure spin currents. Whereas in Fig. 2(b), the magnetization is changed from M = 0.003 eV to M = 0.01 eV, both spin species currents are almost the same so that pure spin current almost vanishes.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (color online) Spin-resolved pumped current–phase relationship IL ∼ ϕ. The magnetization strength is (a) M = 0.003 eV and (b) M = 0.01 eV. Other parameters are E = 0.001 eV, Δ0 = 0.01 eV, L = 1000a, and L0 = 1000a with a being the lattice constant.

The quantization of the pumped currents is ascribed to the possible topological interface state^[25] forming between the two pumping potentials, which is evolving with time. As mentioned above, the staggered potential will result in a topological valley Hall phase appearing in the pumping region, but this topological phase state has no boundary or edge state. However, such an interface state with zero energy will appear in the bridging region when Δ₁ and Δ₂ have the opposite signs. It is this topological interface state that leads to a nonzero pumped current as well as its quantization when the Fermi energy locates in the energy gap. Otherwise, an insulator would not conduct any current. When ϕ ∼ nπ, the pumped current is deviated from the quantized value e/T in Fig. 2. The reason is that the effective energy gap is quite small so that the Fermi energy locates outside of the energy gap.

Since the pumping effect is in nature a quantum interference effect, the pumping results can be modulated by the dynamic phase of the electrons. Therefore, it is shown that different magnetization M will lead to different spin-dependent pumped currents I_L↑/I_L↓ and this is attributed to the different phase φ_± in Eq. (6). So we can obtain pure spin currents in the studied pump device. According to this reasoning, one can also utilize the length L₀ of the magnetization region to control the pumping output and instead, we choose to modulate the overall potential profile V₀ to change the pumped spin currents.

In Fig. 3, the spin-dependent currents are presented as a function of V₀ with different lengths L₀. It is seen that the spin degeneracy is broken by M and the spin-up and spin-down momenta in the magnetized silicene are split and changed by V₀, so that one can obtain a nonzero spin current I_s = I_L↑ − I_L↓, and even a fully spin-polarized current with I_L↑ = 0 or I_L↓ = 0. Since V₀ is varied, the electron momentum in the magnetization region would change accordingly so as to the dynamic phase φ_±. From this, one can also see that even the variation of the Fermi energy can modulate the pumped spin currents too, because E and V₀ play the same roles in determining φ_±. Similarly, it is not strange that when L₀ is different, the periodicity of the pumped spin currents with V₀ should also be different as shown in Figs. 3(a) and 3(b); the larger the L₀, the shorter the V₀ periodicity.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (color online) Pumped current IL as a function of the gate voltage V0. The length of the magnetization region is (a) L0 = 1000a and (b) L0 = 500a. Other parameters are E = 0.001 eV, Δ0 = 0.01 eV, ϕ = π/2, L = 1000a, and M = 0.005 eV.

It is worth pointing out that it is not uncommon to obtain pumped spin currents in a device with magnetization involved, nevertheless, the studied model can provide an optimal pumping effect of spin currents, i.e., for each transport model, the pumped spin is maximized. Moreover, when the Fermi energy E locates in the energy gap ∼Δ₀, the pumping is quantized^[25] for all transverse modes k_y. Although the magnetization introduced in the pumping device here is limited between the two pumping devices, this is not compulsory and it can extend to all devices. The key point to spin currents is the spin-splitted momentum in the normal silicene region without pumping potentials resulting in an energy gap of silicene. We have discussed the optimal spin currents pumped in a silicene-based device by using the time-dependent electric fields that induce the staggered potentials. Actually, such a conclusion is also valid in a graphene-based device by using the time-dependent strains, which can play the same role as the staggered potentials, however, the transport direction is quite important since the graphene cannot have a transport gap along all directions, which is necessary for the quantized pump.

We have investigated the pumped spin currents in a silicene-based pump device. The pumping potentials are from the perpendicular electric fields that result in the staggered potentials in the silicene and the magnetization is assumed to be induced by the magnetic proximity effect. According to the adiabatic pumping theory, we calculated the pumped currents flowing in the device and found that the currents are quantized when the Fermi energy resides in the energy gap opened by the staggered potentials. The pure spin currents and fully spin-polarized currents can be obtained by modulating the relevant parameters such as the Fermi energy and the magnetization strength. Our findings are helpful to generate spin currents in the Dirac-electron system.