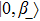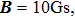1. IntroductionThe negatively charged nitrogen-vacancy (NV) color center[1,2] in diamond has attracted great interest from various quantum information processing (QIP) applications[3–8] to high-resolution sensing of magnetic field[9,10] and imaging in life science[11] by using ODMR technique,[12] even at room temperature. Specifically, NV center has become a prominent magnetometer, the central idea of which is detecting the relative energy shift of ground state by an external AC or DC vector magnetic field.[9,10,13,14] By detecting frequency and relevant shift, the corresponding parameters of external magnetic field could be precisely determined. The information of strength and polar angle of vector magnetic field (relative to NV symmetry axis) could be easily extracted by observing two resonance frequencies of continuous wave (CW) spectrums, but the information of azimuth angle is still missing due to the
 symmetry of the defect. One solution to this issue is that NVs were employed in a multi-NV vector magnetometer with different
symmetry of the defect. One solution to this issue is that NVs were employed in a multi-NV vector magnetometer with different
 axes.[13,15] However, these NVs are the best to be close to each other and differ by no more than hundreds of nanometers for achieving high spatial resolution. Another alternative strategy, suggested theoretically by Ref. [16], only used a single high-spin system (such as SiC with spin 3/2) as a vector magnetometer, which might further improve the spatial resolution.
axes.[13,15] However, these NVs are the best to be close to each other and differ by no more than hundreds of nanometers for achieving high spatial resolution. Another alternative strategy, suggested theoretically by Ref. [16], only used a single high-spin system (such as SiC with spin 3/2) as a vector magnetometer, which might further improve the spatial resolution.
In this paper, using a single NV center with a single first-shell 13C nuclear spin (NV–13C), an executable experiment scheme of detecting a static vector magnetic field is proposed in diamond. More information of vector magnetic field could be revealed by resonance spectrum. The reason is that the symmetry of the NV–13C can be reduced from
 to
to
 , a single mirror plane. Moreover, the energy level splitting of 13C nuclear spin is sensitive to the changes of external magnetic field in contrast to 14N nuclear spin, which remains almost unchanged. Due to the distance between 13C nucleus and NV electron less than 1 nm, the advantage of our proposal is that high spatial resolution conditioning precise measured hyperfine coupling tensor of NV–13C,[17–21] high contrast of the fluorescent readout, and narrow linewidth of resonance spectrum lines[22] may be achieved by experimental implementation.
, a single mirror plane. Moreover, the energy level splitting of 13C nuclear spin is sensitive to the changes of external magnetic field in contrast to 14N nuclear spin, which remains almost unchanged. Due to the distance between 13C nucleus and NV electron less than 1 nm, the advantage of our proposal is that high spatial resolution conditioning precise measured hyperfine coupling tensor of NV–13C,[17–21] high contrast of the fluorescent readout, and narrow linewidth of resonance spectrum lines[22] may be achieved by experimental implementation.
2. A static vector magnetic field detection with an NV–13C2.1. The NV–13C systemAn NV–13C sensor consists of a substitutional 14N and a nearest neighbor 13C nuclear spins adjacent to the vacancy defect. The spin Hamiltonian of the system under an applied static vector magnetic field
 can be written in a coordinate system, in which the NV axis is aligned to z axis, and x axis lies in the plane constructed by 14N–V–13C (seen in Fig. 1). The combined spin system can be written by Hamiltonian
can be written in a coordinate system, in which the NV axis is aligned to z axis, and x axis lies in the plane constructed by 14N–V–13C (seen in Fig. 1). The combined spin system can be written by Hamiltonian
where vector magnetic field

can be expended to

,
θ and
ϕ are the polar and the azimuth angles relative to
z and
x axes in the NV frame of reference, respectively. The gyromagnetic ratios of NV electron,
13C and
14N nuclear spins are

,

, and

, respectively. Zero-field splitting
D and quadrupole splitting
P of
14N correspond to 2.87 GHz and −5 MHz, respectively. The last two terms of Eq. (
1) respectively represent the NV electron spin coupled to
14N and proximal
13C nuclear spin. Since the hyperfine splitting of
14N nuclear spin (spin
I = 1) is a constant of −2.16 MHz
[23] and insensitive to changes of applied vector magnetic field, we could only consider the hyperfine structure of NV spin coupled to the
13C nucleus written as
where the NV–
13C hyperfine interaction

is

, when choosing the
x axis such that

without lack of generality. From Eq. (
2), eigenvalues

in descending order and corresponding eigenvectors

of ground state can be obtained. For sub-manifold

with the hyperfine splitting of
13C nuclear spin, the relevant eigenvectors

could be approximately equal to

, where the
13C nuclear spin states

could be approximated as

with

.
[24] The ordering of the corresponding energy level of eigenvectors

could be exchanged by the switching of polar angle
θ between

and

For sub-manifold

, its corresponding eigenvectors

could be approximately equal to

in which the nuclear states

of interest depended entirely on applied vector magnetic field and could be written as

Concrete schematic diagram can refer to Appendix A. Specifically, the quantization axis of sub-manifold
ms = 0 and corresponding spin dynamics could be affected by the microwave power strength.
2.2. The determination of eight candidated hyperfine tensors for a single NV–13CIn the NV–13C frame of reference, the symmetric hyperfine tensor
associated with the nearest
13C coupled to NV spin, was determined in Ref. [
19], where

for

is the component of eight candidated hyperfine tensors,

. The components are listed in Appendix B, in which the signs of

can be positive or negative, and can be linked by a
π rotation transformation around the
z axis.
However, when NV–13C is used as a vector magnetometer, its hyperfine tensor should be uniquely identified instead of multiple candidates due to mirror symmetry. A simple scheme may be feasible as an initial state of NV electron spin
 with 13C nuclear spin state
with 13C nuclear spin state
 is polarized[1,24] and prepared. Under an applied magnetic field
is polarized[1,24] and prepared. Under an applied magnetic field
 aligned along the NV–13C axis (z-axis), its total free evolution under the Hamiltonian (2) demonstrates eight different evolution processes conditioned the chosen hyperfine tensor. The evolving states are projected onto the state
aligned along the NV–13C axis (z-axis), its total free evolution under the Hamiltonian (2) demonstrates eight different evolution processes conditioned the chosen hyperfine tensor. The evolving states are projected onto the state
 with evolving populations as shown in Fig. 2. Along the way, in experiment one needs to observe the free induction decay (FID) signal of the NV–13C. 3
with evolving populations as shown in Fig. 2. Along the way, in experiment one needs to observe the free induction decay (FID) signal of the NV–13C. 3
2.3. The spin dynamics of ground state under microwave fieldA microwave (MW) field is applied and causes transitions between the electron spin levels, which modulates the fluorescence intensity. At relative low microwave power, the hyperfine splitting of
 corresponds to two eigenstates of
corresponds to two eigenstates of
 and
and
 between which the analytic form
between which the analytic form
of the effective Larmor splitting obtained by the second order perturbation theory reveals the direction of applied vector field.
[18] Through numerical calculations in moderate magnetic field (

), the above approximate formula of
Δ conforms well to the numerical results based on Eq. (
2). In the remaining cases of relatively high MW power, the Larmor splitting of sub-manifold
ms = 0 corresponds to two linear superposition states

of eigenstates

and
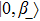
, whose quantization axis of nuclear spin is realigned to a new axis defined by nuclear spin states

.
[24]At relatively low MW power, the doublet transitions between
 and
and
 could be observed. Taking into account the hyperfine splitting of the 14N nucleus, the double peak transitions above could further show six resonance lines as demonstrated schematically in Fig. 4(a). With the increase of MW power, only a single peak transition could be observed and its resonance frequency is almost centred between the doublet transitions of
could be observed. Taking into account the hyperfine splitting of the 14N nucleus, the double peak transitions above could further show six resonance lines as demonstrated schematically in Fig. 4(a). With the increase of MW power, only a single peak transition could be observed and its resonance frequency is almost centred between the doublet transitions of
 as shown in Fig. 4(b).
as shown in Fig. 4(b).
2.4. Numerical simulations of a static vector magnetic field detection2.4.2. The fault tolerance analysis of NV–13C sensorThe four resonance frequencies
 of electron spin are sensitive to the changes of polar angle θ, compared to its insensitivity of the changes of azimuth angle ϕ. However, the Larmor splitting Δ induced by 13C nuclear spin is sensitive to the changes of ϕ as shown in Fig. 5. Thus, to precisely detect a static vector magnetic field, both the two factors of
of electron spin are sensitive to the changes of polar angle θ, compared to its insensitivity of the changes of azimuth angle ϕ. However, the Larmor splitting Δ induced by 13C nuclear spin is sensitive to the changes of ϕ as shown in Fig. 5. Thus, to precisely detect a static vector magnetic field, both the two factors of
 and Δ should be taken into consideration.
and Δ should be taken into consideration.
With a method akin to maximum likelihood estimation, our simulations implemented a numerical search procedure to match both the target four measured resonance frequencies
 and the measured Larmor splitting Δ as shown in Fig. 4 according to the formula similar to[13]
and the measured Larmor splitting Δ as shown in Fig. 4 according to the formula similar to[13]
where the

and
Δ have linewidth

and
δΔ, respectively. The linewidth
δ is fundamentally limited by the imhomogeneous dephasing rate,

of the NV electron spin, which is decided by magnetic dipolar interactions with a bath of nuclear spin in diamond. The pulsed-ESR spectrum linewidth

is inversely proportional to the
π-pulse duration limited by

. Furthermore, the linewidth could also be affected by power broadening, which is from the laser used for initializing electron spin and MW field used for spin manipulation. Thus, in experiment, the laser intensity and MW power should be decreased appropriately for achieving a sharpen linewidth.
[22] For Larmor splitting

Ramesy sequence could achieve sharper linewidth

. Therefore, we introduced random measurement errors

and

limited by linewidth

and

. One could pick the parameters

,

, and
B0 satisfying
that minimizes Eq. (
3), compared to other choices of parameters. The search ranges of direction parameters

are set to

and

respectively.
With above method, the simulations of detecting vector direction with fixed
 are carried out and results are given in Fig. 6, where random measurement errors
are carried out and results are given in Fig. 6, where random measurement errors
 and
and
 are introduced. It should be noted that for large misalignment angle θ relative to the z axis, high resolution of azimuth angle ϕ may be easily achieved compared to those of small misalignment angle θ. At the same time, relatively higher magnetic field strength could improve the angular resolution of detected
are introduced. It should be noted that for large misalignment angle θ relative to the z axis, high resolution of azimuth angle ϕ may be easily achieved compared to those of small misalignment angle θ. At the same time, relatively higher magnetic field strength could improve the angular resolution of detected
 due to the higher resolution of Larmor splitting Δ for different azimuth angles ϕ as shown in Figs. 5(a) and 6(c).
due to the higher resolution of Larmor splitting Δ for different azimuth angles ϕ as shown in Figs. 5(a) and 6(c).
Next, taking into account the errors
 of hyperfine components referred in Appendix A, we found that for large misalignment angle θ relative to the NV–13C axis, simulated field strength
of hyperfine components referred in Appendix A, we found that for large misalignment angle θ relative to the NV–13C axis, simulated field strength
 and direction angle (θ, ϕ) were robust against these errors compared to those of small ones. Detailed numerical comparison would not be listed here.
and direction angle (θ, ϕ) were robust against these errors compared to those of small ones. Detailed numerical comparison would not be listed here.
2.5. The determination of vector magnetic field directionDue to the mirror symmetry of NV–13C, eight possible combinations of polar angles
 and azimuth angles (ϕ,π±ϕ,2π-ϕ) correspond to nearly identical
and azimuth angles (ϕ,π±ϕ,2π-ϕ) correspond to nearly identical
 and Δ. However, for a definite NV–13C hyperfine tensor, the polar angle θ could be firstly decided by observing relative fluorescence intensity of CW spectrums as shown in Fig. 4(a). More details refer to Appendix C. The eight possible directions could be narrowed down to four ones as illustrated in Fig. 7.
and Δ. However, for a definite NV–13C hyperfine tensor, the polar angle θ could be firstly decided by observing relative fluorescence intensity of CW spectrums as shown in Fig. 4(a). More details refer to Appendix C. The eight possible directions could be narrowed down to four ones as illustrated in Fig. 7.
Finally, we propose a scheme that the authentic one of the four possible magnetic field directions could be singled out by observing their free dynamical evolutions
 of initial states
of initial states
 under the Hamiltonian (2). The initial electron spin state
under the Hamiltonian (2). The initial electron spin state
 could be prepared in
could be prepared in
 and initial 13C nuclear spin state
and initial 13C nuclear spin state
 or
or
 , respectively. Finally,
, respectively. Finally,
 is projected into ground state
is projected into ground state
 with
with
 . The resulting population evolutions p(τ) under different initial 13C nuclear spin state
. The resulting population evolutions p(τ) under different initial 13C nuclear spin state
 could exclude the symmetrical solutions of four azimuth angles ϕ as shown in Fig. 8. The envelopes contain rapid oscillations, which are from the term of zero-field splitting D in the laboratory frame. In experiment, FID signal could be measured.
could exclude the symmetrical solutions of four azimuth angles ϕ as shown in Fig. 8. The envelopes contain rapid oscillations, which are from the term of zero-field splitting D in the laboratory frame. In experiment, FID signal could be measured.