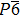† Corresponding author. E-mail:
The compressibility and pressure-induced phase transition of β-Si3N4 were investigated by using an angle dispersive x-ray diffraction technique in a diamond anvil cell at room temperature. Rietveld refinements of the x-ray powder diffraction data verified that the hexagonal structure (with space group P63/m, Z = 2 formulas per unit cell) β-Si3N4 remained stable under high pressure up to 37 GPa. Upon increasing pressure, β-Si3N4 transformed to δ-Si3N4 at about 41 GPa. The initial β-Si3N4 was recovered as the pressure was released to ambient pressure, implying that the observed pressure-induced phase transformation was reversible. The pressure–volume data of β-Si3N4 was fitted by the third-order Birch–Murnaghan equation of state, which yielded a bulk modulus K0 = 273(2) GPa with its pressure derivative 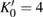
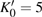
Ceramic silicon nitride (Si3N4) has a broad range of applications (cutting tools, antifriction bearings and etch masks in microelectronics) in various industries because of its superior properties such as excellent mechanical strength, high thermal stability and relatively low mass density.[1–4] Studying the influence of pressure on the structural stability and possible phase transition of β-Si3N4 will provide us with insight into its potential applications under extreme conditions. The two known polymorphs of silicon nitride are α-Si3N4 and β-Si3N4. Both have a hexagonal lattice with different stacking sequences of the layered atoms perpendicular to the c-axis. A third cubic form (c-Si3N4) with a spinel structure has been found recently and studied at pressures above 15 GPa and temperatures over 2000 K.[5–11] This phase, c-Si3N4, is expected to be a hard material. In 2016, Nishiyama et al. reported the synthesis of the hardest transparent spinel ceramic, i.e., polycrystalline cubic silicon nitride (c-Si3N4). It is believed to be the third-hardest material after diamond and cubic boron nitride (cBN).[12–14] So it is of great importance to study the high-pressure behavior of silicon nitride.
In 2001, Zerr et al. found the fourth form of Si3N4 (labeled the δ phase) by energy dispersive x-ray diffraction (EDXD) measurements, which were derived from a pressure-induced phase transition of the β-Si3N4 at 42.6 GPa.[15] However, the obtained data (only one pattern) was not enough to determine the structure of δ-Si3N4.[15] After that, although some people predicted the structure of the δ-Si3N4 (Table 
| Table 1.
The predicted lattice parameters, Wyckoff positions, and space group of δ-Si3N4. . |
| Table 2.
Comparison of compressibility and phase transition pressure: bulk modulus K0, its pressure derivative |
In this work, we investigated the compression behavior of β-Si3N4 at room temperature using ADXRD measurement and determined the equation of state (EOS) of β-Si3N4 under high pressure of up to 37 GPa. The pressure-induced reversible phase transformation process from β-Si3N4 to δ-Si3N4 was observed at ambient temperature.
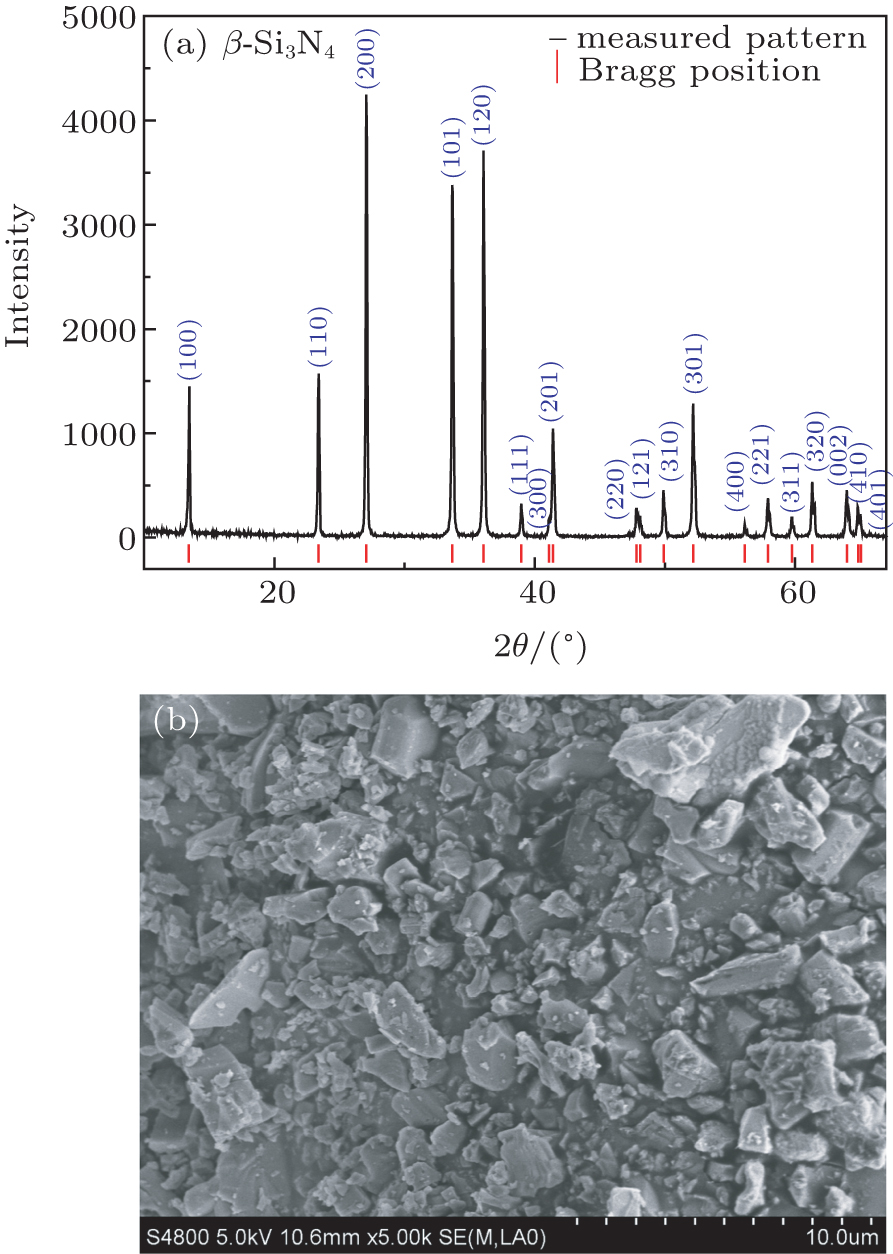
The initial silicon nitride (β-Si3N4) powder (99.9% purity, 
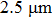
High pressure was generated using a symmetric-type DAC with the culet size of 



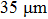
In situ high pressure ADXRD experiments were performed at room temperature at the 4W2 beamline of the Beijing Synchrotron Radiation Facility (BSRF, China), Chinese Academy of Sciences. In all experiments, the synchrotron source with a wavelength of 0.6199 Å was tuned by a Si (111) monochromator. The incident x-ray beam was focused to approximately 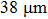

Figure
 | Fig. 2. (color online) Representative high-pressure synchrotron radiation XRD patterns of β-Si3N4 at various pressures. |
 | Fig. 3. Typical two-dimensional ADXRD patterns obtained from β-Si3N4 under different pressures: (a) P = 33.8 GPa, (b) P = 37.0 GPa, (c) P = 41.0 GPa. |
Figure
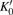

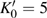
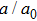
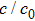
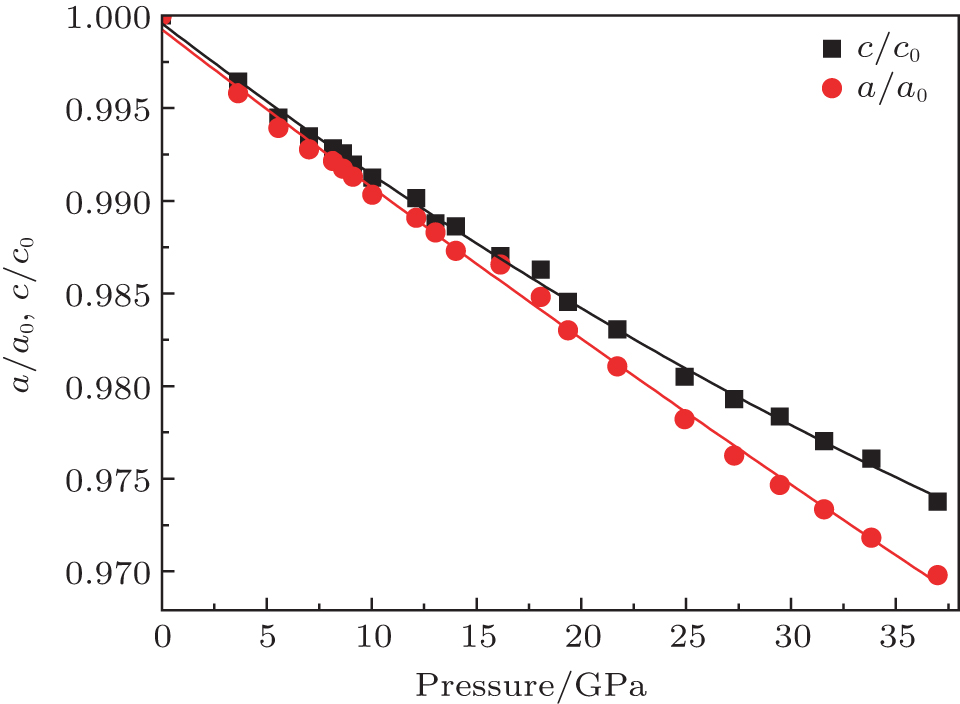 | Fig. 6. (color online) Compressibility of the normalized lattice parameters of β-Si3N4. As the pressure increases the anisotropy of β-Si3N4 becomes more and more distinct. |
 | Fig. 7. (color online) Crystal structure of β-Si3N4. Large blue spheres represent Si atoms and small green spheres are N atoms. |
| Table 3.
Calculated elastic constants Cij (GPa) of β-Si3N4 under pressures up to 35 GPa from Ref. [30]. . |
In summary, the phase transition and compressibility of β-Si3N4 were investigated at pressure up to 45.6 GPa by synchrotron ADXRD at room temperature. A pressure-induced reversible phase transition was observed at 41 GPa. The compression curve of β-Si3N4 yielded a bulk modulus 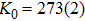



| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] |