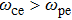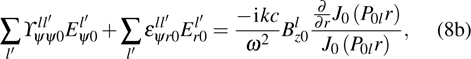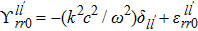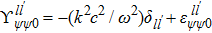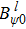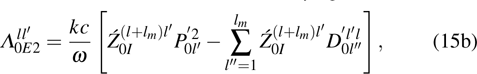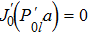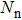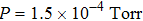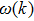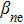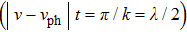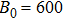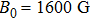1. IntroductionSeveral theoretical and experimental studies have been conducted to describe the guiding mechanism of electromagnetic waves by a plasma waveguide.[1–3] Some important applications can be found in various areas such as high power microwave (HPM) devices,[4,5] industrial plasmas, plasma diagnosis[6] and plasma limiters.[7,8] The latter is used in protective devices against HPM and pulses with very short rising time. The wave–plasma interaction gives rise to different phenomena including absorption, reflection, scattering and transmission of the incident EM wave[9–13] as well as mode excitation, radiation and instability production in plasma.[14–18] Vidmar et al. reported that the plasma layer generated at atmosphere pressure can be used as a broadband absorber.[19] The absorption mechanism in plasma is categorized into collision[20–23] and collisionless[24–26] damping. In the collision mechanism, the wave energy diminishes due to elastic or inelastic collision of the wave with electrons, ions or neutral atoms.
As mentioned above, the wave damping in plasma occurs even in the absence of particle collisions. The collisionless wave damping plays an important role in plasma heating. The Landau and cyclotron damping processes are famous examples of this type of absorption mechanism. Collisionless Landau wave damping has a simple physical concept in plasma. To be more precise, when a unique electron of plasma moves in the electric field of a wave, its energy can be diminished if the electron velocity is larger than the phase velocity of the wave. On the other hand, the electron can receive additional energy from the wave if its velocity is smaller than the phase velocity of the wave. Furthermore, the total energy balance for a swarm of electrons can be attributed to the quantity of “cold” and “warm” electrons. It is worth noting in this context that the quantity of cold electrons is more than that of warm electrons in the Maxwellian distribution. Such a fact can obviously lead to a well-known phenomenon, namely, the collisionless Landau damping of the electric field perturbation.
The ECR absorption in a cylindrical microwave discharge has been investigated through kinetic theory.[27,28] Landau damping[29] was first experimentally observed by calculating the spatial damping length of Trivelpiece–Gould (TG) waves in an open-ended neutral plasma column. In recent years, Landau damping has been studied in plasmas with different distribution functions.[30–34] Liu et al.
[33] derived the generalized dispersion equation for longitudinal oscillation in an unmagnetized, collisionless, isotropic and relativistic plasma in the context of nonextensive q-distribution.
There are two types of processes (linear and nonlinear) in the Landau damping mechanism. Linear Landau damping occurs when the resonant particles in the original distribution have a velocity close to that of the wave phase. On the other hand, when the wave amplitude increases and collisionless damping with trapped particles takes place, nonlinear Landau damping occurs.[35,36] Qureshi et al.
[36] presented theoretical analysis of the nonlinear Landau damping of Langmuir waves in an unmagnetized plasma. The concept of Landau damping is widely used in the phenomena of anomalous plasma losses from fusion devices, ensemble studies of gravitating objects, mechanics of continuous media, in elementary particle physics and many other areas of science.
The theory of nonlinear damping (growth) of Langmuir waves in collisionless inhomogeneous plasma was developed by Karpman et al.
[37] Several important studies have been carried out on the effect of the plasma parameters on Landau damping of plasma waveguides.[38–40] Xu et al.
[38] investigated the effects of ion motion on Landau damping aided by one-dimensional Vlasov–Poisson simulation. It was shown that the ion motion can significantly change the development of linear Landau damping. In another study performed by Rose et al.,[39] the increased Landau damping of electrostatic waves in the presence of low density suprathermal electron populations was examined. Zakeri et al.
[40] studied the dependence of Landau damping on the plasma parameters and the effects of the metallic tube boundary on the dispersion characteristics of four families of modes in a cylindrical homogeneous plasma waveguide.
In the present study, the radial inhomogeneity effect on Landau damping of space-charge and cyclotron waves in a cylindrical plasma waveguide is analyzed by using the Bessel–Furrier expansion for the first time. The Landau damping of the hybrid modes can be neglected due to their very small rate. Since the influence of inhomogeneity and temperature parameters on Landau damping is not equal in different magnetic fields, the diagrams are plotted in two ranges of magnetic field
 and
and
 . The wave equations of the inhomogeneous warm magnetized plasma waveguide and the dispersion relation obtained in the Bessel–Furrier space are presented in Section 2. In Section 3, the reason for neglecting collision damping is analyzed and the Landau damping of electrostatic waves is numerically discussed. Section 4 is devoted to summarizing the main points and findings of this paper.
. The wave equations of the inhomogeneous warm magnetized plasma waveguide and the dispersion relation obtained in the Bessel–Furrier space are presented in Section 2. In Section 3, the reason for neglecting collision damping is analyzed and the Landau damping of electrostatic waves is numerically discussed. Section 4 is devoted to summarizing the main points and findings of this paper.
2. Wave equationsThe geometrical shape of the waveguide is cylindrical with radius a. It is fully filled by an inhomogeneous collisionless plasma (Fig. 1). This structure is exposed to an external steady-state magnetic field
 , where
, where
 is the waveguide axis. In this study, ions are assumed to be stationary, while the thermal motion of electrons is taken into account. In addition, it is assumed that the plasma is nonuniform along the r-axis. Maxwellʼs equations for the magnetized radially inhomogeneous plasma are
is the waveguide axis. In this study, ions are assumed to be stationary, while the thermal motion of electrons is taken into account. In addition, it is assumed that the plasma is nonuniform along the r-axis. Maxwellʼs equations for the magnetized radially inhomogeneous plasma are
Here,
 is the material equation that is given by
is the material equation that is given by
where

is the dielectric tensor of the inhomogeneous plasma with a strong spatial dispersion. In order to obtain an analytical solution of the Maxwell and material equations for the inhomogeneous plasma with strong spatial dispersion, conventional methods such as geometrical optics cannot be used. Therefore, we use the Fourier–Bessel transformation and differential Fourier–Bessel transformation to localize these equations.
[41,42] The localization of the material equation in Fourier–Bessel space is expressed as
In addition, the components of this tensor are obtained through the Vlasov equation in the localized space by Bessel–Fourier expansion. Without loss of generality, from the dielectric tensor of the magnetized inhomogeneous warm plasma,[42] one can find the dielectric tensor of the plasma without density gradient for cyclotron harmonic numbers n = −1,0,1 as
Here
ω is the frequency of the electromagnetic wave,
kz is the longitudinal wave number,

is the plasma frequency and

is the cyclotron frequency. In addition, we have

and

. The thermalvelocity of electrons is

and coefficients

are defined in the Appendix. It should be noted that in the limiting case of cold homogeneous cylindrical magnetoplasma, the cyclotron harmonic number is
n = 1 and

. The term

is the plasma dispersion function tabulated by Fried and Conte
[43]
The plasma is considered to be warm so that factor
 takes an arbitrary value between zero to infinity. Moreover, using the asymptotic definition of
takes an arbitrary value between zero to infinity. Moreover, using the asymptotic definition of
 is not permitted. In order to obtain the wave equations for the electric field in the direction of propagation, we start with Maxwellʼs curl equation. By using the Bessel–Fourier expansion, the Maxwell curl equations in this space for the symmetric mode (m = 0) can be written as[42]
is not permitted. In order to obtain the wave equations for the electric field in the direction of propagation, we start with Maxwellʼs curl equation. By using the Bessel–Fourier expansion, the Maxwell curl equations in this space for the symmetric mode (m = 0) can be written as[42]
where
Using Eq. (
7a) and substituting Eqs. (
6a) and (
6d) with Eqs. (
6e) and (
6b), respectively, we obtain the following equations:
in which

are the radial wave numbers determined by the boundary condition (

, i.e.,

, where

is the
l-th root of

. Moreover, we have
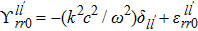
and
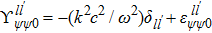
. Consequently, instead of Eqs. (
8a) and (
8b), we are faced with a 2
l equation. These equations in their matrix form are expressed as
The radial and azimuthal components of the electric field can be obtained versus the axial components of the electric and magnetic fields by solving Eq. (9) as follows:
Also, substituting Eqs. (
10a) and (
10b) with Eqs. (
6a) and (
6b), respectively, we obtain the transverse components of the magnetic field as
The parameter

represents the element on row
l and column

of the inverse of the coefficient matrix in Eq. (
9) and
lm is the maximum value of the radial number (
l). Finally, the wave equation of the electric field is obtained by substituting

and
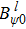
parameters in Eq. (
6f)
where
Furthermore, by using the same method in the derivative Bessel–Furrier space, the wave equation of the magnetic field can be obtained by substituting
 and
and
 in the z-component of the Ampere law as follows
in the z-component of the Ampere law as follows
in which
where

is the radial wave number. It is determined by the boundary condition of
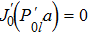
, i.e.,

, where,

is the

-th root of

. Note that

is the element on row
l and column

of the inverse of the coefficient matrix in Eq. (
9) in the derivative Bessel–Fourier space.
The dispersion equations can be written in the following matrix form:
The nontrivial solutions of the above equations are obtained by setting the determinant of the coefficients matrix to zero (the above

matrix).
3. DiscussionThe effective collision frequency from the Krook model is given by[44]
where

and

are the electron–ion and electron–neutral collision frequencies, respectively. The term

is the Coulomb logarithm. On the basis of the Krook model, the electron–neutral particle collision frequency is obtained as

. We assume that the term

is equal to 10 when the electron temperature
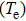
is in the range of a few electron volts. The terms
σ,
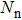
and

are the cross section of the electron scattering, the number of atoms in gas and the thermal velocity of electrons, respectively. The gas pressure of the plasma waveguide in microwave amplifiers and accelerators is in the range of

.
[45] In this paper, with a plasma density of

, pressure
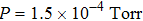
and electron temperature

, we have

and

. In this way, the effective collision frequency is equal to

. Here, we deal with the gigahertz frequency regime (

) and the term

becomes smaller than unity, therefore the plasma is considered collisionless.
Landau damping is a collisionless damping mechanism in plasma. When the thermal motion of plasma particles is not negligible and it is very close to the phase velocity of plasma modes, Landau damping plays a significant role. In warm plasma, an imaginary term appears in the dielectric tensor which leads to the formation of a complex dispersion equation. In other words, the dispersion relation for a real wave number has a complex frequency solution.[46] The solution is in the form of
 , in which
, in which
 is the dispersion equation and
is the dispersion equation and
 is the Landau damping rate for each of the space-charge and cyclotron modes. If the imaginary part of the dispersion equation becomes much smaller than its real part ([
is the Landau damping rate for each of the space-charge and cyclotron modes. If the imaginary part of the dispersion equation becomes much smaller than its real part ([
 , then
, then
 is given by[46]
is given by[46]
where
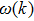
is the root of the real part of the dispersion equation. The imaginary part of the dispersion relation results from the imaginary part of the complex function of

. Note also that this imaginary part is proportional to the term

. Due to the presence of an exponential function in this term, any parameter that decreases (increases)
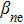
leads to an increase (decrease) in the Landau damping. From the physical aspect, decreasing the phase velocity increases resonance particles which do not have a different velocity in the order of the half wavelength
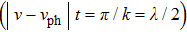
in the Boltzmann–Maxwell function. In the Maxwell–Boltzmann function for domains with a negative derivative, as the phase velocity decreases, the number of resonance particles with smaller velocities than the phase velocity tends to increase (Fig.
2). Such resonance particles are believed to be the main reason for the existence of linear Landau damping. Therefore, the decrease in

or phase velocity leads to an increase in the number of particles with smaller velocities and subsequently the Landau damping.
To better understand the Landau damping, we discuss its frequency. The Landau damping frequency is expressed as[47]
where

. It is noticeable that due to the variations of

with

, two distinct regimes are defined as

and

. The parameter

is a general criterion for investigating the Landau damping intensity. In the regime

, the Landau damping frequency

increases for the lower values of

(i.e.,

tends to unity). It leads to an increase in the power absorption of Landau damping. Although, in the regime

, the Landau damping frequency

increases for higher values of

(i.e.,

tends to unity), the power absorption of the Landau damping also increases in this case. Figure
3 plots the Landau damping frequency with respect to the wave number. According to this figure, increasing the longitudinal wave number leads to an increase in the Landau damping frequency of both modes. Furthermore, the value of

is comparable with the frequency of space-charge and cyclotron modes (in the range of gigahertz). In contrast, for the hybrid modes (

,

),

is very small in any value of
kz and is not comparable with the frequency of these modes. Hence, the Landau damping portion of waveguide modes is not taken into account in this paper and we only investigate the Landau damping of space-charge and cyclotron modes. It is worth noting that, according to Fig.
3, increasing the value of
l increases the

of the space-charge mode and decreases the

of the cyclotron mode. Moreover, it is found that the inhomogeneity effect decreases the Landau damping frequency of the space-charge mode and increases the Landau damping frequency of the cyclotron mode.
In this paper, we also study numerically the Landau damping of a cylindrical waveguide completely filled by magnetized inhomogeneous warm plasma. The azimuthal and cyclotron harmonic numbers of the dielectric tensor are assumed to be m = 0 and n = −1,0,1, respectively. In a warm plasma column, the factor
 takes an arbitrary value between zero to infinity for any plasma parameters. Hence, in order to calculate the Landau damping coefficient, we use the direct definition of the plasma dispersion function
takes an arbitrary value between zero to infinity for any plasma parameters. Hence, in order to calculate the Landau damping coefficient, we use the direct definition of the plasma dispersion function
 in terms of a complex error function[48] instead of its asymptotic definition, which has been conventionally used in previous theoretical works. The waveguide radius and plasma density are taken as[49] a = 1.55 cm and
in terms of a complex error function[48] instead of its asymptotic definition, which has been conventionally used in previous theoretical works. The waveguide radius and plasma density are taken as[49] a = 1.55 cm and
 , respectively. To generalize the discussion about the dispersion equation of a waveguide filled with inhomogeneous and magnetized plasma, the analysis is performed for two limits
, respectively. To generalize the discussion about the dispersion equation of a waveguide filled with inhomogeneous and magnetized plasma, the analysis is performed for two limits
 and
and
 . Based on Malbergʼs experimental research,[50] the inhomogeneous density profile is considered as
. Based on Malbergʼs experimental research,[50] the inhomogeneous density profile is considered as
 . All frequencies and wave numbers are normalized by
. All frequencies and wave numbers are normalized by
 and
and
 , respectively. The coefficient c represents the velocity of the light.
, respectively. The coefficient c represents the velocity of the light.
In order to analyze the effect of the plasma parameter on Landau damping, the discussion is divided into three subsections. In Subsection 3.1, the effect of inhomogeneity on Landau damping is studied. Subsection 3.2 focuses on the investigation of electron thermal motion effects on Landau damping. Finally, the effect of the magnetic field on Landau damping is discussed in Subsection 3.3.
3.1. Effect of inhomogeneity on Landau dampingThe logarithmic plots of Landau damping in terms of wave number are shown in Figs. 4 and 5 for cyclotron and space-charge modes in two limits of
 and
and
 . The graphs have been plotted for three different inhomogeneity parameters. In these figures, the solid line corresponds to the case of homogenous warm plasma with
. The graphs have been plotted for three different inhomogeneity parameters. In these figures, the solid line corresponds to the case of homogenous warm plasma with
 , while the dashed and dashed-dotted lines refer to the inhomogeneous warm plasma cases with
, while the dashed and dashed-dotted lines refer to the inhomogeneous warm plasma cases with
 and
and
 , respectively. Panels (a) and (c) correspond to l = 1, while panels (b) and (d) correspond to l = 4. Note also that the top and bottom panels have been plotted for magnetic field
, respectively. Panels (a) and (c) correspond to l = 1, while panels (b) and (d) correspond to l = 4. Note also that the top and bottom panels have been plotted for magnetic field
 G and 1800 G, respectively.
G and 1800 G, respectively.
From Fig. 4, it can be concluded that:
(I) The inhomogeneity parameter increases the Landau damping of the cyclotron modes.
(II) The increasing rate of Landau damping due to the inhomogeneity effects decreases as the magnetic field rises.
(III) For larger values of l, the effect of inhomogeneity on Landau damping becomes less significant in analogy to the smaller values of l.
Generally, the Landau damping has an inverse relation with the term
 . In other words, each plasma parameter which decreases (increases) the term
. In other words, each plasma parameter which decreases (increases) the term
 leads to an increase (a decrease) in Landau damping. For instance, the inhomogeneity parameter decreases the term
leads to an increase (a decrease) in Landau damping. For instance, the inhomogeneity parameter decreases the term
 , therefore it increases the Landau damping. On the other hand, stronger magnetic fields and larger values of l (that increase the term
, therefore it increases the Landau damping. On the other hand, stronger magnetic fields and larger values of l (that increase the term
 reduce the Landau damping.
reduce the Landau damping.
In contrast to the cyclotron mode, the inhomogeneity effect on Landau damping for the space-charge mode is much more complicated (Fig. 5). In fact, as the wave number increases, the general behavior of the inhomogeneity effect on Landau damping in space-charge mode gradually varies. For given plasma density, magnetic field and thermal motion, there is a wave number for which the effect of inhomogeneity on Landau damping of space-charge mode changes drastically from the positive effect to negative one. We define this point as the turning point of the inhomogeneity effect on space-charge mode. This point is actually the result of two different effects of inhomogeneity on the space-charge mode. The first effect is related to the decrease of the phase velocity. To be more precise, as can be seen in Fig. 6, such a decrease in the phase velocity leads also to a decrease in the term
 and consequently an increase in the corresponding Landau damping. The second effect occurs when the frequency of the space-charge mode gets away from the cyclotron frequency due to the inhomogeneity effect (line
and consequently an increase in the corresponding Landau damping. The second effect occurs when the frequency of the space-charge mode gets away from the cyclotron frequency due to the inhomogeneity effect (line
 in Fig. 6). It causes an increase of the
in Fig. 6). It causes an increase of the
 and consequently, reduces the Landau damping. In general, if
and consequently, reduces the Landau damping. In general, if
 , the inhomogeneity effect on Landau damping of the space-charge mode is augmented. It is reversed for the range
, the inhomogeneity effect on Landau damping of the space-charge mode is augmented. It is reversed for the range
 . The first effect is the same for both space-charge and cyclotron modes while the second one is entirely different for the two modes. We will explain this point more clearly in the remainder of this section. This argumentation describes all three points observed in Fig. 5, as stated below.
. The first effect is the same for both space-charge and cyclotron modes while the second one is entirely different for the two modes. We will explain this point more clearly in the remainder of this section. This argumentation describes all three points observed in Fig. 5, as stated below.
(I) For the space-charge mode, as the inhomogeneity parameter increases, the Landau damping is also increased in the limit of smaller wave number, while it is decreased in larger wave number limits. From the dispersion diagram (Fig. 6), by increasing the longitudinal wave number, the frequency of the space-charge mode approaches the asymptotic limit of cyclotron frequency
 . As a result, for smaller wave numbers, we have
. As a result, for smaller wave numbers, we have
 , while for larger wave numbers, the relation
, while for larger wave numbers, the relation
 is satisfied. Considering the important remarks about
is satisfied. Considering the important remarks about
 terms, we find that the inhomogeneity parameter increases the Landau damping in smaller wave numbers and decreases it in larger ones.
terms, we find that the inhomogeneity parameter increases the Landau damping in smaller wave numbers and decreases it in larger ones.
(II) As the magnetic field is amplified, the inhomogeneity effect on Landau damping of the space-charge mode becomes more significant (Fig. 5). The parameter
 increases as the magnetic field increases. Thus, it would satisfy the
increases as the magnetic field increases. Thus, it would satisfy the
 condition for larger
condition for larger
 intervals. Hence, the turning point of Landau damping is shifted to larger wave numbers.
intervals. Hence, the turning point of Landau damping is shifted to larger wave numbers.
(III) The turning point of Landau damping shifts to smaller kz as the l number increases (Fig. 5). As has been shown in Figs. 6(a) and 6(b), the frequency of the space-charge mode follows an increasing trend with wave number for larger l numbers. Consequently, this frequency approaches to the asymptotic limit in lower kz. In other words, in smaller wave numbers, the inequality
 will be satisfied, so that it can lead to a decrease in Landau damping due to the inhomogeneity effect.
will be satisfied, so that it can lead to a decrease in Landau damping due to the inhomogeneity effect.
As mentioned above, for the cyclotron mode, the effect of inhomogeneity on
 is different from that for the space-charge mode. Actually, due to the decreasing behavior of the dispersion relation in the cyclotron mode, the inhomogeneity effect reduces
is different from that for the space-charge mode. Actually, due to the decreasing behavior of the dispersion relation in the cyclotron mode, the inhomogeneity effect reduces
 (Figs. 6(c) and 6(d)). As we noted earlier, the reduction of
(Figs. 6(c) and 6(d)). As we noted earlier, the reduction of
 increases the Landau damping of the cyclotron mode. Therefore, the variations of both
increases the Landau damping of the cyclotron mode. Therefore, the variations of both
 and
and
 lead to an increase of the Landau damping. Hence, we do not observe any turning point in the case of the cyclotron mode (Fig. 4). We can also conclude from Fig. 4 that the effect of inhomogeneity on the Landau damping of the cyclotron mode is less significant for higher magnetic fields.
lead to an increase of the Landau damping. Hence, we do not observe any turning point in the case of the cyclotron mode (Fig. 4). We can also conclude from Fig. 4 that the effect of inhomogeneity on the Landau damping of the cyclotron mode is less significant for higher magnetic fields.
3.2. Effect of thermal motion on Landau dampingAs can be seen in the dispersion relation curves shown in Figs. 7 and 8, the effect of thermal motion increases smoothly the frequency of the space-charge and cyclotron modes. In fact, the frequency of both modes is a smooth function of temperature. On the other hand, note that the denominator of
 includes
includes
 . In fact, although any increase in the frequency can lead to an increase of
. In fact, although any increase in the frequency can lead to an increase of
 , it is much less than the reduction of
, it is much less than the reduction of
 due to the increasing of
due to the increasing of
 . Consequently, the thermal motion decreases
. Consequently, the thermal motion decreases
 in total and leads to an increase in the Landau damping of both modes for any given magnetic field (Figs. 9 and 10).
in total and leads to an increase in the Landau damping of both modes for any given magnetic field (Figs. 9 and 10).
Figures 9 and 10 present the logarithmic Landau damping diagrams of cyclotron and space-charge modes, respectively, for three different temperatures
 , 2 eV, 6 eV at two limits
, 2 eV, 6 eV at two limits
 (
(
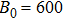 G) and
G) and
 (
(
 G). Note that the plasma is considered to be homogeneous for all cases. According to Fig. 99, it can be concluded that the influence of thermal motion on Landau damping is more significant at
G). Note that the plasma is considered to be homogeneous for all cases. According to Fig. 99, it can be concluded that the influence of thermal motion on Landau damping is more significant at
 . In other words, increasing the magnetic field leads to a decrease in the thermal motion effect on Landau damping in cyclotron mode. However, according to Fig. 1010, we have a different situation for the case of space-charge mode. Actually, the effect of thermal motion on the increasing of Landau damping is absolutely more considerable at
. In other words, increasing the magnetic field leads to a decrease in the thermal motion effect on Landau damping in cyclotron mode. However, according to Fig. 1010, we have a different situation for the case of space-charge mode. Actually, the effect of thermal motion on the increasing of Landau damping is absolutely more considerable at
 (higher magnetic fields). In addition, it can be concluded from Figs. 9 and 10 that by increasing the l number, the effect of thermal motion on increasing the Landau damping of the cyclotron mode is augmented, while it has different effect for the space-charge mode.
(higher magnetic fields). In addition, it can be concluded from Figs. 9 and 10 that by increasing the l number, the effect of thermal motion on increasing the Landau damping of the cyclotron mode is augmented, while it has different effect for the space-charge mode.
3.3. Effect of magnetic field on Landau dampingIn order to analyze the effect of the magnetic field on Landau damping of space-charge and cyclotron modes, the frequency and logarithmic Landau damping versus normalized cyclotron frequency are plotted in the top and bottom panels of Fig. 11, respectively. As can be seen in Fig. 11(c), by increasing the magnetic field, the Landau damping of the cyclotron mode is increased while the opposite effect has occurred for the space-charge mode in Fig. 11(d). The main reasons for this phenomenon are shown in Figs. 11(a) and 11(b), which correspond to the cyclotron and space-charge modes, respectively. Here, by increasing the magnetic field, the frequency of both modes is increased. But, it should be noted that, for the space-charge mode, the frequency increases at first and then approaches to a steady state for a certain cyclotron frequency. In other words, the frequency curve for the cyclotron mode is a fast function of the magnetic field, while for the space-charge mode, it is rather mild. Hence, for the cyclotron mode, the difference between ω and
 is decreased. This fact consequently decreases
is decreased. This fact consequently decreases
 . As mentioned before, decreasing
. As mentioned before, decreasing
 leads to an increase in Landau damping. Note that a contrary effect occurs for the case of the space-charge mode. In addition, it is found that the increasing l number leads to a decrease in the magnetic field effect on the Landau damping for both modes.
leads to an increase in Landau damping. Note that a contrary effect occurs for the case of the space-charge mode. In addition, it is found that the increasing l number leads to a decrease in the magnetic field effect on the Landau damping for both modes.