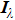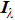† Corresponding author. E-mail:
This paper presents a numerical study on the simultaneous reconstruction of temperature and volume fraction fields of soot and metal-oxide nanoparticles in an axisymmetric nanofluid fuel sooting flame based on the radiative energy images captured by a charge-coupled device (CCD) camera. The least squares QR decomposition method was introduced to deal with the reconstruction inverse problem. The effects of ray numbers and measurement errors on the reconstruction accuracy were investigated. It was found that the reconstruction accuracies for volume fraction fields of soot and metal-oxide nanoparticles were easily affected by the measurement errors for radiation intensity, whereas only the metal-oxide volume fraction field reconstruction was more sensitive to the measurement error for the volume fraction ratio of metal-oxide nanoparticles to soot. The results show that the temperature, soot volume fraction, and metal-oxide nanoparticles volume fraction fields can be simultaneously and accurately retrieved for exact and noisy data using a single CCD camera.
As hydrocarbon fuel supplies are gradually diminishing and environmental pollution is getting worse, the need for new alternatives to conventional hydrocarbon fuels is increasingly imperative. Furthermore, the development of hypersonic vehicle propulsion systems and power microelectromechanical systems are largely dependent on the physical and thermal properties of liquid fuels. Nanofluid fuels are uniform and stable suspensions containing available nanoscale additives in dilute concentrations (
Sabourin et al.[7] compared the combustion of the monopropellant nitromethane with that of nitromethane containing colloidal particles of functionalized graphene sheets or metal hydroxides at room temperature and high-pressure conditions in a silica glass tube. The results demonstrate that the ignition temperature decreases and the burning rates increase for the suspensions compared to those of the monopropellant alone, especially in the burning rate improvement of greater than 175% for graphene sheet suspension. Gan et al.[17,18] investigated the burning characteristics of fuel droplets containing nanosized aluminum, boron, and iron particles, and they proposed various combustion stages (preheating, ignition, classical combustion, microexplosion, surfactant flame, and particle droplet combustion) through observing the recorded burning images of the nanofluid fuel droplets. Tanvir et al.[19] utilized a droplet stream flame to measure the burning rate of ethanol droplets with the addition of graphite nanoparticles, which was determined by estimating droplet sizes at corresponding locations via backlight shadowgraphy using a high-speed camera. Liu et al.[20] analyzed the geometrical parameters of nanofluid fuel flames using an image processing technique to study the combustion characteristics of flowing nanofluid fuels in a half-opening slot tube.
To date, studies on the combustion characteristics of nanofluid fuels are still in the primary stage and the combustion diagnostic methods for nanofluid fuels remain very limited. Temperature, volume fraction fields of soot, and metal-oxide nanoparticles in nanofluid fuel flame are important combustion characteristic parameters and should be measured accurately in the burning process of nanofluid fuel for the in-depth study.
The temperature and particle volume fraction measurement methods of the participating media are categorized as contact and noncontact diagnostic methods. The thermocouple method is one of the most common contact methods. Gan et al.[17] used a type-K thermocouple to suspend the nanofluid fuel droplet and measure its temperature history during the burning process. However, the nanoparticles in the droplet flame easily aggregate and deposit on the thermocouple surface, which decreases the accuracy and sensitivity of temperature measurement. Additionally, only the temperature of the single point in contact with the thermocouple tip can be measured.
Optical measurement techniques are currently preferred for their noncontact and multidimensional measurement advantages, which include tomography reconstruction, light extinction/scattering, and laser-induced incandescence (LII). Because a high-quality background radiation source is needed for transmission measurements, self-emission tomography systems have received particular attention in the last decade. The inverse analysis of radiative heat transfer based on a self-emission tomography system can be used to reconstruct the temperature, soot volume fraction, and radiation property fields of flame from the knowledge of the exit radiation intensity at the boundary surfaces. These days, the optical diagnostic technology combined with inverse radiation analysis for retrieving combustion characteristic fields of flame is developing fast and intensively.[21–43] Zhou et al.[21] first simulated the three-dimensional (3D) temperature distributions in furnaces through radiative energy images captured by multiple charge-coupled device (CCD) cameras mounted around the furnace. They proposed a fast algorithm based on the Monte Carlo method and angular factor effective of image formation to calculate the radiative energy, and used a modified Tikhonov regularization method to solve the inversion problem of 3D temperature distributions. Brisley et al.[23] and Lu et al.[25] applied an imaging-based multicolor pyrometric system combined with a novel optical splitting/filtering device to visualize temperature distributions in a coal-fired flame. Liu et al.[32] developed an inverse radiation analysis based on backward Monte Carlo (BMC) methods and the least squares QR (LSQR) algorithm for concurrent reconstruction of a temperature field and radiative properties in a two-dimensional (2D) rectangular, absorbing, emitting, and scattering gray medium by means of CCD cameras. Subsequently, Liu et al.[33,34] utilized multiple CCD cameras to retrieve the soot temperature and volume fraction profiles in a 3D optically thin flame. Niu et al.[38,39] developed hybrid LSQR-particle swarm optimization (LSQR-PSO) and LSQR-stochastic particle swarm optimization (LSQR-SPSO) algorithms to simultaneously reconstruct 3D temperature distribution and radiative properties of participating media. They found that the temperature field could be estimated to be more accurate than the absorption coefficients and the reconstruction accuracy of temperature distributions, scattering coefficients, and absorption coefficients decrease with the increase in extinction coefficient, but varies little with the scattering albedo. Ni et al.[40] used four CCD cameras combined with liquid crystal tunable filters (LCTF) to capture multispectral flame images for obtaining the line-of-sight radiation intensities, from which temperature and soot volume fraction profiles could be determined. The results show that the average error of the reconstructed volume fraction can be decreased from 8% by a two-color method to 3.17% through a multiwavelength method. Xu et al.[43] proposed a novel optical sectioning tomography for the measurement of 3D temperature of a flame through a single camera in combination with an ionic electrowetting-based variable-focus liquid lens.
The optical reconstruction methods mentioned above only focused on soot-involved flames, but the method for nanofluid fuel flame, in which metal-oxide nanoparticles and soot simultaneously exist, was insufficient. Niu et al.[44] and Huang et al.[45] developed a generalized sourced multiflux method (GSMFM) to simulate outgoing radiation intensities in arbitrary directions for describing the direct problem and used hybrid algorithms to reconstruct 3D temperature distribution and radiative properties in Al2O3 nanoparticle-filled ethylene diffusion flame. However, the retrieved estimations were the corresponding average values in the discrete element of the participating media, and the characteristic parameters for soot and metal-oxide nanoparticles were not distinguished reasonably. In order to further study nanofluid fuel flame, the characteristic parameters fields of metal-oxide nanoparticles and soot required to be respectively constructed.
In the present study, we develop a method for the simultaneous reconstruction of temperature and volume fraction fields of soot and metal-oxide nanoparticles in an axisymmetric nanofluid fuel sooting flame based on the radiative energy images captured by a single CCD camera. The CCD camera can instantaneously capture the images of the entire flame surface from which the radiative intensities can be obtained to overcome the difficulties in measuring the transient spectra of the entire flame by the spectrometer.
The contents of the paper are organized in the following way. The details of direct and inverse problems are described in Section
The direct problem here was to calculate the exit line-of-sight radiation intensity emission based on the known temperature, soot volume fraction, and metal-oxide nanoparticle volume fraction fields in an axisymmetric nanofluid fuel sooting flame.
The considered system based on line-of-sight method is depicted in Fig. 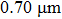
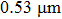

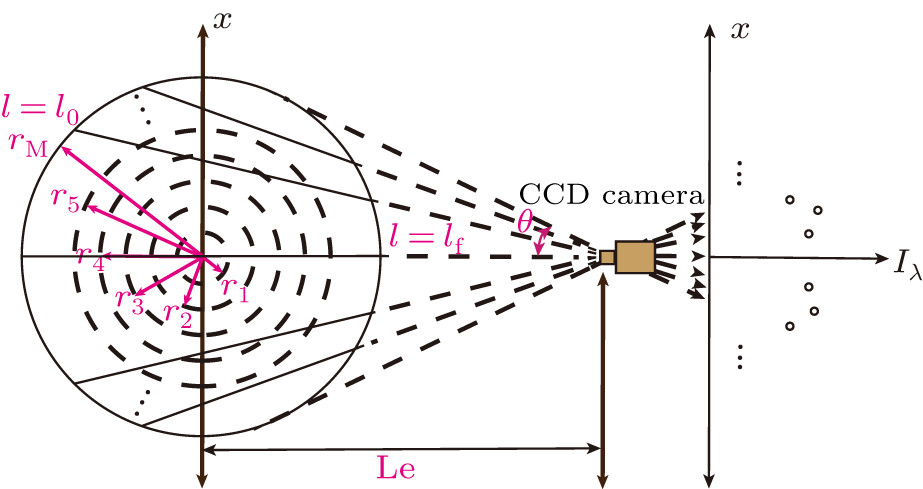 | Fig. 1. (color online) Schematic of line-of-sight radiation intensities received by a CCD camera at a cross-section of a nanofluid fuel sooting flame. |
The nanofluid fuel flame was assumed to be optically thin and the sizes of soot and metal-oxide nanoparticles in the flame were considered to be small in the Rayleigh scattering range. Therefore, the effects of flame species internal self-absorption and scattering can be negligible. The temperature fields of soot and metal-oxide nanoparticles here were considered to be equal and the particle system was independent scattering. Therefore, the following equation can be applied to the radiation intensity emission along ray j from the flame to the CCD camera,
 |

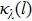
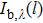

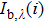

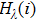


According to Wienʼs law
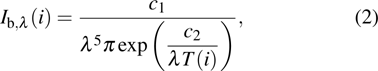 |

The local monochromatic absorption coefficient 
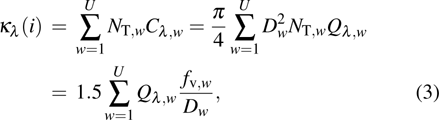 |
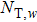

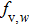


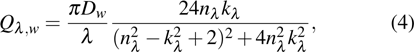 |

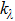
Substituting Eq. (
 |
Equation (
 |
 |

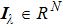
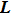



The monochromatic emission source 

For the inverse problem, the temperature, volume fraction fields of soot, and metal-oxide nanoparticles were assumed to be unknown. These parameters can be estimated by the exit line-of-sight radiation intensity vector 
Here, the LSQR algorithm was introduced for solving Eq. (


 |
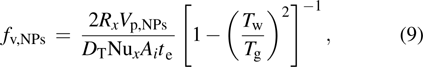 |


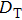
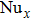
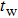


According to Eqs. (
 |
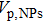

After 
 |
 |
 |
The inverse procedure for retrieving temperature and volume fraction distributions of soot and metal-oxide nanoparticles using a single CCD camera can be summarized as follows.

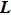




The radiation intensities vectors 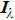
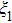

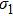
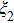
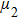
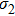
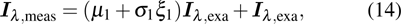 |
 |




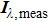
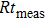
 |
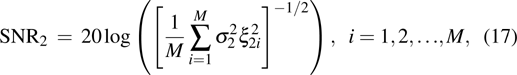 |
To demonstrate the validity and robustness of the reconstruction method, the distributions of temperature and soot volume fraction based on the laminar ethylene diffusion flame at 30 mm in Ref. [20] and the metal-oxide nanoparticles volume fraction distribution estimated from the diffusion flame of ethanol-based fuel with the addition of Al2O3 nanoparticles at 0.05 wt% concentration were adopted in the following simulation research. The flame radius at the given height was set as 3 mm and the horizontal cross-section was evenly divided into 30 rings with equal spacing of 0.1 mm. Figure
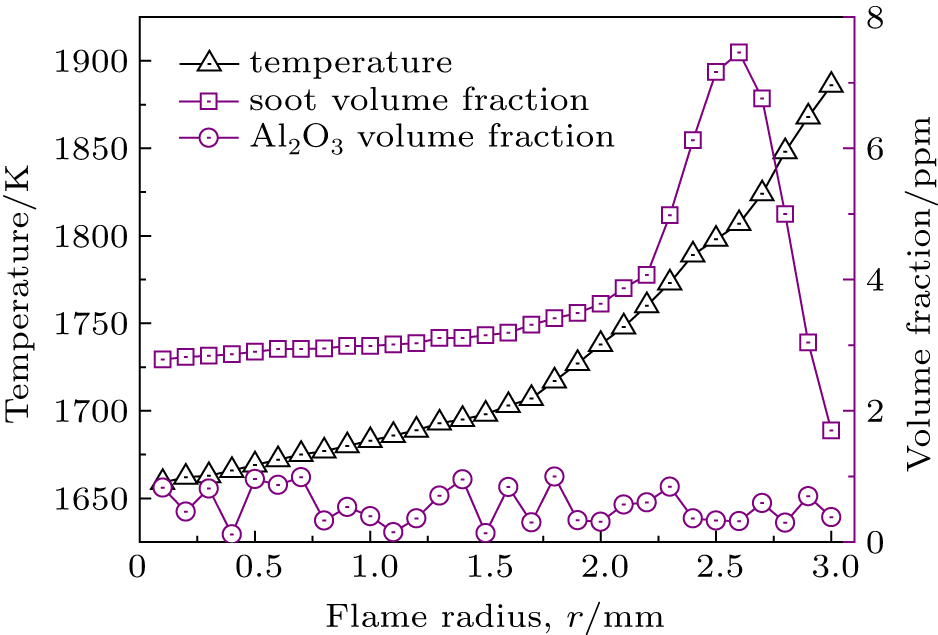 | Fig. 2. (color online) Exact temperature, Al2O3 nanoparticles volume fraction, and soot volume fraction fields. |
The relative errors for temperature (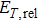


 |
 |
 |
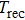


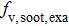


In the following three cases, the effects of ray number, measurement errors of radiation intensity 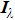
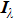

In this case, the effects of ray number and measurement errors for radiation intensity 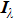
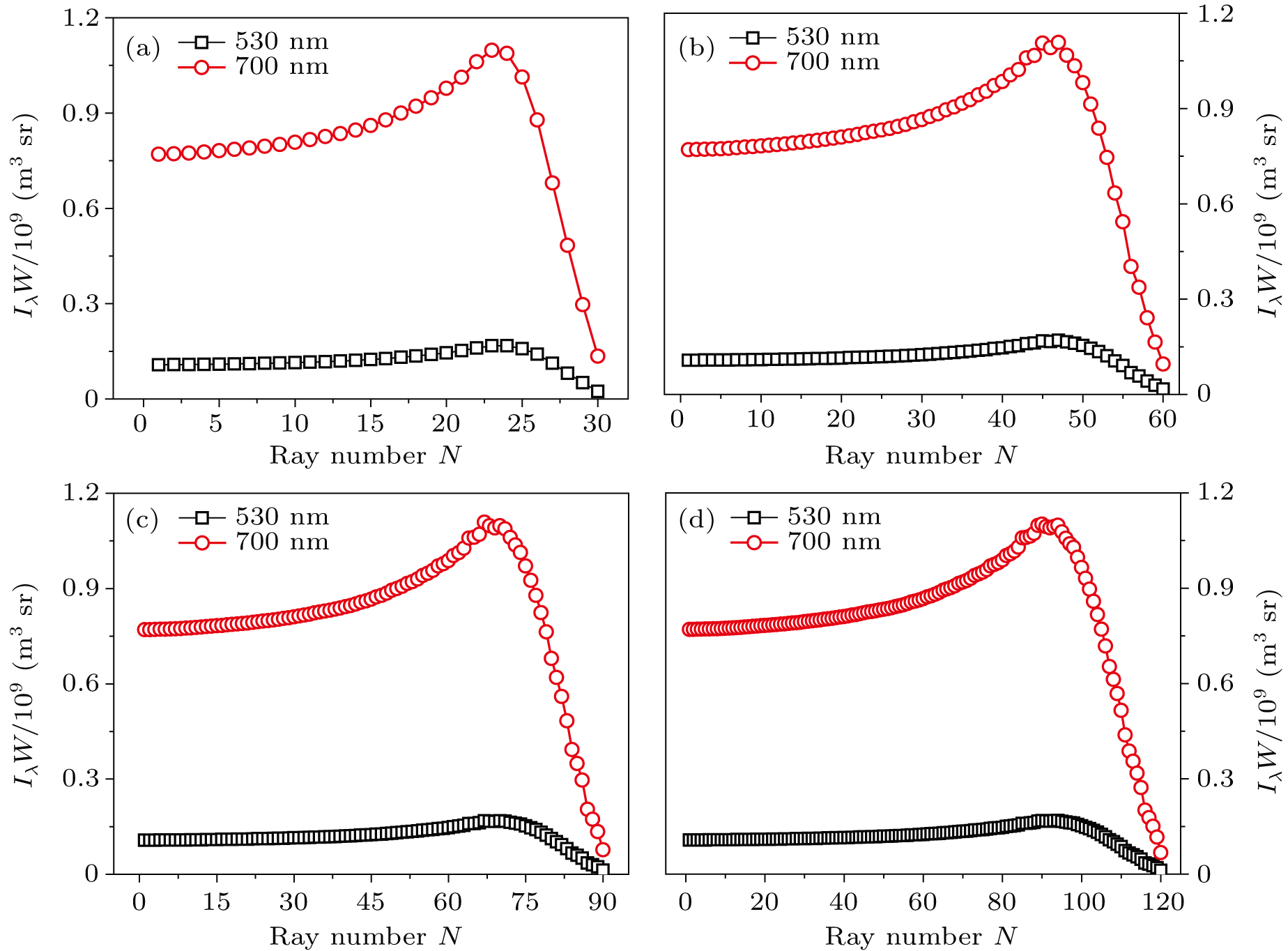
The monochromatic radiation intensity emission profiles of the flame at the red channel (700 nm) and green channel (530 nm) using four ray numbers N (30, 60, 90, and 120) are presented in Fig. 
Here, ray number 90 was used and four different SNR1 were assumed. Owing to the random errors adding to the exact solution of the direct problem, the stability of the reconstruction method was tested through 20 samples, as shown in Fig.
In this case, the effects of measurement errors for the volume fraction ratio
The average of the local relative errors of temperature, soot volume fraction, and Al2O3 volume fraction reconstruction of 20 samples are shown in Fig.
 | Fig. 7. (color online) Effects of measurement errors for volume fraction ratio |
From Fig.
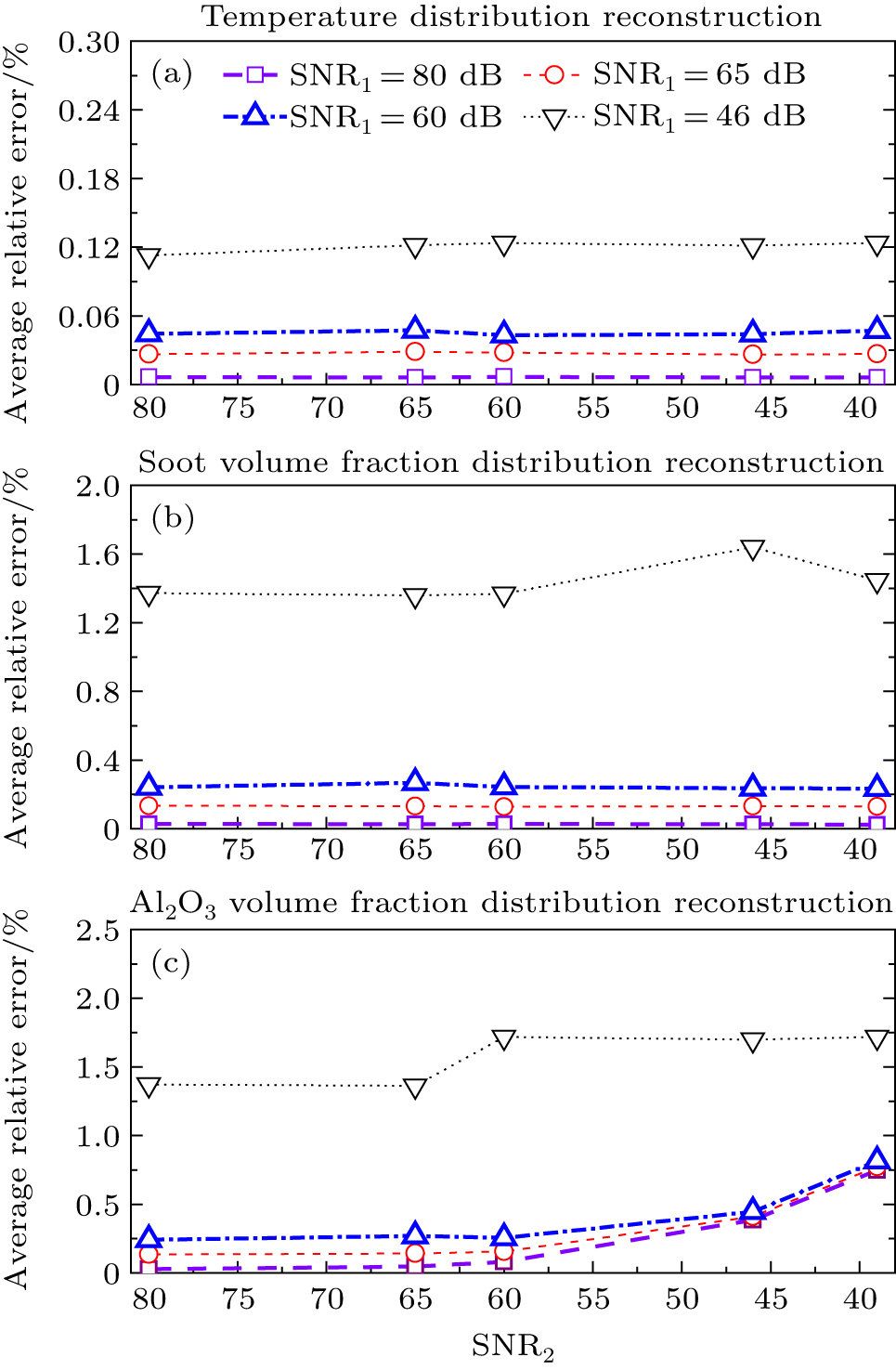
In this case, the measurement errors in the simultaneous presence of radiation intensity 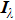
In comparison to the measurement error for the volume fraction ratio 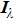
The reconstruction accuracies of the temperature and soot volume fraction distributions were not sensitive to the measurement error for the volume fraction ratio
When SNR1 = 46 dB and SNR2 = 39 dB, the average relative error of the temperature distribution reconstruction was only 0.12%, and that of the volume fraction distribution reconstruction of soot and Al2O3 were only approximately 1.45% and 1.72%, respectively. Therefore, the reconstruction method developed in this study was effective and robust, and could reasonably retrieve the temperature and volume fraction fields of soot and metal-oxide nanoparticles in an axisymmetric nanofluid fuel sooting flame.
An efficient numerical inverse radiation analysis was proposed to reconstruct the temperature and volume fraction fields of soot and metal-oxide nanoparticles in an axisymmetric nanofluid fuel sooting flame using a single CCD camera. Numerical simulations were used and the reconstructed results were acceptable, even in the presence of simultaneous measurement errors of SNR1 of radiation intensity 
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] |