† Corresponding author. E-mail:
An optical method of generating narrowband Lamb waves is presented. It is carried out with a laser line array in a thermoelastic regime implemented by the Michelson interference technique, where the formed array element spacing can be flexibly and conveniently changed to achieve selective mode excitation. In order to simulate the displacement response generated by this array, its intensity distribution function is presented to build a theoretical analysis model and to derive the integral representation of the displacement response. The experimental device and measuring system are built to generate and detect the Lamb waves on a steel plate. Numerical calculation results of narrowband Lamb wave displacement signals based on the theoretical model show good agreement with experimental results.
Guided waves are widely used in industrial inspection tasks due to their unique characteristics suitable for large area and long distance testing.[1–3] However, due to their nature of dispersion and multi-modes, Lamb wave signals are often very complicated, which makes them hard to be utilized. Selective generation methods, such as the comb transducer[4–6] and the angular beam transducer,[7,8] can generate the narrowband and single mode Lamb waves. But these methods need a coupler, which is not suitable in some hostile environments. In those cases, the laser-generated guided wave has become increasingly popular in nondestructive testing (NDT).[9,10] Lamb wave signal generated by pulsed laser is of broadband and multi-mode. In order to excite a narrowband and single mode Lamb wave, some comb transducer-like techniques have been proposed to produce laser line arrays. The current and popular methods proposed for laser line array generation use lenticular arrays[11,12] and the slit mask technique.[13–15] The lenticular array or slit mask technique is relatively easy and effective to implement, but the element spacing is fixed and the very small spacing may be not technically feasible due to the limitation of manufacturing method, which may restrict the applications of these methods. In this paper, we propose to use Michelson interference technique to produce the laser line array in which its element spacing is variable. A beam splitter and two good quality plane mirrors are used to build up this device and the different array element spacings can be produced by only changing the angle between two mirrors. The advantage of this technique is that the element spacing can be flexibly adjusted to achieve the selective Lamb wave mode excitation.
In order to study and implement this kind of laser line array excitation, the properties of the intensity distribution for original laser beam and array generated by Michelson interference fringe are analyzed. The theoretical analysis for the displacement field excited by this array is conducted to simulate guided wave mode generation. An experimental device and a measuring system are built to implement the generation and detection of the narrowband Lamb wave on a steel plate. Numerical calculation based on the theoretical model is carried out and the results are confirmed by experimental results.
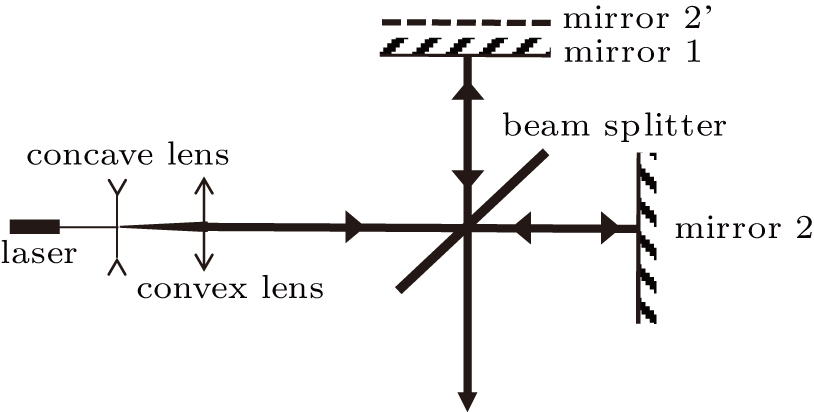
A schematic diagram of the Michelson interference device is shown in Fig.
 |
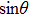
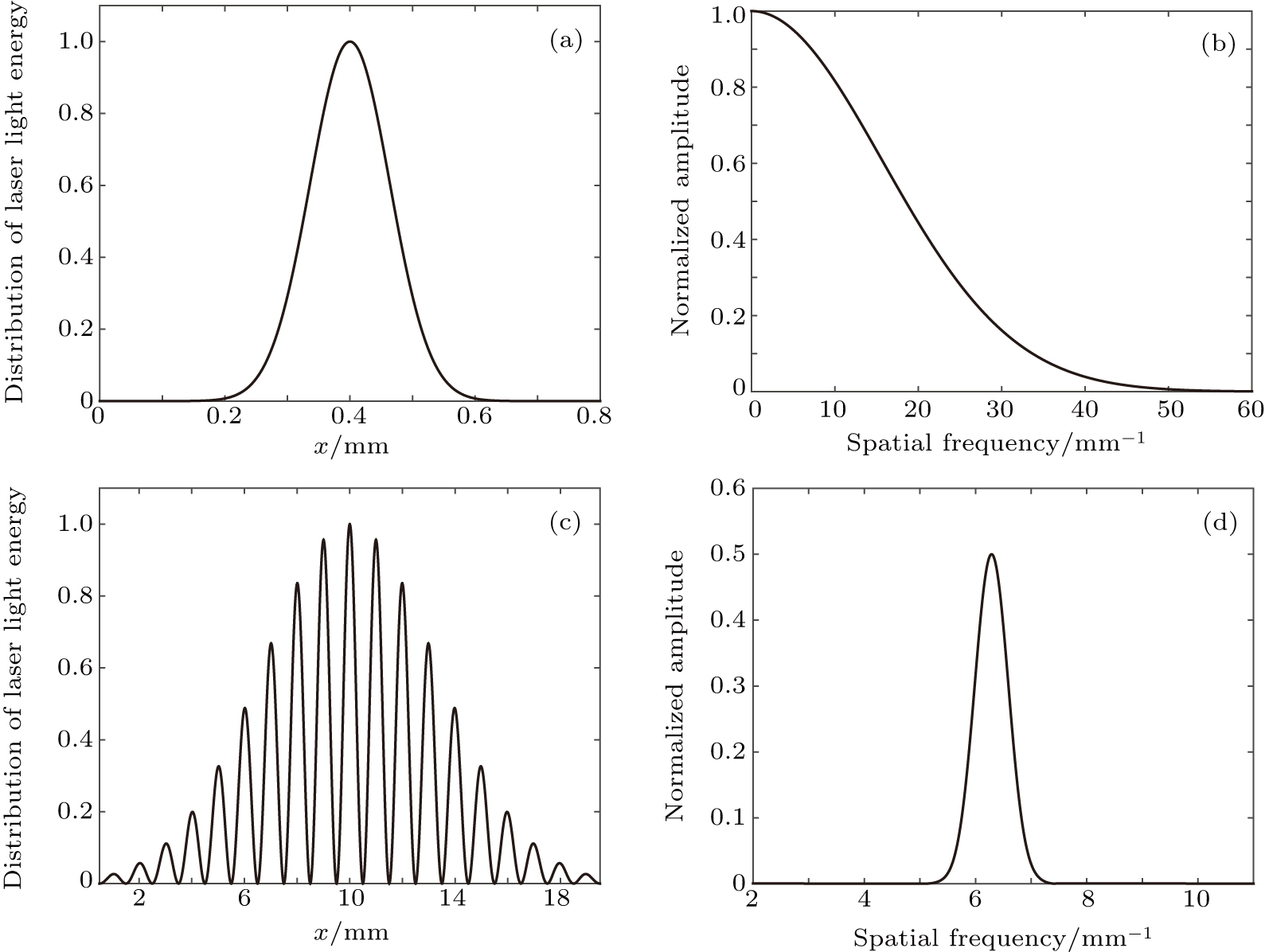
The laser array generated by the Michelson interference technique is nonuniform, and the central lines are stronger than the outer lines due to the Gaussian spatial intensity distribution of the original laser beam. This distribution can be approximately expressed as[12]
 |
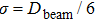
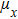
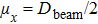
Based on the interference principle,[16] the intensity distribution of interference caused by two coherent and equal irradiant beams is often considered as the 
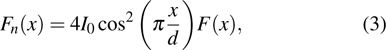 |
The narrowband signals generated by a laser line array produced by The Michelson interference technique can be characterized as the spatial modulation method. For a single line source, its spatial bandwidth is broadband. But a periodically spaced line array can function as a transversal filter, which will effectively reduce the spatial bandwidth. Assuming that a laser line source has an intensity of Gaussian distribution with a full width at half maximum (FWHM) of 0.15 mm as shown in Fig.
Considering a homogenous and isotropic plate, its thickness is 2h. The laser line array in the thermoelastic regime impacts at the upper surface of the plate. The model used in this section is shown in Fig.
The displacement vector 
 |
 |
For a laser array source in thermoelastic regime mentioned above, the boundary conditions of two surfaces for a plate can be given as
 |
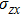



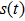
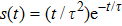

For an isotropic plate, the solutions of the potentials in the frequency–wavenumber 
 |
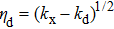
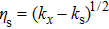

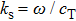
The boundary conditions in the frequency–wavenumber 
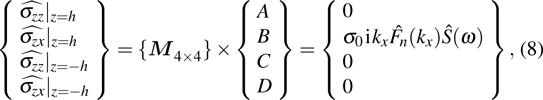 |
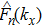

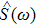
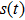
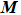
 |
According to Eq. (
 |
By applying Fourier transform to Eq. (
 |
Using Cramerʼs rule, the coefficients A, B, C, D in Eq. (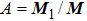


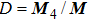
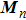



The residue theorem is used to calculate the integral with respect to kx in Eq. (
 |
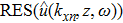
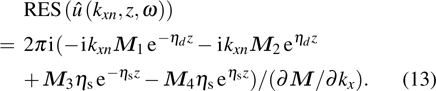 |
| Table 1.
Parameters of the steel materials. . |
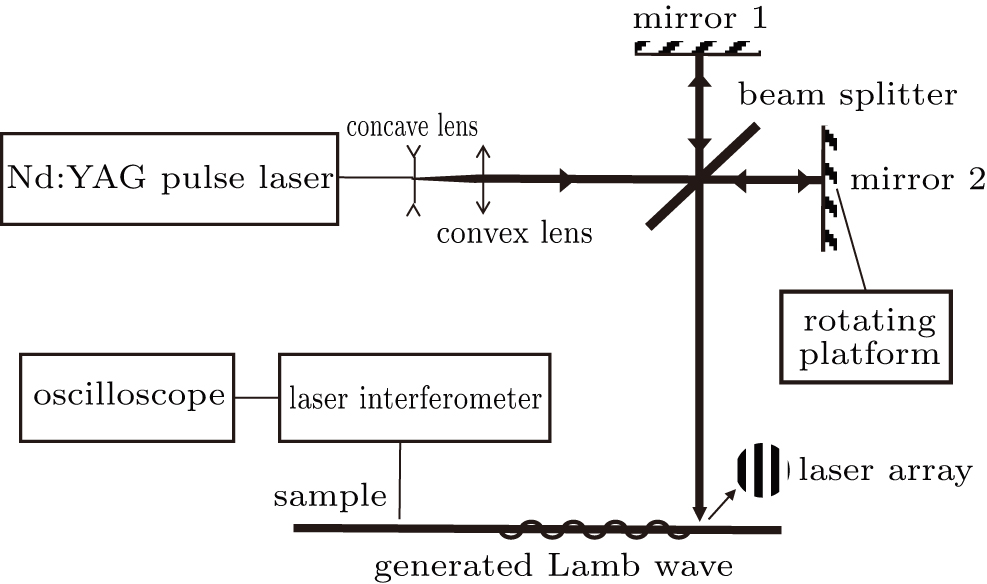
A schematic diagram of the experimental setup is shown in Fig. 
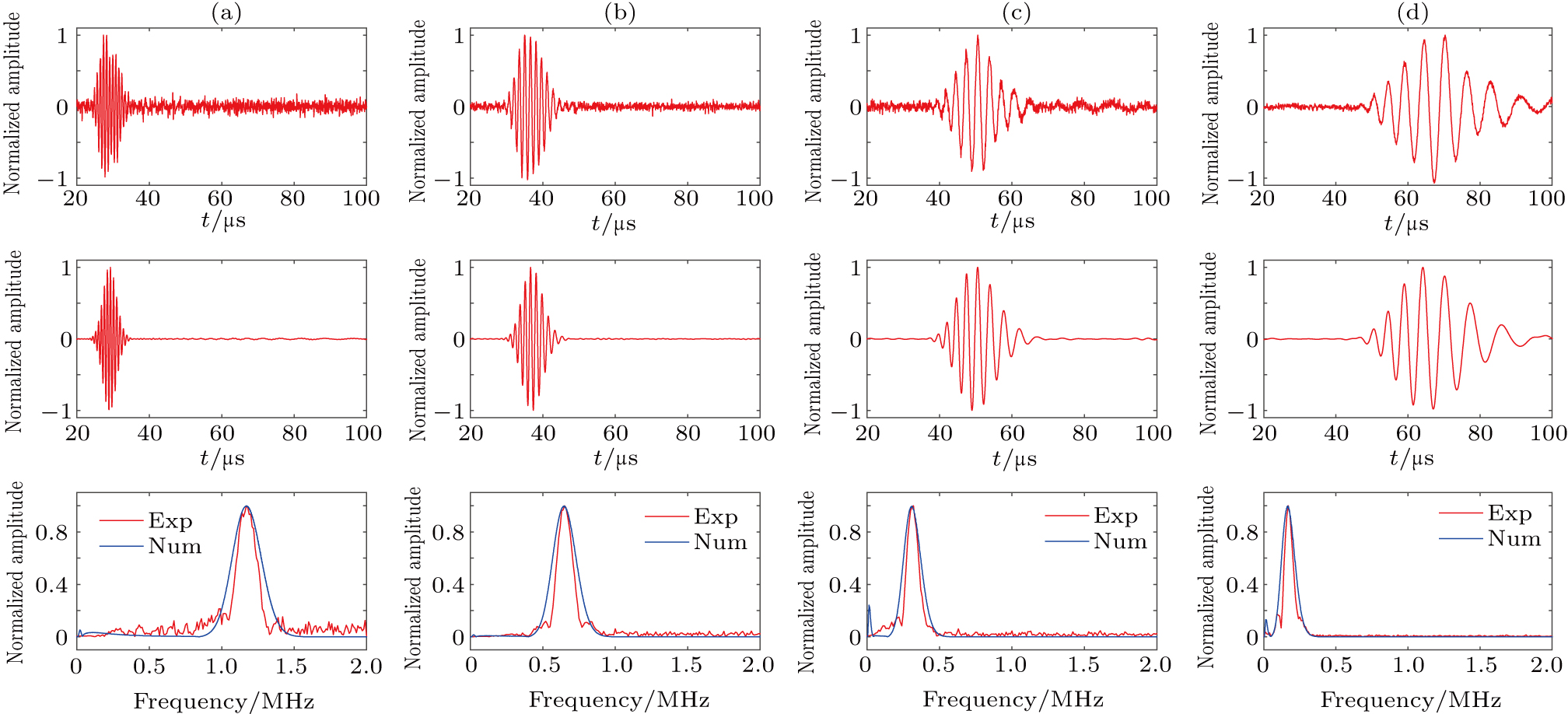
Figure
The narrowband Lamb wave was successfully generated by the laser array produced by the Michelson interference technique. Both velocity and the center frequency of the generated Lamb wave change with array spacing. Larger element spacing corresponds to lower center frequency, and vice versa. The theoretical and experimental results agree well with each other. The displacement signals in Fig.
The phase velocity and the group velocity dispersion curves of A0 mode were calculated numerically from the secular equation by using the material parameters in Table
The intersecting points between the oblique blue lines and the phase velocity curves in Fig.
Using the adjustable laser line array proposed in this paper, the selective excitation of guided wave mode will be flexible and convenient comparing with traditional laser line array generation techniques, such as lenticular arrays[11,12] and slit masks.[13–15] In this paper, only a case of the excitation of an antisymmetric A0 mode at low frequency-thickness product is given, but this method can be used for selectively exciting any other guided wave mode and higher frequency–thickness product case if an appropriate exciting laser source can be used.
In this paper, we present a method of using the Michelson interference technique to implement a new changeable spacing laser exciting array. Using this technique, the selective generation of narrowband zeroth order antisymmetric Lamb wave with a wavelength range from several hundred 
Owing to the limitation of pulsed laser source, the Lamb wave mode generation for higher frequency–thickness product case has not be conducted. One major reason is that the number of interference fringes will increase with frequency increasing for a fixed size laser beam, and thus the pulse energy of each single fringe of this array will be too weak to generate the guided wave effectively, or the signal-to-noise ratio for the generated signals becomes very bad. The other reason is that the attenuation of higher frequency ultrasonic component will increase. If a higher energy pulsed laser can be used, the excitation of Lamb wave modes for higher frequency–thickness product range may be implemented.
This method proposed in this paper may provide an engineering foundation and possibility of noncontact NDT technique for plate or pipe structures.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] |