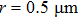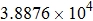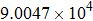1. IntroductionTo improve the precision of climate modeling and atmospheric remote sensing, radiative transfer models (RTMs) that can accurately calculate the radiation transferred through the atmosphere with aerosols and clouds are required.[1–3] As fundamental input parameters for the radiative transfer simulation, the light-scattering properties of aerosols (especially those in the solar spectrum) should be accurately modeled.[4–7] However, owing to the irregular shapes and inhomogeneous compositions of aerosol particles (such as mineral dust and soot), their light-scattering processes are not adequately understood, and substantial uncertainties still remain in their optical properties.[8,9] To simplify the scattering process of aerosol particles in the RTMs widely used at present, nonspherical aerosol particles are usually taken as spherical ones with equivalent volumes or surface areas, which will definitely decrease the computational accuracy of radiative transfer.[6,10–12] Many researchers have also found that nonspherical aerosol particles exert a significant influence on the polarized components of radiation.[6,9,13]
With the awareness of the importance of the scattering properties of nonspherical particles, many scattering calculation models have been established.[8,14,15] According to the size parameter ranges applicable to these models, they can be classified into three theoretical branches: the models in the Rayleigh regime, semi-classical scattering models, and models in the geometric-optics (or physical optics) regime. Models in the Rayleigh regime and geometric-optics regime include the Rayleigh approximation, the Rayleigh–Gans–Stevenson approximation (RGA), the anomalous diffraction theory, the bridging method,[16,17] and the geometric optics approximation (GOA).[8,18] Limited to their physical essence, they are mainly applicable to particles with sizes much smaller or larger than the light wavelength.[8] However, because the size of aerosol particles is comparable to the light wavelength in the solar spectrum, these models cannot be applied to calculate their light-scattering properties. For semi-classical scattering models, a particleʼs scattering properties are obtained by solving Maxwellʼs curl equations and Helmholtz equations analytically or numerically. Models of this type can be grouped into three categories, i.e., field expansion models, volume integral methods, and microelement models. The T-matrix method (TMM),[19,20] separation of variables method (SVM),[21] and point matching method (PMM)[22] belong to the first category, where TMM has become a widely tested model for the improvements made by Mishchenko, Bi, and other researchers.[8,19,23–25] By using these models, high calculation precision can be easily achieved with low memory consumption and high computational efficiency.[8] However, owing to the limitation of the boundary conditions for numerical calculation, most of these models can only be applied to particles with regular shapes. Moreover, their numerical simulation processes become nonconvergent for particles with large sizes, large refractive indices, or extreme shapes. The volume integral methods include the method of moments (MoMs)[26] and discrete dipole approximation (DDA).[27–29] The main advantage of DDA and the MoMs is that they can be applied to particles with any irregular shapes and inhomogeneous compositions. However, it should also be noted that although simulation accuracy will be improved with increasing dipoles, the matrix equations that need to be solved will become larger as well. Therefore, to ensure stability and efficiency of the computational process, DDA and the MoMs are mainly applicable to small particles.[30] With the development of computational electromagnetics, such micro-element models as the finite difference time domain (FDTD) and finite element method (FEM) have gradually been introduced into the light-scattering simulation of nonspherical aerosols.[31,32] The main advantage of these methods is that they can overcome the singularity of volume integral methods; thus, they are more suitable for particles with complex shapes and large sizes. However, owing to the constraints of numerical dispersion and the Courant stability condition, the spatial resolution of the computational domain should be smaller than λ/10 (where λ is the light wavelength); therefore, the time and memory consumed would be huge for the light-scattering simulation of large particles.[4]
To overcome this problem, the pseudo-spectral time domain (PSTD) was introduced into the numerical simulation of the light-scattering process by Liu and Yang.[33] In this model, the Fourier-transform-based pseudo-spectral method and the finite difference technique are used to calculate the spatial and temporal derivatives of Maxwellʼs equations, respectively.[34] Because of the excellent performance of the Fourier transform, this method can achieve very high simulation accuracy with a relatively coarse spatial resolution, and therefore it can decrease the computational time and memory dramatically.[33] Despite the excellent performance of PSTD, there are two aspects that need to be improved: first, owing to the specificity of its discretization form, the incident field is mainly introduced by a pure scattering field technique in the PSTD scheme now, which is difficult and time-consuming for particles with large size and complex shapes; second, the absorption boundary conditions (ABCs) employed in the PSTD scheme are mainly limited to Berengerʼs perfectly matched layer (BPML) and uniaxial perfectly matched layer (UPML), whose performance is relatively low compared to convolution perfectly matched layer (CPML) and ADE-PML for the FDTD scheme.[35] To improve modelʼs performance, Sun et al.[4] generalized the CPML for the PSTD model. Here, we generalize the weighted total field/scattering field (TF/SF) technique[36] and ADE-PML for the 3D-PSTD scheme and an improved PSTD scattering model of our own is established. In our scattering model, not only can the simulation errors caused by the wave reflection of ABC be reduced, but the incident wave can also be introduced without considering the actual shapes and sizes of the scatters.
The structure of our paper is as follows: in Section 2, the basic structure and principle of our PSTD model are introduced. In Section 3, the precision of the PSTD model is validated against the well-tested scattering theories for particles with different shapes and inhomogeneous compositions, and the influence of the spatial resolution and thickness of ADE-PML on the calculation accuracy of PSTD model is analyzed. In Section 4, the computational efficiency of our model is discussed. Finally, a brief summary is given in Section 5.
2. Design of the parallelized PSTD scattering model2.1. Structure of the PSTD scattering modelThe basic structure of the PSTD scattering model is presented in Fig. 1. As shown in this figure, the PSTD model is comprised of three modules, i.e., the preprocessing module, the electromagnetic field computational module, and the scattering parameter calculation module.
The preprocessing module is employed to prepare the input parameters for the light-scattering computation. These input parameters include the propagation direction and polarization states of incident light, the refractive index of the aerosol particle, and the particleʼs shapes discretized by a grid mesh. The electromagnetic field computational module is designed to calculate the electromagnetic field in the near- and far-field regions. There are three key techniques in this module, i.e., the ADE-PML technique for the truncation of the computational space, the weighted TF/SF technique for the introduction of the incident wave and the near-to-far transformation technique, where the near-to-far transformation is performed in the frequency domain, while the others are implemented in the time domain. The scattering parameter calculation module is applied to calculate a particleʼs scattering parameters based on the near and far electromagnetic field components; these scattering parameters include the absorption and extinction cross-sections, the scattering phase matrix and single scattering albedo.
2.2. Basic principle of the PSTD modelIn the PSTD model, the scattering process is simulated by numerically solving Maxwellʼs equations, where Maxwellʼs equations in an isotropic medium have the following form:
in which
and
refer to the electric and magnetic field;
ε and
μ are the permittivity and permeability of the medium;
σ and
σm represent the electric and magnetic conductivities, respectively. If the aerosol particle has a refractive index of
, then the permittivity and electric conductivity can be obtained from the refractive index
m by
,
(
ω is the angular frequency). Because most aerosol particles are in a nonferromagnetic dielectric medium, their permeability and magnetic conductivity are set as
μ = 1 and
σm = 0 in our model.
In contrast to the FDTD scheme, in the PSTD model, the pseudo-spectral method is applied to calculate the spatial derivatives of Maxwellʼs equations, whereas the time derivative is discretized by a central differential scheme. The basic principle of the pseudo-spectral method is to use Fourier integrals to obtain the derivatives of the field components, where the Fourier integrals are carried out by using the fast-Fourier-transform (FFT) algorithm. Because of the high-precision reconstruction ability of the FFT/IFFT technique, the spatial derivatives can be calculated accurately with a relatively coarse grid mesh. According to the idea of the PSTD scheme, the derivatives of the electromagnetic components along the x-, y-, and z-axes can be presented as
where
is the imaginary unit, (
) are the discrete coordinates of the field components; the algorithm operators
,
, and
refer to the first derivatives with respect to
x,
y, and
z. Nx,
Ny, and
Nz denote the grid numbers along the
x-,
y-, and
z-axes, and
,
, and
are the grid size sin the different directions. Because the particularity of the discretization form of the pseudo-spectral method, the Yee cell for the FDTD scheme is no longer applicable to the PSTD; therefore, in our model, all the electric and magnetic components are assigned to the center of grid cells, rather set them at the edges and face centers of the cells.
Because of the abrupt changes in the optical properties at the surface of aerosol particles, the electric and magnetic field will be discontinuous at the interface between the scatterer and the ambient medium, which will result in unnecessary high-frequency components in the FFT process (i.e., the “Gibbs phenomenon”). In order to suppress the generation and accumulation of the unnecessary signals, the high-frequency components in the frequency spectrum are directly truncated before the IFFT process, which is similar to the method adopted by Liu et al.[33] Taking the derivatives along the x-axis for example, after the improvement, the calculation equation for
can be rewritten as
where
is the modified algorithm operator and
Nt is the number of the truncated terms. To obtain the best performance,
Nt is usually set to be an integer ranging from
to
(
means the integer conversion).
Based on the theoretical analysis above, Maxwellʼs equations can be easily discretized by replacing the spatial derivatives with
and using the finite difference technique for the temporal derivatives. Then, the time-updating equations can be derived as
In the iterative equations above,
n is the time step, CA and CB are the iterative coefficients for the electric components, and they can be calculated by
where
is the discrete time interval. Similarly, the iterative coefficients for the magnetic components, CP and CQ, can be expressed as
Stability condition of the PSTD scheme Similar to the Courant stability condition of the FDTD scheme, the discrete time interval and spatial resolution for the PSTD scheme should satisfy certain constraints in order to guarantee the stability of its iteration process. According to the derivation of Liu,[34] the stability criterion for the PSTD scheme can be written as
where
D is the dimensionality of the computational space; in our model,
D is set to 3. From the equation above, it can be found that the requirement of the discrete time interval of the PSTD scheme is higher than that of the FDTD scheme, but because the grid size needed for the PSTD scheme is much coarser than the FDTD scheme, the corresponding time step will be larger than that of the FDTD scheme.
2.3. Design of the ADE-PML absorption boundary conditionAlthough the electromagnetic scattering process is an open-space problem, the calculation of the PSTD should be always implemented in a finite computational domain owing to the limitations of the computer memory and CPU. Therefore, approximate ABCs have to be imposed to truncate the computational domain in order to suppress wave reflections back into the domain and permit all outward-propagating wave analogs to exit the domain, almost as if the domain were infinite.
In our model, the ADE-PML, an excellent ABC used in the FDTD scheme is generalized and applied to the 3D-PSTD scheme. The main advantage of the ADE-PML is that its implementation is completely independent of the ambient medium and high absorption performance can be achieved without increasing the memory consumption. Similar to CPML, the ADE-PML can be derived from modified Maxwellʼs equations in the frequency domain[37]
where
(
i =
x,
y, or
z) is called the stretched-coordinate metric. If the expression of
si is defined as
, then the reciprocal of
si can be written as
, where
,
,
,
, and
[37] the setting of these parameters is similar to that of the FDTD scheme, and the reader can refer to the literature
[4,35] for details. Considering the similarity of derivations for the different field components, here we only take
Ex as an example to present the implementation of the ADE-PML.
Substituting
into Eq. (16) and using two auxiliary variables
and
for simplification, then Maxwellʼs equations for the component Ex can be rewritten as
Furthermore, transforming Eqs. (18) and (19) into the time domain, a group of equations describing the light propagation in ADE-PML layers can be derived as
Similar to the method adopted in Section 2.2, discretizing the differential equations above by using the pseudo-spectral method for spatial derivatives and the finite differential technique for the time domain, then the iterative equations for
,
and
can be derived as
where
and
are the iterative coefficients for
, which have the same form as Eq. (
13),
ai and
are the iterative coefficients for
and
, which can be calculated by
The implementations of the ADE-PML for the other electromagnetic field components can be similarly obtained, and thus their derivations are not presented here.
2.4. Weighted TF/SF techniqueThe introduction of an incident wave is another key technique in the PSTD scattering model. Because the spatial distribution of the electromagnetic field components is not defined by Yee cells, the traditional TF/SF technique for the FDTD scheme is no longer applicable to PSTD. Therefore, in our model, the weighted TF/SF technique proposed by Gao[36] is generalized and applied to the 3D-PSTD scheme.
Similar to the traditional TF/SF technique, the weighted TF/SF technique introduces an incident wave by adding incident terms into the connection region between the total field and the scattered field. As shown in Fig. 2, the computational domain for the PSTD model is divided into four parts: the total field region, the connection region, the scattering field region and the ADE-PML region. Within the connection region, the incident field
and
are weighted by the window function ζ, and the modified total field
and
are regarded as the sum of the scattering field and weighted incident field,
The purpose of this design is to guarantee that the electromagnetic field components can vary smoothly from the scattering field region to the total field region so that the incident wave can be introduced without causing large Gibbs errors.
In Eq. (26), the window function ζ should satisfy the following constraints: in the connection layers, ζ should change smoothly from 0 to 1.0; while in the total field region and scattering field region, ζ should be set as 1.0 and 0, respectively (as shown in Fig. 2).
The wave propagation equations in the connection region can be derived by substituting
and
into Maxwellʼs equations, written as (see Ref. [36])
The incident wave can be properly introduced by solving the equations above. However, from these equations, two problems remain to be dealt with in order to solve the equations above numerically, i.e., the selection of the window function ζ and the discretization of the modified Maxwellʼs equations.
In the weighted TF/SF technique, the selection of the window function is very important, because weighing the incident field with window functions in time domain means the convolution operation between the incident wave and window function in frequency domain. In our PSTD model, the IBH function (the integral form of the Blackman–Harris function) is set as the window function (the IBH function is widely applied to the digital signal processing field and shows the best performance[36]).
To meet the requirements of sampling accuracy, the number of sampling points in the connection layer should equal or larger than 2(M+1). For example, if M is set as 3, then an eight-layer connection region should be set at least. Because the computational space of the PSTD scattering model is three-dimensional, then the window functions should be expanded to 3D space correspondingly. In our model, the 3D window function is constructed by the product of the window functions in different directions, expressed as
 | |
After the window function is determined, another problem is the discretization of the modified Maxwellʼs equations. Similar to the method introduced in Section 2, the time-updating equations for different electromagnetic components can be easily derived by discretizing Eq. (27) by the pseudo-spectral method for space derivatives and using the central differential scheme for the time derivatives. For the sake of simplicity and generality, we only take Ex and Hx as an example to present their time-updating equations
where
, is the discrete position coordinate. From the above it can be found that the incident field can be easily introduced into the computational space by modifying the field components in the connection region with the incident field.
2.5. Near-to-far transformation and the calculation of scattering properties2.5.1. Near-to-far transformation and the calculation of the phase matrixSimilar to the FDTD scheme, the calculation of the scattering amplitude matrix and phase matrix should be based on the far electric fields obtained for two incident waves with orthogonal polarization states. Therefore, the surface integral method based on the Huygens principle is employed to transform the near-field components to their far-field in our model.
In the surface integral method, the far-field scattered by the aerosol particles is regarded as the field radiated by the equivalent electric and magnetic currents at a closed surface in the scattering field region with the scatterer inside. According to the electromagnetic equivalence theorem, the equivalent electric and magnetic currents can be calculated from the electric and magnetic components at the extrapolation surface
where
and
denote the equivalent electric and magnetic currents,
and
are the electromagnetic components at the extrapolation surface and
is the normal unit vector of the surface.
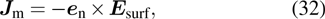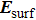
With the equivalent electric and magnetic currents obtained, the far electric field can be calculated by the following equations:
where
and
are the Hertz vectors of the equivalent currents
in which
is the Green function for 3D space. In the frequency domain, we can replace
with
, and then the scattered electric field can be modified as
where
is the normalized wave vector along the scattering directions. By using Eq. (
36), the electric field in the far-field region can be calculated from the field components at the extrapolation surface. If the far electric field is obtained for the incident waves with transverse electric (TE) and the transverse magnetic (TM) modes, respectively, then the scattering phase matrix
can be calculated by
where (
θ,
φ) are the scattering directions,
and
are the amplitude of the incident wave perpendicular and parallel to the scattering plane,
and
are the vertically polarized and horizontally polarized components of the scattering field for
, while
and
are scattered electric fields for
. According to the definition of scattering phase matrix, the phase matrix can be calculated from
[8,15] directly.
2.5.2. Calculation of integral scattering parametersThe integral scattering properties of aerosol particles include absorption cross-sections, extinction cross-sections, scattering cross-sections and single scattering albedo. These parameters reflect the total ability of the aerosol to absorb and scatter electromagnetic waves. The calculation models for these parameters are similar to those designed for the FDTD and the MRTD,[14] where the absorption cross-section Cab can be computed by normalizing the energy depleted by aerosols with the total energy of the incident wave[14]
where
Z0 is the wave impedance of vacuum, and
is the intensity vector of the incident electric field.
is the position vector of the electric components, and the operator
denotes the conjugation of a complex number.
The extinction cross-section Cext can be calculated by the volume integral of the extinction Poynting vector
[14]
in which
denotes the imaginary part of a complex number and
ω is the angular frequency of an incident wave. Once
Cext and
Cab are obtained, the scattering cross-section
Csc can be calculated by
.
3. Model validation and result analysisThe PSTD scattering model for nonspherical aerosol particles was coded by Fortran 90, and the OpenMP technique was employed for the parallelization of the model. To quantitatively evaluate the performance of the PSTD scattering model, the results of this model are compared with those obtained from the well-tested models such as the Lorenz–Mie theory, Aden–Kerker theory and TMM in this section for spherical particles, inhomogeneous particles and nonspherical particles.
3.1. Model validation for spherical particlesThe scattering phase matrices simulated by the PSTD scattering model is first validated against Lorenz–Mie theory for two spherical particles, a small one and a large one.
Figure 3 shows the phase matrices simulated by PSTD and Lorenz–Mie scattering theory for a small particle with a radius of
. In this figure, the simulation accuracy of the phase function (i.e., F11) is evaluated by the relative errors, whereas for the ratios,
,
, and
, their computational precision is presented by absolute errors. In this simulation, the wavelength of incident light is set as
, the refractive index of the particle is set as
and the computational space is discretized by a grid mesh with a spatial resolution of λ/24.
As can be seen from the figures, the nonzero phase matrix elements obtained by PSTD closely agree with the exact solutions given by the Lorenz–Mie theory well, where in forward directions (
), the maximum simulation error of F11 is just 2.43%, and the absolute errors of
,
, and
are only 0.023, 0.0284, and 0.022, respectively, indicating the high precision of the PSTD model. The simulation accuracy at large scattering angles is relatively low compared to that in the forward directions and the simulation errors of F11,
,
, and
are up to 11.2%, 0.065, 0.0577, and 0.0581. This phenomenon can be explained by stair approximation errors, because the particle is approximated by cubic cells in the PSTD model, the constructed shape for calculation is slightly different from the actual sphere we have assumed; furthermore, because the scattering phase matrices are more sensitive to a particleʼs shape in backscattering directions than in forward directions, larger simulation errors will occur at large scattering angles correspondingly.
The precision of the PSTD model is further validated for a large spherical particle with a size parameter of nearly 100. In this test, the light wavelength and the refractive index are the same as those for the small one; the radius of the particle is set as
and is discretized by a grid mesh of λ/12. Similarly, the scattering phase matrices are calculated by different models, and the simulation errors of the phase matrix elements are also calculated and presented in Fig. 4.
From the figure, it can be found that the results of the PSTD scheme show excellent consistency with those of the Lorenz–Mie theory in terms of their overall variation patterns, illustrating that our PSTD model can simulate the scattering properties of large particles with reasonable precision. For the scattering phase function, its simulation errors fluctuate with scattering angle notably with their values ranging from near-zero in forward directions to 38.5% at the scattering angle near 180°. For
,
, and
, the absolute simulation errors are less than 0.2 for scattering angles smaller than 100°, however for the backward scattering directions, their simulation errors are much larger though the variation patterns of the curves of different models are similar. Compared with the results of the small particles, it can also be found that the simulation accuracy for large particles is notably lower than that for the small ones, which is similar to the conclusion drawn by other researchers.[38]
To validate the PSTD modelʼs ability to calculate the integral scattering properties of aerosol particles, the extinction efficiency Qext, absorption efficiency Qab and single scattering albedo ω are calculated for particles with different sizes, and the results are listed in Table 1. In this test, the light wavelength is set as
, the refractive indices of these particles are all set as
, and their size parameters are taken to be 6.28, 10, 20, 40, 60 and 80, respectively. As can be seen, a good agreement is achieved between the results of the PSTD model and Lorenz–Mie theory, indicating that the PSTD model can calculate particles’ integral scattering parameters with high precision, where the simulation errors of Qext and ω are generally smaller than 1%. On the whole, the calculation accuracy of Qext is higher than that of Qab, and the single scattering albedo achieved the smallest simulation errors among the three parameters. With the increase of particle size, the simulation accuracy of our model is reduced as well.
Table 1.
Table 1.
 Table 1.
Comparison of the integral scattering parameters simulated by Lorenz–Mie theory and the parallelized PSTD scattering model.
.
| x
|
Grid size |
Extinction efficiency Qext
|
Absorption efficiency Qab
|
Single scattering albedo |
| Lorenz–Mie |
PSTD |
Re/% |
Lorenz–Mie |
PSTD |
Re/% |
Lorenz–Mie |
PSTD |
Re/% |
| 6.28 |
λ/24 |
3.7725 |
3.7732 |
0.0203 |
0.0207 |
0.0202 |
−2.1432 |
0.9945 |
0.9946 |
0.0132 |
| 10 |
λ/24 |
2.6677 |
2.6793 |
0.4354 |
0.0349 |
0.0342 |
−1.7328 |
0.9869 |
0.9871 |
0.0304 |
| 20 |
λ/24 |
2.4800 |
2.4854 |
0.2213 |
0.0714 |
0.0692 |
−2.9901 |
0.9712 |
0.9721 |
0.0960 |
| 40 |
λ/24 |
2.3392 |
2.3492 |
0.4295 |
0.1131 |
0.1102 |
−2.5366 |
0.9516 |
0.9531 |
0.1553 |
| 60 |
λ/16 |
2.2617 |
2.2850 |
1.0321 |
0.1659 |
0.1596 |
−3.7400 |
0.9266 |
0.9301 |
0.3791 |
| 80 |
λxs/12 |
2.1810 |
2.2240 |
1.9732 |
0.2110 |
0.2022 |
−4.1443 |
0.9033 |
0.9090 |
0.6376 |
Note: Re denotes the relative errors in percentage, which are defined as:
, where
is the results obtained by PSTD, and
is the results obtained by the Lorenz–Mie theory.
| Table 1.
Comparison of the integral scattering parameters simulated by Lorenz–Mie theory and the parallelized PSTD scattering model.
. |
3.2. Model validation for particles with inhomogeneous compositionsFor the case of inhomogeneous particles, the PSTD model is validated against the Aden–Kerker theory for a sphere with a core–mantle structure. In this test, the wavelength of incident light is set as λ =
, the particle is taken as a concentric sphere with an inner radius of
and an outer radius of
, and the refractive indices of core sphere and the coated spherical shell are set as
and
, respectively. The computational domain containing the particle is discretized by cubic cells with an edge length of λ/24. Then, the phase matrices are calculated by the PSTD model and Aden–Kerker theory, and the results are shown in Fig. 5.
The curves of the phase matrix elements obtained by the PSTD model approximately coincide with those of the Aden–Kerker theory, where the relative simulation errors of F11 are less than 10% for most scattering angles, and the absolute errors of
,
, and
are generally less than 0.1. Overall, the simulation errors in the forward scattering directions are much larger than those at large scattering angles, which is similar to the conclusion we have drawn in Section 3.1. In terms of the variation of the error curves, it can also be found that the angular distribution of simulation errors correspond to the variation patterns of the phase matrix elements, namely, large simulation errors usually appear in peaks and troughs of the curves of matrix elements.
3.3. Model validation for homogenous nonspherical particlesThe precision of the PSTD model is also investigated for nonspherical particles by comparing the scattering phase matrix and integral scattering parameters calculated by the PSTD model with the exact solutions of the T-matrix method.
To illustrate the performance of the PSTD in phase matrix calculation, the nonzero phase matrix elements of a cylindrical particle are given in Fig. 6. In this test, the light wavelength is taken as
, and its propagation direction is perpendicular to the undersurface of the cylinder; the diameter (D) and length (L) of the particle are all set as
, and its refractive index is taken as
the spatial resolution for discretization is the same as that of the small sphere.
From the figure, it can be easily found that excellent agreement is achieved between the results of the PSTD model and the TMM, validating the precision and reliability of our model. For the scattering phase function, its simulation errors are generally smaller than 10% at scattering angles ranging from 0° to 90°; in the backward scattering directions, the simulation accuracy is reduced to some extent, but its simulation errors are smaller than 15% for most scattering angles. The angular distribution of the simulation errors of
,
, and
are similar to that of F11, namely, their modeling accuracy in the forward directions is notably higher than that at large scattering angles, where for
, the maximum error in 0°–80° is smaller than 0.05, while at scattering angle 121°, the simulation error is up to 0.302. At the scattering angles where the phase matrix elements fluctuate rapidly, the simulation errors are also notably larger than those at other directions, which is similar to the spherical and concentric particles.
To further test the modeling accuracy of the PSTD model for integral scattering properties, the extinction efficiencies (Qext), absorption efficiencies (Qab) and scattering efficiencies (Qsc) of the cylinders are also calculated by the PSTD model and the TMM, respectively, and the results are listed in Table 2.
Table 2.
Table 2.
Table 2.
Comparison of the integral scattering parameters calculated by the PSTD model and the T-matrix method.
.
| m
|
(D, L) |
|
|
|
| PSTD |
TMM |
Re/% |
PSTD |
TMM |
Re/% |
PSTD |
TMM |
Re/% |
|
(1,1) |
3.7243 |
3.7157 |
0.2314 |
0.0157 |
0.0158 |
−0.6329 |
3.7086 |
3.6999 |
0.2351 |
| (1,2) |
3.7527 |
3.7414 |
0.3020 |
0.0196 |
0.0201 |
−2.4876 |
3.7331 |
3.7213 |
0.3171 |
| (2,1) |
2.6408 |
2.6275 |
0.5062 |
0.0250 |
0.0254 |
−1.5748 |
2.6158 |
2.602 |
0.5304 |
|
(1,1) |
2.0848 |
2.0776 |
0.3466 |
0.0322 |
0.0325 |
−0.9231 |
2.0526 |
2.0451 |
0.3667 |
| (1,2) |
2.1327 |
2.1146 |
0.8559 |
0.0399 |
0.0407 |
−1.9656 |
2.0928 |
2.0738 |
0.9162 |
| (2,1) |
2.3523 |
2.3317 |
0.8835 |
0.051 |
0.0519 |
−1.7341 |
2.3013 |
2.2798 |
0.9431 |
Note: Re denotes the relative errors in percentage, which are defined as:
, where
are the results obtained by the PSTD model, and
are the results obtained by the T-matrix method.
| Table 2.
Comparison of the integral scattering parameters calculated by the PSTD model and the T-matrix method.
. |
It can be found that the relative errors of the extinction and scattering are all smaller than 1% for particles with different shapes and refractive indices, and the errors of the calculated absorption efficiencies are generally smaller than 2%, indicating the high calculation accuracy of the PSTD model for nonspherical particles. On the whole, the extinction efficiencies obtained by the PSTD model are larger than those of the TMM, while the absorption efficiencies are generally underestimated for most cases. From the variation of the simulation errors, it can be found that the simulation accuracy of the integral scattering properties is gradually reduced with the increase of refractive index.
3.4. Model validation for inhomogeneous nonspherical particlesThe model is further validated with the DDASCAT developed by Draine and Flatau.[28] In this process, the particle is set as a spheroid with a spherical core, where the horizontal axis and the rotational axis of the spheroid are set as
and
, and the radius of the spherical core is taken as
, and their refractive indices are set as
and
, respectively. The spatial resolution for PSTD calculation is the same as cylinder particles, and the number of dipoles for DDA calculation is set as 226088. The phase matrices simulated by different models are shown in Fig. 7.
As can be seen from these figures, the phase matrices obtained by DDASCAT and the PSTD model show good consistency, where the scattering phase functions obtained by the two models almost coincide with each other and their relative discrepancies are less than 10% for all directions; for
,
, and
, their absolute discrepancy is smaller than 0.1 for most scattering angles. From the results, we find that our PSTD model is also effective for inhomogeneous nonspherical particles.
The integral scattering properties obtained by the PSTD model are also compared with those obtained by DDASCAT for three inhomogeneous nonspherical particles, the results are presented in Table 3. In this simulation, the shape and compositions of the particles are similar to those in the scattering phase matrix simulation. From the table, we find that both Qext and Qab calculated by the PSTD model show good agreement with those of DDASCAT, and the relative simulation errors of Qext are less than 2%; the calculation accuracy of Qab is slightly lower than Qext, and its errors are smaller than 5%.
Table 3.
Table 3.
Table 3.
Comparison of the integral scattering parameters calculated by the PSTD model and DDASCAT.
.
| (a,b) |
Dipoles (DDA) |
Grid size (PSTD) |
|
|
| PSTD |
DDA |
Re/% |
PSTD |
DDA |
Re/% |
| (1,2) |
226088 |
λ/24 |
1.4401 |
1.4619 |
−1.4912 |
0.0401 |
0.0420 |
−4.5238 |
| (1.5,1) |
158320 |
λ/24 |
2.3884 |
2.4278 |
−1.6228 |
0.0397 |
0.0410 |
−3.1707 |
| (2,1) |
262000 |
λ/24 |
4.5393 |
4.6297 |
−1.9526 |
0.0408 |
0.0429 |
−4.8951 |
Note: all particles are set as a spheroid with a spherical core (
). The light wavelength and particle refractive indices are the same as those in the scattering phase matrix simulation. The relative errors are calculated in the same way as in Tables 1 and 2.
| Table 3.
Comparison of the integral scattering parameters calculated by the PSTD model and DDASCAT.
. |
3.5. Influence of parameter settings on the modelʼs performance3.5.1. Analysis of effect of the spatial resolution on the modelʼs simulation accuracySpatial resolution is not only an important factor determining the construction accuracy of a particleʼs shape, but it is also a parameter influencing the discretization accuracy of Maxwellʼs equations. Owing to this reason, the influence of the grid size on calculation accuracy is systematically investigated in this section. To quantitatively evaluate the modeling precision, we use the following parameters to evaluate the performance of the PSTD model, i.e., the relative simulation errors of integral scattering parameters, the square root error of the scattering phase function and linear
(namely, RSEF11 and RSEF12)
Table 4 lists the modeling accuracy of the PSTD model for different spatial resolutions, in this case, the light wavelength is set as
, and the particles are all taken as spherical with a refractive index of
.
Table 4.
Table 4.
| Table 4.
Influence of grid size on the simulation accuracy of aerosol scattering properties.
. |
As shown in the table, with the increasing spatial resolution, the modeling accuracy of the phase function and integral scattering parameters are improved as well on the whole, where for particles with a size parameter of 10, in case that the grid size increases from λ/8 to λ/20, RSEF11 decreases from 11.6672% to 6.7534%, and RSEF12 is reduced by 0.1025. It can also be found that even if the spatial resolution is as low as λ/8, very high calculation accuracy can still be achieved by the PSTD model, especially for large particles. This phenomenon can be explained by the high-precision reconstruction ability of the pseudo-spectral method, because the FFT/IFFT technique is used in the PSTD model, very high precision can be achieved even with a spatial resolution near the Nyquist sampling limit, thus the spatial derivatives can be calculated accurately with a relatively coarse grid mesh. When the spatial resolution is given, the modeling accuracy is reduced as the increase of particle size. According to simulation errors for particles of different size, if we take the required precision criteria as follows: (i) the relative error of Qext is less than 1%, (ii) RSEF11 is less than 25%; then we can find that, for particles with
, a spatial resolution of λ/24 is enough for scattering simulation, for particles with
, a spatial resolution of λ/16 is enough.
3.5.2. Analysis of effect of the thickness of the ADE-PML on the modelʼs simulation accuracyThe performance of ABC is also an important factor influencing modeling accuracy, because the electromagnetic field reflected by ABC layers can alter the exact distribution of the field components. Generally, the thicker the ADE-PML is, the better the absorption ability of ADE-PML can be achieved, but the computational burden will be increased as well. Therefore, it is necessary to analyze the ADE-PML performance and determine the optimal thickness of the ADE-PML for the PSTD scattering calculations.
For this purpose, the simulation accuracy of a scattering phase matrix for ADE-PML layers with different thickness is first investigated and their performance is compared with that of a six-layer BPML (BPML is widely applied in the traditional PSTD model). In this simulation, the light wavelength is set as
, the particle is taken as a sphere with a radius of
, and a refractive index of
, the grid size for the particle discretization is set as λ/24, and then the calculation errors of the nonzero phase matrix elements are calculated by comparing the results with Lorenz–Mie theory, as shown in Fig. 8.
As can be seen, with the increasing thickness of the ADE-PML, the calculation accuracy is improved correspondingly, where when the thickness of the ADE-PML is larger than six layers, the error curves are almost coincident with each other, indicating that the modeling accuracy is not affected by the electromagnetic reflection of the ADE-PML. Simulation errors were mainly caused by the starting approximation of particle shape and the discretization of Maxwellʼs equations. Therefore, we can conclude that an ADE-PML with a thickness larger than six layers is enough for a scattering simulation. Comparing the results of the six-layer ADE-PML and BPML, it can be found that although their variation patterns are similar, the simulation errors of ADE-PML is slightly smaller than that of BPML, indicating that the performance of ADE-PML is better than BPML in PSTD calculation.
The performance of the ADE-PML was also investigated for integral scattering properties, and the results are demonstrated in Table 5. From the table, it can be found that the performance of the six-layer BPML and ADE-PML are similar in integral scattering parameter calculation, both their simulation errors are less than 1%. As the thickness of the ADE-PML increases, the simulation precision of the extinction cross-section Cext, absorption cross-section Cab, and scattering cross-section Csc are improved as well, where in case that the ADE-PML increases from four layers to six layers, the calculation errors of Cext and Csc are reduced by 0.4376% and 0.448%. When the number of ADE-PML layers is larger than six, the improvement in the modeling accuracy is gradually reduced as the number of ADE-PML layers increase, and the simulation errors tend to be a relatively stable value, which is similar to the results of phase matrix simulation.
Table 5.
Table 5.
| Table 5.
Influence of the thickness of ADE-PML layer on the modeling accuracy of the integral scattering properties (spheroid case).
. |
The performance of the ADE-PML is further evaluated for spheroidal particles, and the results are shown in Fig. 9. In this case, the light wavelength and spatial resolution are set as λ/24, and the horizontal axis and rotational axis are set as
and
, respectively. Similar to the spherical particle case, when the ADE-PML is thicker than six layers, the simulation accuracy of the phase matrix elements is no longer improved, indicating that a six-layer ADE-PML is thick enough for light-scattering simulation. The performance of the six-layer BPML is slightly worse than that of the four-layer ADE-PML, which demonstrates the superiority of the ADE-PML model.
4. Analysis of the modelʼs computational efficiencyThe parallel computational efficiency of the PSTD model is evaluated in this section. In this test, the light wavelength is
and the particles for calculation are taken as spheres with a size parameter of 10, 20, 40, and 80, respectively. To quantitatively evaluate the modelʼs efficiency, the simulation processes are performed in serial mode and parallel mode, and their computational time is compared with that of the traditional PSTD model designed by Berenger and the pure scattering field technique; during the calculations, the CPU time, parallel acceleration ratio Sp and computational efficiency for a single processor η is are recorded and calculated, as presented in Table 6. All the simulations are performed on the same computer, whose CPU is an Intel(R) Xeon(R) CPU E5-2630 v4 (2.2 GHz).
Table 6.
Table 6.
| Table 6.
Parallel computational efficiency of the PSTD scattering model.
. |
From the table, we find that the computational time of the PSTD model is reduced dramatically after the parallelization design, where for a particle with a size parameter of 20, the parallel acceleration ratio Sp reaches 3.8148 when six processors are used. It also can be found that η decreases as the number of processors increases; this can be explained by the increase of the communication time between different processors. Compared with the traditional PSTD model, it is also found that the improved PSTD model can reduce the computational time to some extent, where for the particle with a size parameter of 40, the time needed can decrease by approximately 9%.
5. ConclusionThe uncertainties of the scattering properties of aerosol particles with irregular shapes and inhomogeneous compositions are an important factor limiting the modeling accuracy of radiative transfer. To this end, a light-scattering model based on the PSTD technique is presented. Using this model, scattering by particles with arbitrary shapes can be effectively simulated. In this model, the ADE-PML, an excellent absorption boundary condition for FDTD, is generalized and applied to the PSTD scheme; the weighted TF/SF technique is employed to introduce an incident wave into the 3D computational domain; and to obtain the electromagnetic field in the far region, the surface-interpolation method based on the Huygens principle is used for the near-to-far transformation. The precision of the PSTD model is validated by comparing its results with those of the Lorenz–Mie theory, TMM, DDASCAT and Aden–Kerker theory, and the influence of the spatial resolution and thickness of the ADE-PML on the modeling accuracy is analyzed as well. Several conclusions are drawn as follows.
(i) The calculation results of the PSTD model, irrespective of the scattering phase matrix or the integral scattering parameters, show great consistency with those of the well-tested scattering models, indicating the high simulation accuracy of our model.
(ii) With the decreasing of the spatial resolution, the calculation accuracy of the PSTD models is improved as well. For particles with size parameters smaller than 40, a grid size of λ/24 is fine enough for light-scattering simulation, whereas for particles with size parameters larger than 40, a spatial resolution of λ/16 is enough.
(iii) The performance of the ADE-PML is closely dependent on its thickness. To suppress the wave reflections back into the domain, the thickness of the ADE-PML should be larger than six layers.
