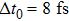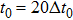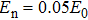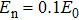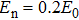Cite this Article
Yu Linpeng, Xu Yi, Wu Fenxiang, Yang Xiaojun, Zhang Zongxin, Wu Yuanfeng, Leng Yuxin, Xu Zhizhan. Nonlinear spectral cleaning effect in cross-polarized wave generation. Chinese Physics B, 2018, 27(5): 054214  
Permissions
Nonlinear spectral cleaning effect in cross-polarized wave generation
Yu Linpeng1, 2, Xu Yi1, †, Wu Fenxiang1, 2, Yang Xiaojun1, Zhang Zongxin1, Wu Yuanfeng1, Leng Yuxin1, ‡, Xu Zhizhan1
State Key Laboratory of High Field Laser Physics, Shanghai Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Shanghai 201800, China
University of Chinese Academy of Sciences, Beijing 100049, China

 

† Corresponding author. E-mail: xuyi@siom.ac.cn lengyuxin@mail.siom.ac.cn

Abstract

The underlying mechanism of the spectral cleaning effect of the cross-polarized wave (XPW) generation process was theoretically investigated. This study shows that the spectral noise of an input spectrum can be removed in the XPW generation process and that the spectral cleaning effect depends on the characteristics of the input pulses, such as the chirp and Fourier-transform-limited duration of the initial pulse, and the modulation amplitude and frequency of the spectral noise. Though these factors codetermine the output spectrum of the XPW generation process, the spectral cleaning effect is mainly affected by the initial pulse chirp. The smoothing of the spectrum in the XPW generation process leads to a significant enhancement of the coherent contrast.

PACS: 42.65.Sf;42.65.-k;42.65.Re
Keyword:nonlinear optics;cross-polarized wave generation;spectral cleaning effect
1. Introduction

High temporal contrast, which is the intensity ratio between the pulse peak and the background, is an essential property for ultrashort laser sources used in high-field physics experiments. For petawatt laser systems, the required temporal contrast is above 1010 to avoid ionization of the target before the arrival of the main intense pulse.[1,2] Efforts have been made to improve the incoherent contrast related to the amplified spontaneous emission or parametric fluorescence in different amplification stages (psscale to nsscale).[3–6] Cross-polarized wave (XPW) generation has been successfully used to improve the incoherent contrast by several orders of magnitude without introducing any spatial or spectral distortions, thereby proving to be a simple, efficient, and reliable pulse cleaning technology in high-peak-power laser systems.[7–11]

A recent breakthrough in ultrafast laser science has been the ability to produce laser pulses with a duration close to the optical cycle, i.e., few-cycle duration. Few-cycle laser pulse production has advanced the research progress of attosecond physics[12,13] and electron acceleration.[14,15] However, compared with high-peak-power laser systems, such few-cycle laser pulses should feature not only a very low level of amplified spontaneous emission (incoherent contrast), but also a high spectral quality to minimize the intensity of the coherent pedestal and satellite pulses (coherent contrast, sub-ps-scale).[16] Once again, XPW generation has demonstrated its capability to satisfy these two requirements for both temporal and spectral cleaning effects.[16–19]

Generally, degraded coherent contrast occurs not only because of the influence of the high-order spectral phase but also because of the strong modulations and sharp features of spectral amplitude.[20] Even with an ideal flat spectral phase, such spectrums lead to broad wings in the temporal domain.[21] During the XPW generation process, the sharp features and fast modulations of the input spectrum are able to be cleaned. A clean spectrum can lead to a significant enhancement of the coherent contrast.[18] However, the underlying mechanism of the spectral cleaning effect is still unknown.

In this study, the underlying mechanism of the spectral cleaning effect in the XPW generation process was theoretically investigated. An analytical formula for the output spectrum was obtained by which the evolution of the spectral noise during the XPW generation process was investigated. To obtain a comprehensive understanding of the spectral cleaning effect, the effects on the spectral cleaning induced by the chirp of the input pulses, the Fourier-transform-limited (FTL) duration of the initial pulses, and the modulation amplitude and frequency of the spectral noise were analyzed in detail. Though all of these characteristics codetermine the output spectrum of the XPW generation process, the spectral cleaning effect is more affected by the initial pulse chirp. It is demonstrated that the smoothing of the spectrum in the XPW generation process leads to a significant enhancement of the coherent contrast.

2. Theoretical analysis
2.1. Hypothesis

The input pulses are assumed to be Gaussian in the temporal and spectral domains. For an initial pulse chirp, only the quadratic spectral phase is considered, while the higher order is neglected in our investigation. The expression of the electric field corresponding to the initial unchirped pulse with a carrier frequency ω0 and amplitude E0 can be written as

The term Γ0 is related to the FTL pulse duration by . Then, the pulse chirp and spectral noise are introduced to Eq. (1). The pulse chirp is denoted as the quadratic spectral phase coefficient ψ(fs2). The modified expression can be written as[22]
where Enoise is the spectral modulation signal, i.e., spectral noise. It is assumed that the spectral noise is a cosinusoidal modulation , where En and t0 are the amplitude and frequency of the cosinusoidal modulation, respectively. This is a simple description of a spectral modulation but allows the derivation of the useful analytical formulas to reveal the main physical mechanics.[23]

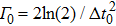
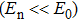
In the temporal domain, the input field E(t) is obtained by the inverse Fourier transformation of Eq. (2) as

where and . K is a constant coefficient in the Fourier transformation.

2.2. Spectral characteristics of generated pulse

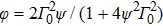
Now the characteristics of the output pulse can be determined from the input pulse characteristics. Using the convolution theorem, we have

As the generated field is proportional to and using Eq. (3), an expression for EXPW at the frequency ω0 is obtained as where and . As the higher-order term of En is negligible, only the first order is significant and reserved in the expansion in deriving Eq. (5). Therefore, the output electric field from the Fourier transformation of Eq. (5) is
where . The output electric field depends on four parameters: the chirp ψ, the FTL duration of the input pulse, and the modulation frequency t0, and modulation amplitude En of the spectral noise. These factors codetermine the performance of the output spectrum. A detailed analysis of Eq. (6) is presented in the following sections.

2.2.1. Pulse without spectral noise

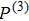
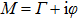
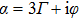
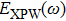
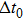
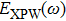
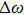
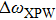
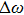
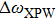
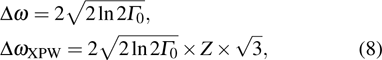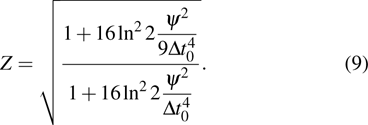First, the simplest case is considered where the spectral noise is negligible (En =0). Then the generated electric field and are given by

The effective width of the initial input spectrum is denoted as and as for the generated spectrum. Using Eqs. (1) and (7), expressions for and are obtained as
with

Equation (8) shows that for a negligible chirp, the output spectrum can be broadened by a factor of . The expansion coefficient is corrected by the Z term defined by Eq. (9) which strongly depends on the initial FTL duration and chirp of the input pulse ψ. This result is in agreement with the conclusion in Ref. [24] which demonstrates the validity of our derivation.

2.2.2. Pulse with spectral noise

The modulation terms in Eq. (6) represent the output spectral noise in the XPW generation process. To have an intuitive understanding of the evolution, the initial chirp is set to zero. Then equation (6) is simplified as

with
For a relatively high modulation frequency, such as , the negligible value of in Eq. (10) means that the spectral noise can be effectively eliminated in the XPW generation process when the initial chirp is zero, and therefore an efficient spectral cleaning effect can be observed.

For the generation of high-contrast few-cycle laser pulses, by combining the hollow-core fiber post compression with XPW generation,[16] the input pulse for XPW generation is generally modulated by a high-frequency noise. After carefully compensating for the chirp of the input pulses, the following XPW generation process always features a good spectral cleaning property that enhances the coherent contrast.[16,25] The spectral cleaning effect experimentally demonstrated in Refs. [16] and [25] is in accordance with our aforementioned theoretical analysis.

3. Analysis of spectral cleaning effect in XPW generation process

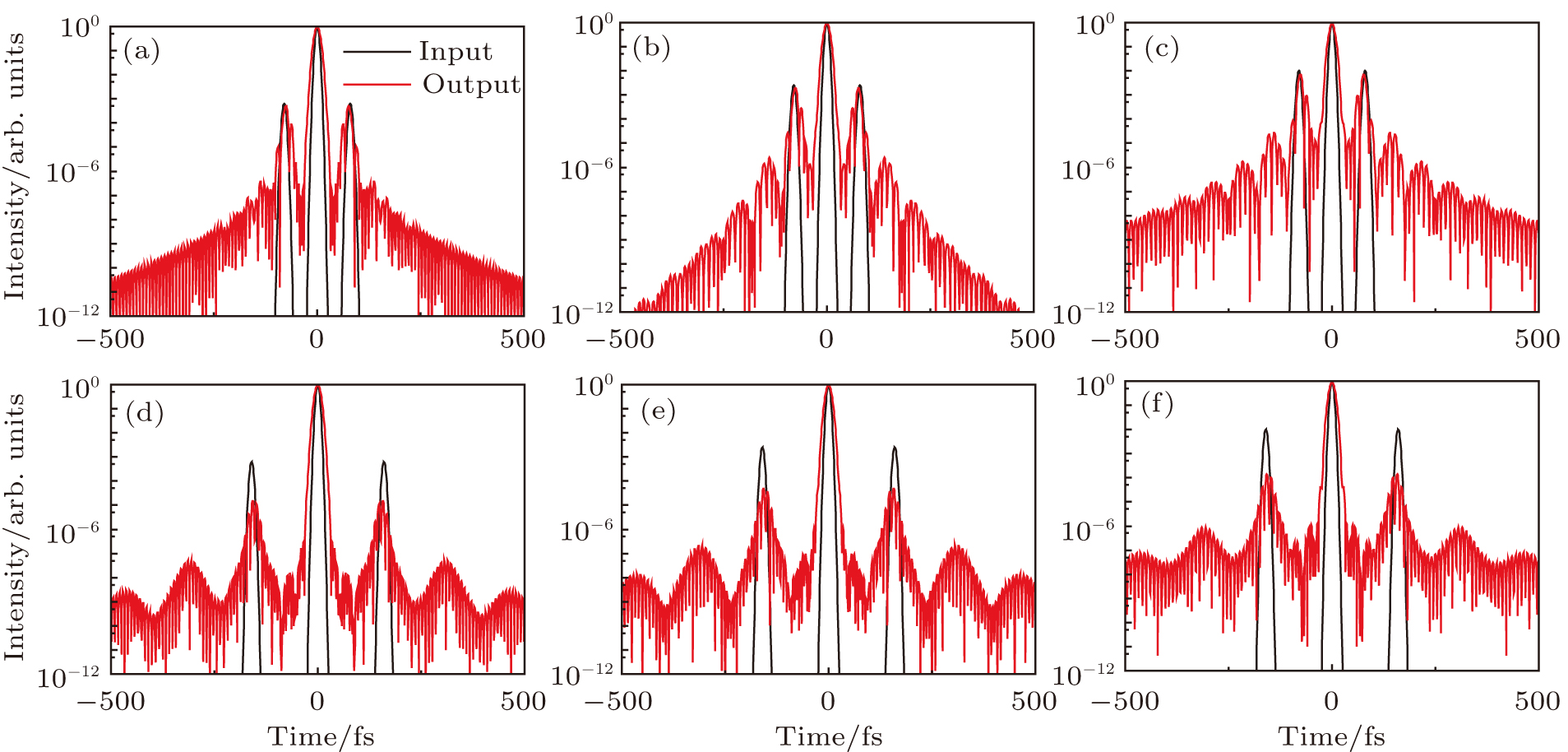
Equation (6) reveals the information of the output spectral noise. To gain a better understanding of the spectral cleaning effect, the effects on spectral cleaning induced by the input pulse characteristics were analyzed by directly solving Eq. (6).

3.1. Effect on spectral cleaning induced by initial pulse chirp

Assuming that the FTL pulse duration of the input pulse is 8 fs, the modulation amplitude and frequency of the spectral noise are and , respectively. The output spectra for different initial chirps are plotted in Fig. 1(a). For input pulses that have been perfectly compressed, the XPW generation process exhibits a good spectral cleaning effect where the output spectrum is smooth and unmodulated. Then as ψ increases, the output spectrum worsens. When the initial chirp rises to 150 fs2, the output spectrum is still smooth but much narrower than that of the unchirped case. This phenomenon has been discovered and interpreted in previous work.[24] When the initial chirp rose to 500 fs2, wrinkles appeared in the output spectrum. Only when the initial chirp was small, e.g., 30 fs2, did the spectral cleaning effect and spectral broadening exist simultaneously. The related temporal signals are plotted in Fig. 1(b). The temporal signals are the Fourier transformation of the corresponding spectrum. The best coherent contrast was obtained when the input pulse was perfectly compressed and the pre- and post-pulses induced by the spectral modulation were totally removed. For a large initial chirp, the coherent contrast deteriorated significantly. Obviously, the initial chirp is of great significance in the spectral cleaning effect as well as the temporal contrast. Therefore, in the experiments, the initial quadratic spectral phase was controlled carefully to be close to zero.

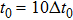
Fig. 1. (color online) (a) Output spectrum and (b) corresponding temporal contrast, for different initial chirps. The solid line with shading shows the input spectrum ( , .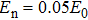

To further demonstrate the importance of the initial chirp, the spectral cleaning effect was investigated under different spectral noise conditions when the initial chirp was close to zero. The influence of amplitude and frequency on spectral noise is plotted in Fig. 2 with an initial chirp of 30 fs2. The results show that, no matter how the spectral noise varied, the output spectrum remained smooth and unmodulated. The properties of the spectral noise have a negligible influence on the performance of the output spectrum. Therefore, it is concluded that in the case of a negligible initial chirp, the influence of the other input pulse characteristics can be ignored. The performance of the spectral cleaning effect is mainly constrained by the initial chirp. Therefore, the subsequent analysis of the influence of the other input characteristics is based on the condition of a nonzero initial chirp.

Fig. 2. (color online) Calculated output spectrum for ((b), (c)) and ((a), (d)). In panels (a) and (b), , and in panels (c) and (d), for . The black and red lines denote the input and output pulses, respectively.
3.2. Effects on spectral cleaning induced by modulation amplitude and frequency of the spectral noise

Considering an input FTL pulse duration of 8 fs and an initial chirp of 300 fs2, for a relatively low modulation frequency, wrinkles still exist in the output spectrum (Figs. 3(a), 3(b), and 3(c)). However, for a relatively high modulation frequency, the output spectrum is cleaner (Figs. 3(d), 3(e), and 3(f)). It is clear that spectral noise with a higher modulation frequency can be removed more efficiently during the XPW generation process.

Fig. 3. (color online) Calculated output spectrum for different initial spectral noise. Panels (a), (b), and (c) are calculated for . Panels (d), (e), and (f) are calculated for . For panels (a) and (d), ; panels (b) and (e), ; and panels (c) and (f), . The FTL pulse duration of the input pulse is 8 fs. The initial chirp is 300 fs2.

In Figs. 3(a), 3(b), and 3(c), the spectral noise, having a lower modulation amplitude, generates a smoother output spectrum. The spectral cleaning effect is poor for a high modulation amplitude. Nevertheless, as shown in Figs. 3(d), 3(e), and 3(f), no matter how the modulation amplitude changes, the output spectrum remained smooth and unmodulated. The spectral cleaning effect seems independent of the modulation amplitude in the case of a high modulation frequency. This is attributed to the modulation frequency having a much greater influence on the spectral cleaning effect than that of the modulation amplitude.

The temporal contrast calculated from the spectrum in Fig. 3 is plotted in Fig. 4. It shows that the output pulses with a higher modulation frequency (Figs. 4(d), 4(e), and 4(f)) feature a lower intensity of satellite pulses and therefore a better coherent contrast. Although the output spectrum for the higher modulation frequency in Fig. 3 seems quite clean, a tiny modulation still existed in the spectrum. The pedestals in Figs. 4(d), 4(e), and 4(f) were caused by the fine structure of the smoothed spectrum.

Fig. 4. (color online) Temporal coherent contrast of output for ((c), (f)) ; ((b), (e)) ; and ((a), (d)) . Panels (a), (b), and (c) were calculated for . was assumed for panels (d), (e), and (f).
3.3. Effects on spectral cleaning induced by FTL duration of input pulses

The influence of the input FTL pulse duration is plotted in Fig. 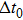5 and shows that pulses with a longer have a smoother output spectrum. The spectral cleaning effect can be strengthened by increasing the input FTL pulse duration. Since the second-order phase has a relatively low influence on pulses with long durations, the influence of the initial chirp on

Fig. 5. (color online) Output spectrum and corresponding temporal contrast for ((a), (b)) ; ((b), (e)) ; and ((c), (f)) . Here, , , and .

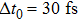
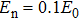
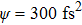
the output spectrum can be decreased by increasing the input FTL pulse duration. As concluded before, decreasing the initial chirp is beneficial in strengthening the spectral cleaning effect. Therefore, the XPW generation process appears to be an easy way to clean femtosecond pulses which have long pulse durations. The related temporal signals are plotted in Figs. 5(d), 5(e), and 5(f). It shows that for pulses with longer FTL pulse durations, the coherent contrast is improved.

4. Conclusion

In conclusion, the spectral cleaning effect of the XPW generation process was theoretically demonstrated and the underlying mechanism was investigated An analytical formula for the output spectrum was obtained. Through the investigation of the evolution of the spectral noise during the XPW generation process, it was found that the spectral cleaning effect strongly depends on the chirp and Fourier-transform-limited (FTL) duration of the input pulse and the modulation amplitude and frequency of the spectral noise. These factors codetermine the performance of the output spectrum, while the efficiency of the spectral cleaning effect is mainly constrained by the initial chirp. The study also shows that the smoothing of the spectrum in the XPW generation process leads to a significant enhancement of the coherent contrast.

Reference
[1] Umstadter D 2001 Phys. Plasmas 8 1774
[2] Murnane M Kapteyn H Falcone R 1989 Phys. Rev. Lett. 62 155
[3] Sebastian K Alexander S Jorg K Marco H Hartmut L Joachim H Malte C K 2016 Laser Photonics Rev. 10 264
[4] Minseok K Jinju K Vanessa L J P Hyyong S 2017 Opt. Express 25 14158
[5] Zhang C M Wang J L Li C Chen X W Leng Y X Lin L H Li R X Xu Z Z 2008 Chin. Phys. Lett. 7 2504
[6] Xu L Yu L H Chu Y X Gan Z B Liang X Y Li R X Xu Z Z 2015 Chin. Phys. 24 018704
[7] Wang J Z Huang Y S Xu Y Li Y Y Lu X M Leng Y X 2012 Acta Phys. Sin. 61 094214 in Chinese
[8] Ramirez L P Papadopoulos D Hanna M Pellegrina A Friebel F Georges P Druon F 2013 J. Opt. Soc. Am. 30 2607
[9] Marin L Amanda K M Michael G Charles G D 2015 Appl. Opt. 54 219
[10] Jullien A Kourtev S Albert O Cheriaux G Etchepare J Minkovski N Saltiel S M 2006 Appl. Phys. 84 409
[11] Xu Y Leng Y X Guo X Y Zou X Li Y Y Lu X M Wang C Liu Y Q Liang X Y Li R X Xu Z Z 2014 Opt. Commun. 313 175
[12] Zhang C M Giulio V Villeneuve D M Corkum P B 2015 J. Phys. B: At. Mol. Opt. Phys. 48 061001
[13] Hentschel M Kienberger R Spielmann C Reider G A Milosevic N Brabec T Corkum P Heinzmann U Drescher M Krausz F 2001 Nature 414 509
[14] Guenot D Gustas D Vernier A Beaurepaire B Bohle F Bocoum M Lozano M Jullien A Lopez-Martens R Lifschitz A Faure J 2017 Nat. Photonics. 11 293
[15] Schmid K Veisz L Tavella F Benavides S Tautz R Herrmann D Buck A Hidding B Marcinkevicius A Schramm U 2009 Phys. Rev. Lett. 102 124801
[16] Jullien A Chen X Ricci A Rousseau J P Lopez-Martens R Ramirez L Papadopoulos D Pellegrina A Druon F Georges P 2011 Appl. Phys. 102 769
[17] Ricci A Jullien A Rousseau J P Lopez-Martens R 2013 Appl. Sci. 3 314
[18] Jullien A Durfee C Trisorio A Canova L Rousseau J P Mercier B Antonucci L Cheriaux G Albert O Lopez-Martens R 2009 Appl. Phys. 96 293
[19] Ramirez L Papadopoulos D N Pellegrina A Georges P Druon F Monot P Ricci A Jullien A Chen X Rousseau J P 2011 Opt. Ex- press 19 93
[20] Dorrer C Bromage J Zuegel J 2008 Opt. Express 16 13534
[21] Osvay K Csatári M Ross I Persson A Wahlström C G 2005 Laser Part. Beams 23 327
[22] Diels J C Rudolph W 2006 Ultrashort laser pulse phenomena: fundamentals, techniques, and applications on a femtosecond time scale 2 New York Academic Press 21 26
[23] Schimpf D Seise E Limpert J Třnnermann A 2008 Opt. Express 16 8876
[24] Jullien A Canova L Albert O Boschetto D Antonucci L Cha Y H Rousseau J P Chaudet P Cheriaux G Etchepare J 2007 Appl. Phys. 87 595
[25] Canova L Albert O Forget N Mercier B Kourtev S Minkovski N Saltiel S M Martens R L 2008 Appl. Phys. 93 443