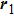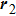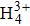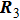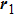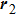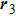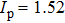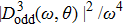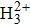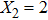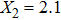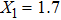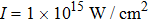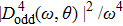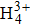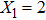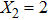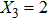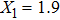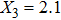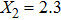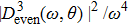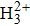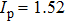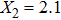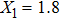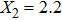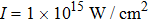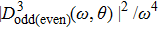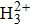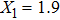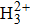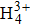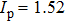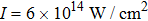† Corresponding author. E-mail:
We study high-order harmonic generation (HHG) from multi-center asymmetric linear molecules numerically and analytically. Our simulations show that odd and even HHG spectra of the asymmetric multi-center system respond differently to the change of the molecular structure. Specifically, when the internuclear distances between these nuclei of the molecule have a small change, the odd spectra usually do not change basically, but the even spectra differ remarkably. Based on this phenomenon, a simple procedure is proposed to probe the positions of these nuclei with odd–even HHG. Our results shed light on attosecond probing of the structure of multi-center molecules using HHG.
In the past two decades, high-order harmonic generation (HHG)[1,2] from atoms and molecules has been a hot subject in both experimental and theoretical studies of strong laser–matter interaction. This interest in HHG partly arises from the important applications of HHG in attosecond science,[3,4] including attosecond probing of the electron structure and dynamics.[5,6] The HHG process can be well understood by a semiclassical three-step model:[7] (i) ionization of the active electron by tunneling, (ii) propagation of the electron in the laser field, and (iii) recombination of the freed electron into the bound state with the emission of a high-energy photon.
Previous studies on HHG are mainly focused on atoms and diatomic molecules. For symmetric diatomic molecules, such as 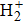
The odd–even HHG from asymmetric diatomic molecules has shown promising applications in ultrafast measurements. For instance, using odd–even HHG, one can probe the electron dynamics of asymmetric molecules,[52–56] image the asymmetric orbital,[43] and probe the nuclear dynamics of asymmetric molecules.[57] The degree of orientation for asymmetric molecules can also be calibrated with odd–even HHG.[58,59]
Recently, attention is increasingly turning to the interaction of the laser field with polyatomic molecules (such as CH4,[60–62] CH2Cl2,[63] C60,[64] and SF6[65]) and solids.[66–72] For symmetric polyatomic molecules such as CO2, the orbital symmetries can be complex with multiple nodal planes, and multielectron dynamics can become significant with several orbitals close to the highest occupied molecular orbital.[27] For asymmetric polyatomic molecules such as HCCl,[73] OCS,[50] and N2O,[74] due to symmetry breaking, the situation is more complex and some new effects can emerge. To probe the structure of multi-center asymmetric molecules with odd–even HHG, a detailed theoretical study on this issue is needed.
In this paper, we study odd–even HHG from multi-center asymmetric linear molecules 

The Hamiltonian of the molecular system studied here is 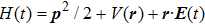



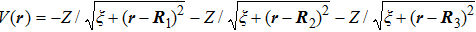
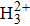
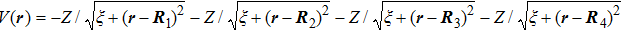
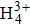

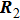
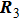
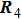
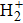
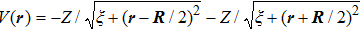

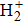
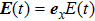
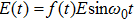


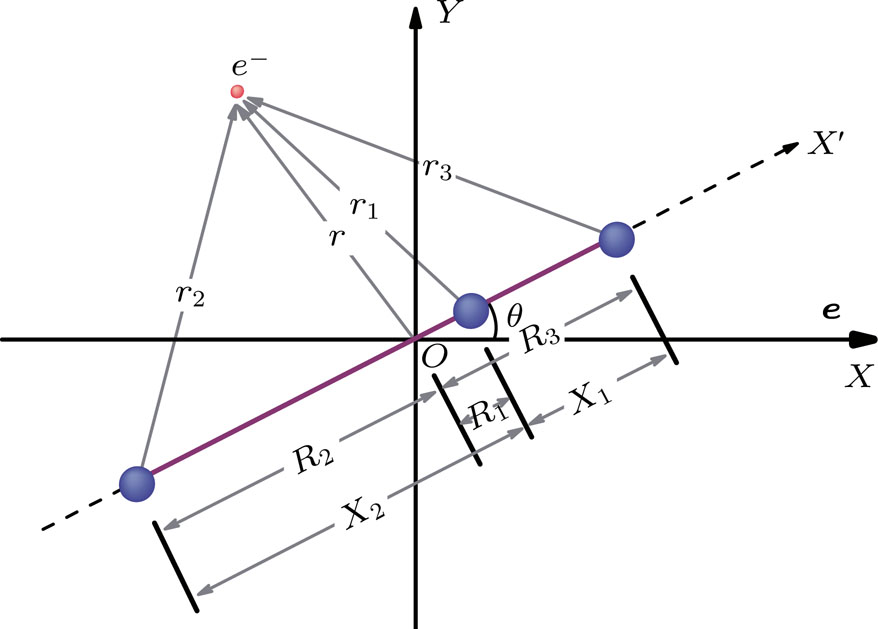
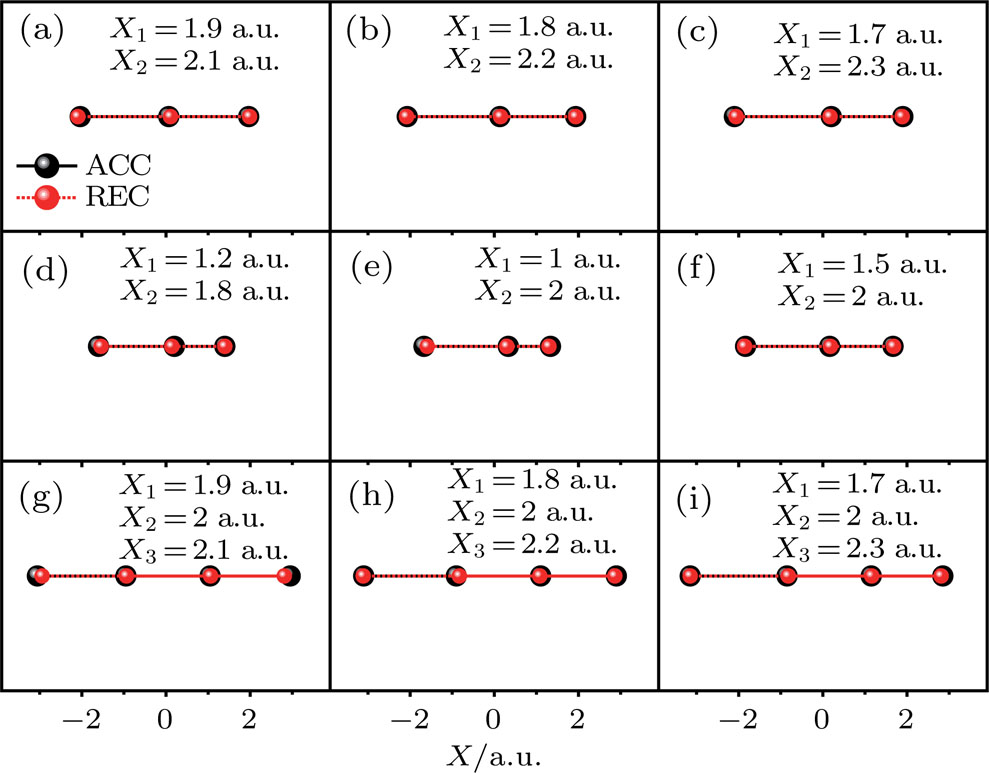
The sketches of the coordinate systems of 



 |
For comparison, the ground states of the linear molecules with different molecular parameters studied here have the same ionization potential of 
In Ref. [31], it has been shown that for asymmetric diatomic molecules, there is a close relation between odd–even HHG spectra and odd–even bound-continuum-transition dipoles. This relation reflects the main HHG route for the emission of one odd or even harmonic from asymmetric molecules.[43] The main odd (even) HHG route is associated with the rescattering electron ionizing from the gerade component of the asymmetric orbital and recombining with the gerade (ungerade) component of the asymmetric orbital. A detailed discussion on the odd–even HHG routes can be found in Refs. [32] and [54]. We now explore the relation for multi-center cases. For comparison, the diatomic cases are also discussed here.
We assume that the wave functions of the ground states 





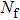
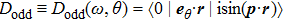

 |
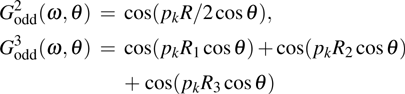 |
 |




 |
 |
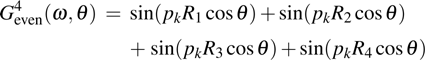 |


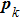
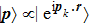


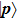
Note, due to the selection rule in the integral of the dipole, the odd dipole 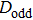



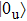
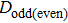

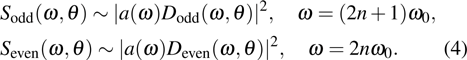 |

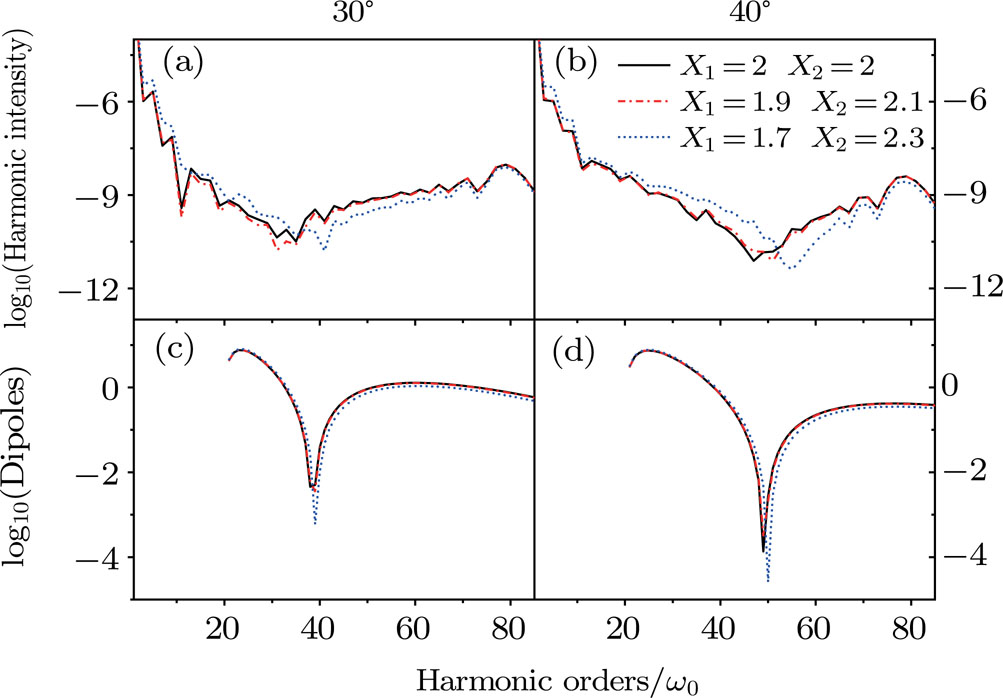
In Fig. 

In Figs. 




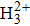

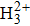

One can observe that the odd spectra in the first row of Fig. 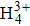
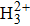
The results in Figs.
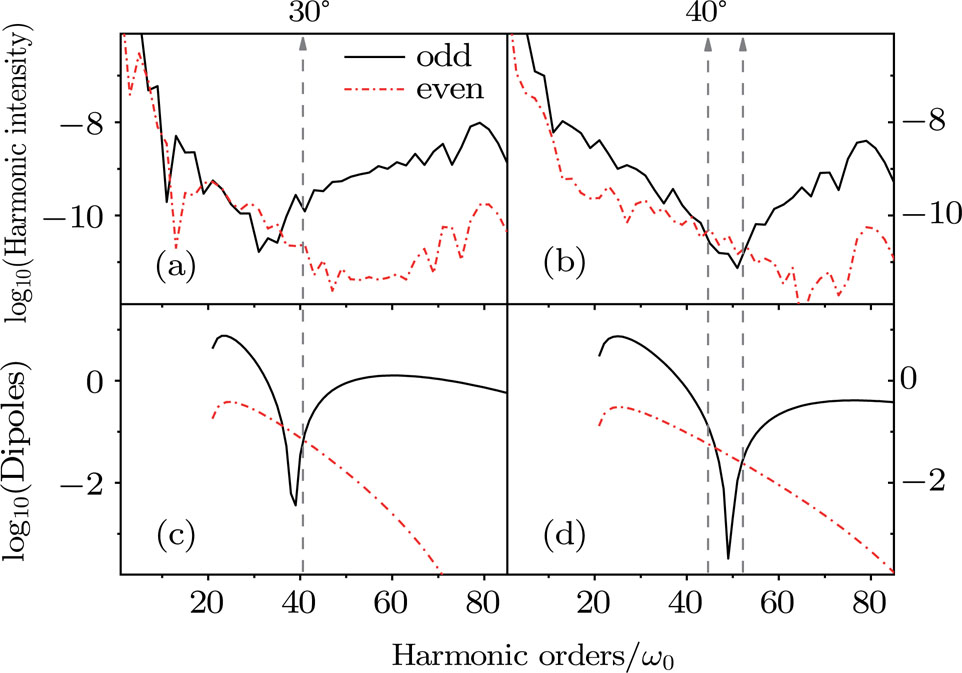
One of the important characteristics for the HHG from asymmetric molecules is the emission of even harmonics. Next, we turn to even spectra for multi-center asymmetric linear molecules. In Fig. 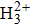

From the results in Figs.
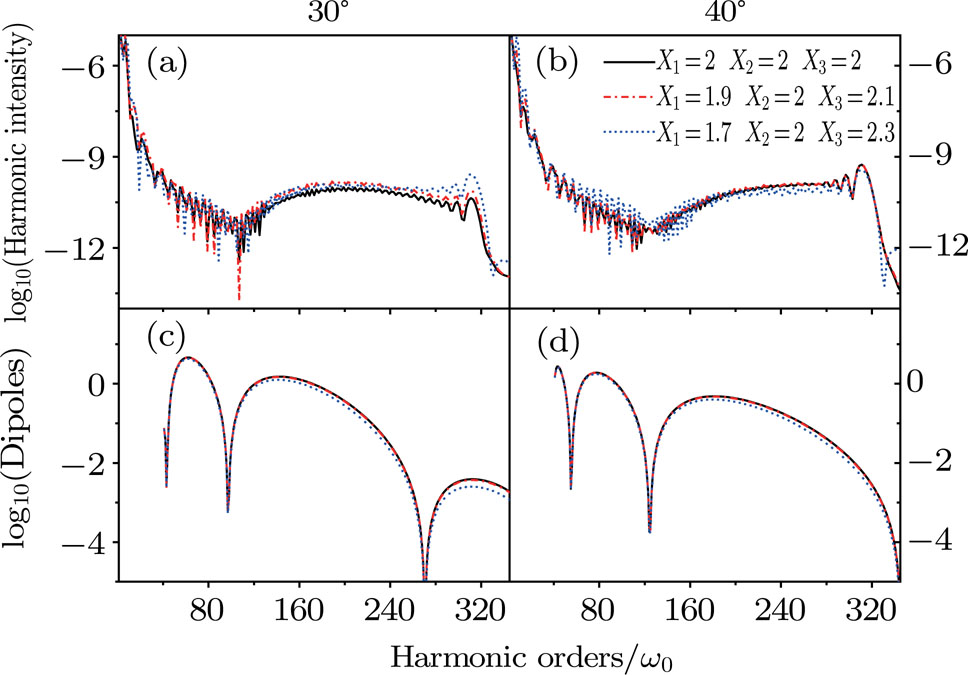
In Fig. 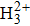

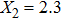
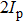
In Fig. 
It should be stressed that at smaller orientation angles, the intersections of odd–even HHG spectra are located at lower harmonic orders near the threshold, where the influence of the parent ions on the continuum electron is stronger. In this case, equation (
Here, all of the terms 
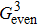
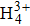
 |
In the first row of Fig. 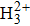

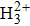



In summary, we have studied the HHG from multi-center asymmetric linear molecules 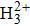


| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] | |
| [64] | |
| [65] | |
| [66] | |
| [67] | |
| [68] | |
| [69] | |
| [70] | |
| [71] | |
| [72] | |
| [73] | |
| [74] | |
| [75] | |
| [76] |