Polarization is an important characteristic of an electromagnetic (EM) wave and it must be taken into consideration in the practical application of the EM wave. In various wireless systems, such as mobile communications, radar tracking, satellite communications, and navigation systems, circularly polarized (CP) waves are preferred due to the advantages such as simplifying alignment and overcoming Faraday rotation.^[1] To generate a desired CP wave, in addition to the way to generate it directly by using CP antennas, an alternative effective way is to generate a linearly polarized (LP) wave and pass it through an LP-to-CP polarization converter. This way is particularly attractive in situations where the radiating system is a planar antenna array and generating CP waves at each element is not convenient. Moreover, one already designed LP antenna can be modified as a CP one by using a proper LP-to-CP polarization converter.

The polarization converter is a kind of polarization control device, which can convert an incident wave with a given polarization to a reflected or transmitted wave with a different polarization, it can be realized in different ways. Conventional polarization converters were usually designed by using the birefringence effect and optical activity of natural materials, which often suffer from bulky volumes, high losses, and narrow bandwidths in practical applications.^[2,3] Over the past decade, it has been found that metamaterials (MMs) can provide a convenient way to control the polarization state of an EM wave. Based on various MMs, many different polarization converters have been proposed.^[4–48] They were usually realized in one of the following two ways: one is to divide a wave into two orthogonal components and generate a phase difference between them (the fundamental of birefringence effect) by using anisotropic MMs, and the other one is to mimic the molecule chirality (the fundamental of optical activity) by using chiral MMs. The existing literatures indicate that the two methods can both be used to design various polarization converters, we can choose a proper design method according to the different work patterns of various polarization converters. Anisotropic two-dimensional MMs (also called metasurfaces) are more suitable for the design of reflective polarization converters, especially by using multiple plasmon resonances, high-efficiency and ultra-wideband polarization converters can be achieved in this way.^[4–15] For example, in Ref. [5], the authors presented a reflective polarization converter based on a double-V-shaped anisotropic metasurface, which can realize an ultra-wide band LP conversion due to four plasmon resonances, and another ultra-wideband polarization converter was proposed in Ref. [14], which is composed of three resonators. The chiral MM is convenient for designing transmissive polarization converters, and now most transmissive polarization converters are proposed based on various planar^[16–42] or 3D^[43–48] chiral MMs, which can realize linear^[16–29] or circular^[30–48] polarization conversion. In addition, due to the asymmetry of these chiral MM structures, in most cases, the asymmetric transmission effects, which means that the transmission coefficients are different for the incident waves with different polarizations (x/y- or RHCP/LHCP-polarizations), can also be observed at the same time.^{[16–29,32–48]} The asymmetric transmission effect can be used for polarization selection, it is very useful, however it should be avoided sometimes.

In this work, we propose an anisotropic metasurface, which is an orthotropic structure with a pair of mutually perpendicular symmetric axes u and v along directions with respect to the y-axis direction. The metasurface can realize wideband LP-to-CP polarization conversion at both x- and y-polarized incidences for the anisotropy; moreover, it has no asymmetric transmission effect, and its transmission coefficients at x- and y-polarized incidences are completely equal due to the symmetry. The simulated results show that its 3 dB axial ratio bandwidth is up to 40.4%, and the insertion loss can be kept below 1.31 dB over the entire band. In addition, the theoretical analysis shows that the orthotropy of the metasurface structure results in two independent transmission coefficients t_u and t_v at v- and u-polarized incidences; according to the difference between the two independent transmission coefficients, the polarization state of the transmitted wave can be completely determined.

The unit cell of the proposed metasurface consists of three conductive layers separated by two dielectric layers, as shown in Fig. 1. Each conductive layer contains a square loop aperture, however, in order to realize polarization-conversion, the square metal patch surrounded by the square loop aperture has been replaced by a corner-truncated one. The geometric shapes of the top and bottom conductive layers are completely the same, while that of the middle layer is a little smaller. After optimal selection, the geometrical parameters of the unit cell are chosen as follows: P = 6.00 mm, l_u = 5.65 mm, g_u = 0.63 mm, w_u = 3.80 mm, l_m = 5.10 mm, g_m = 0.60 mm, and w_m = 3.70 mm (see Fig. 1). In addition, these conductive layers are copper films with an electric conductivity and a thickness 0.017 mm, and the dielectric layers are selected as a Rogers RT/duroid 5880 substrate with a relative permittivity of 2.2 and a thickness of d = 2.00 mm.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. (color online) Unit cell of the proposed metasurface: (a) 3D view, (b) the top and bottom conductive layers, and (c) the middle conductive layer.

Owing to the orthotropy of the metasurface structure, when a common plane wave is incident on it, the transmitted wave would consist of both x- and y-polarized components, we invoke the transmission matrix to relate the complex amplitudes of the incident field to those of the transmitted field,

To numerically analyze the polarization conversion performance of our design, we suppose that the metasurface is located in the x–y plane, and a y-polarized wave with the magnitude of one unit is normally incident on it. As the simulated results using Ansoft HFSS, the magnitudes of cross- and co-polarized reflection and transmission coefficients, together with the phase difference , are shown in Fig. 2. In Fig. 2(a), it is indicated that the metasurface has a band-pass response in the frequency range from 12.2 GHz to 18.4 GHz, in which and are both close to 0.70, while and are both not large. Moreover, Figure 2(b) shows that the phase difference in this frequency band is close to −90°, it implies that the transmitted wave is close to an RHCP wave for it travels in the +z direction.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (color online) Simulated results of the proposed metasurface at y-polarized normal incidence: (a) the magnitudes of cross and co-polarized reflection and transmission coefficients; (b) the phase difference between the cross- and co-polarization transmission coefficients.

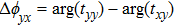
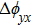
If the incident wave is assumed as a y-polarized one , according to formula (1), the transmitted electric field can be expressed as

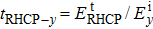
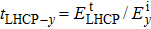
Based on the simulated results in Fig. 2(a), the two Y-to-CP transmission coefficients are calculated using formula (3), and the calculated results are shown in Fig. 3. It shows that the magnitude of the RHCP component is much greater than that of the LHCP component in the transmitted wave in the frequency range from 12.2 GHz to 18.4 GHz, and the y-polarized incident wave is almost converted to an RHCP one in this frequency band.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (color online) Y-to-CP transmission coefficients of the proposed metasurface at normal y-polarized incidence.

In fact, the transmitted wave is an elliptically polarized wave, we have calculated its axial ratio (AR) by using the following formula:

Fig. 4.

	Figure Option ViewDownloadNew Window
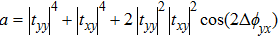
	Fig. 4. (color online) The total transmittance and the axial ratio AR of the proposed metasurface at y-polarized normal incidence.

The above-mentioned results are all obtained at the y-polarized incidence. In fact, as the simulated results using Ansoft HFSS, we have obtained the transmission coefficients at x-polarized incidence at the same time. It is shown that the metasurface does not have an asymmetric transmission effect, its reflection and transmission coefficients at the x- and y-polarized incidences are completely equal. It is just because the metasurface is a symmetric structure with a pair of mutually perpendicular symmetric axes u and v along directions with respect to the y-axis, as shown in Fig. 1(b), especially the symmetric axis u is just the angle bisector of the right angle between the positive x- and y-axes, which indicates that the x and y axes are mutually symmetrical in the metasurface structure, so , , and the same LP-to-CP polarization conversion can be realized at x- and y-polarized incidences.

In order to gain physical insight into the cause of the polarization conversion in the proposed metasurface, we present a detailed analysis.

The metasurface is symmetric with respect to both u and v axes, so no cross-polarized components will exist at u- and v-polarized incidences, and the two transmission coefficients can be expressed as t_u and t_v. The above-assumed y-polarized incident wave can be considered as a composite wave consisting of both u- and v-polarized components, moreover, the magnitudes of the two polarized components are exactly equal, thus the incident and transmitted waves can be respectively expressed as

Due to the orthotropy of the metasurface structure, t_u and t_v are mutually independent. In order to facilitate the derivation of the formula, we define the magnitude ratio between t_u and as , in addition, the phase difference between them is . Formula (6) implies that the moving track of the tip of the transmitted electric field vector on any fixed plane in parallel to the u–v one, which is normal to the direction of propagation, will satisfy the elliptic equation

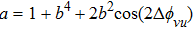
In the x–y coordinate system, by using the relationships and , equation (7) can be derived as

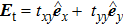
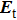
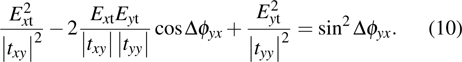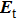
Formulas (11)–(13) indicate that we can obtain the magnitudes of cross- and co-polarization transmission coefficients t_xy and t_yy, together with the phase difference , at the y-polarized incidence by using the two independent transmission coefficients t_u and t_v at u- and v-polarized incidences. In addition, formula (8) shows that the polarization state of the transmitted wave can be determined by using the magnitude ratio b and phase difference . In common cases, b and maybe both are an arbitrary value, the transmitted wave would be elliptically polarized; when b = 1 and , the anticipated LP to CP polarization conversion will be realized; if b = 1 and , then no polarization conversion exists, however, this will not happen if the proposed metasurface is an anisotropic structure.

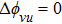
To validate the polarization conversion performance of the proposed metasurface by using formula (8), we carry out numerical simulations at u- and v-polarized incidences, respectively. The simulated results in Fig. 5(a) indicate that the magnitudes of t_u and t_v are both much closer to 1.0 in the frequency range from 12.2 GHz to 18.4 GHz. In addition, Figure 5(b) shows that the phase difference is close to −90° in this frequency range. It implies that the two transmitted components at the two equal u- and v-polarized incidences will be combined into a CP wave in this frequency band. We have calculated the AR of the total transmitted wave by using formula (8), the calculated results, shown in Fig. 5(c), indicate that the results obtained at the u- and v-polarized incidences are almost the same as those obtained at the y-polarized incidence shown in Fig. 4.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. (color online) Simulated results of the proposed metasurface at u-polarized and v-polarized incidences: (a) the magnitudes of tu and tv; (b) the phase difference between tu and tv, and (c) the axial ratio AR of the total transmitted wave.

Moreover, to validate formulas (11)–(13), according to the simulated results in Figs. 5(a) and 5(b), the magnitudes of t_yy and t_xy, together with the phase difference , are calculated by using formulas (11)–(13). Figure 6 shows that the calculated results are almost in agreement with the simulated results at y-polarized incidence in Fig. 2.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. (color online) The comparison between the calculated and simulated results at y-polarized incidences: (a) the magnitudes of tyy and txy; (b) the phase difference between tyy and txy.

From the above analysis, we can conclude that the orthotropy of the metasurface structure has resulted in two independent transmission coefficients t_u and t_v; according to the two independent transmission coefficients t_u and t_v, the total transmission properties of the metasurface can be determined completely; however, to determine the polarization state of the transmitted wave, only the difference between t_u and t_v (the magnitude ratio b and phase difference is needed; when their difference is appropriate (b = 1, , the anticipated LP to CP polarization conversion will be realized; if there is no difference between them (b = 1 and , then no polarization conversion will occur, it indicates that the orthotropy of the metasurface structure is the root cause of the polarization conversion.

Finally, to realize an experimental validation for our design, one prototype of the proposed metasurface was fabricated by using the standard PCB lithography and substrate bonding technique, which consists of 42×42 unit cells with an area of 252 mm×252 mm, as shown in Fig. 7(a). We have carried out an experiment in a microwave anechoic chamber, and the transmission coefficients of the metasurface at y-, u-, and v-polarized incidences were all measured by using a pair of transmitting and receiving horn antennas, which were connected to the two ports of a vector network analyzer (VNA), as shown in Fig. 7(b). As the measured results, the magnitudes of the transmission coefficients t_yy, t_xy, and t_u, t_v are shown in Figs. 7(c) and 7(d), respectively, and the phase differences and are both shown in Fig. 7(e). Compared with the simulated results, good agreements can be observed for all of the measured results. Finally, according to these measured results, we have obtained the axial ratio ARby using formulas (4) and (8) successively. The calculated results, together with the simulated results, are shown in Fig. 7(f). They indicate that the experiment results obtained at y-polarized incidence are basically the same as those obtained at u- and v-polarized incidences, they are both in agreement with the numerical predication, however, there still is a small deviation between them, this could be caused by experimental errors because the size of the experimental sample is very limited and the effective size will be more limited at u- and v-polarized incidences.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. (color online) (a) Photograph of the fabricated prototype. (b) Schematic diagram of the experimental setup. The comparison between the experiment and simulated results: (c) the magnitudes of tyy and txy; (d) the magnitudes of tu and tv; (e) the phase differences and , and (f) the axial ratio AR of the total transmitted wave.

This work presents an anisotropic metasurface, which is symmetric with respect to the u and v axes. Numerical simulated results show that the metasurface can realize wideband LP-to-CP polarization conversion; moreover, its transmission coefficients at x- and y-polarized incidences are completely equal. Furthermore, we analyze the cause of the polarization conversion, and conclude that the metasurface has two independent transmission coefficients t_u and t_v, which results from the orthotropy of the metasurface structure; according to the two independent transmission coefficients t_u and t_v, the total transmission properties of the metasurface can completely be determined. Finally, we have carried out an experiment in which the polarization conversion performance of the proposed metasurface, together with some effective conclusions, has been confirmed effectively. Compared with the previous designs, the proposed metasurface, as a novel LP-to-CP polarization converter, has wider bandwidth. At the same time, it has no asymmetric transmission effect, so it is of great application value in polarization control devices, stealth surfaces, antennas, etc.