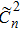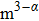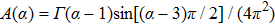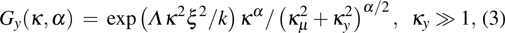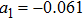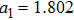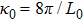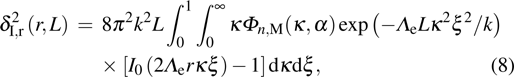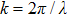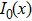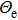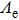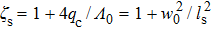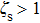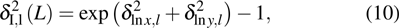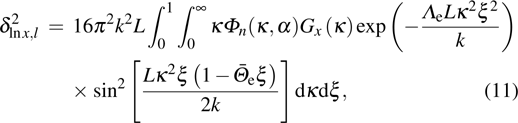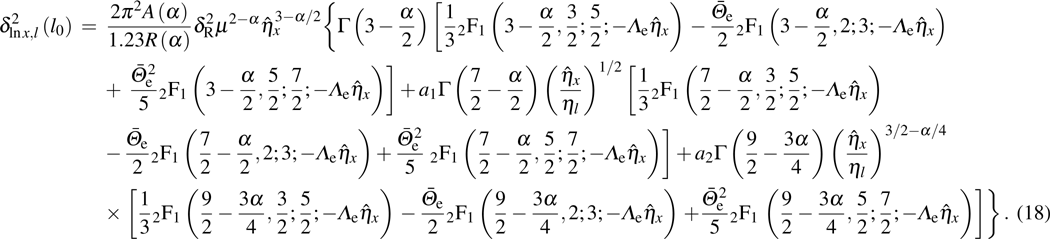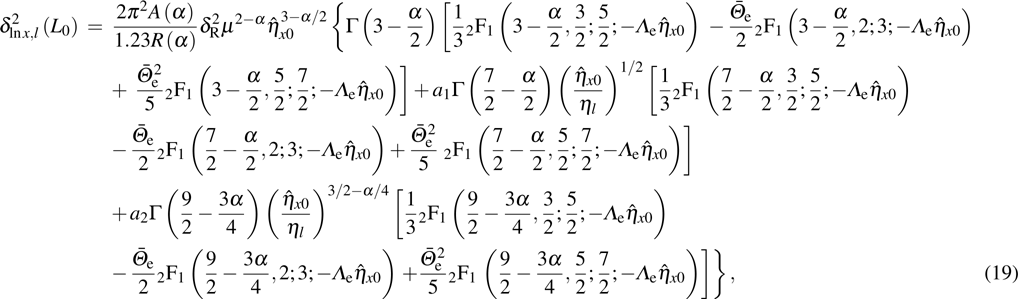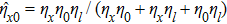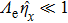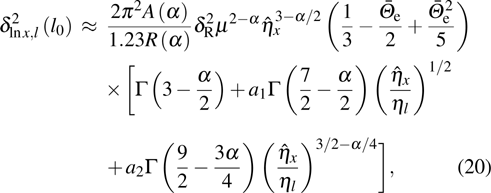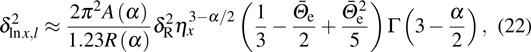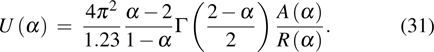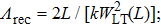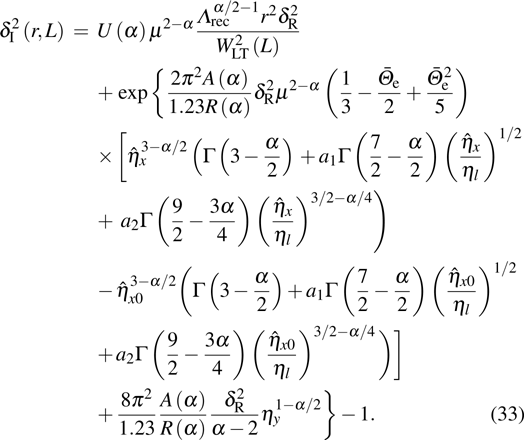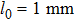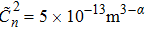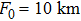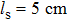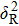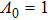Influence of moderate-to-strong anisotropic non-Kolmogorov turbulence on intensity fluctuations of a Gaussian–Schell model beam in marine atmosphere
1. IntroductionResearch on the propagation behavior of laser beams through atmospheric turbulence is of significant importance in various applications, including free-space optical (FSO) communications, imaging systems, and remote sensing.[1] Atmospheric turbulence produces several negative effects that can severely degrade these systems’ performance, of which the most noticeable is the intensity fluctuation, known as scintillation.[2] To mitigate these turbulence effects, considerable effort has been put into partially coherent beams.[3,4] Both theory and experiment show that partially coherent beams have a significant advantage over fully coherent ones in mitigating turbulence-induced scintillation.[5,6] The Gaussian–Schell model (GSM) beam is an important member of the partially coherent beams, whose amplitude distribution and spatial coherence function are both Gaussian shapes. It can be easily generated by passing through the phase diffusers at the laser transmitter. Over the past decades, the irradiance scintillation index (SI) for Gaussian beams under weak and moderate-to-strong turbulence regimes has been developed,[7–12] and employed to examine the performance of FSO communication systems based on GSM beams.[13–15] However, these studies mainly focused on the isotropic Kolmogorov or non-Kolmogorov terrestrial atmospheric turbulence.
With increasing activities and communication needs in the marine environment, it is essential to understand the turbulent effects in the marine atmosphere. The SI of a laser beam in a marine atmosphere is relatively less explored compared to that in a terrestrial atmosphere. In the marine atmosphere, large bodies of water act differently from soils,[16] which makes the marine atmospheric turbulence behave differently from the terrestrial atmospheric turbulence. The statistical models derived for terrestrial atmospheric turbulence cannot be applied directly to marine atmospheric turbulence. A new power spectrum of marine atmospheric turbulence was proposed and used to develop the SI models for plane waves, spherical waves, and higher-order laser beams in a weak Kolmogorov turbulent marine atmosphere.[17–19] The non-Kolmogorov marine atmospheric turbulence spectrum has been adopted to analyze the SI of a Gaussian beam in a weak marine atmospheric turbulence.[20] Due to the sea surface friction on the air motion, optical turbulence in a marine atmosphere can be anisotropic. The polarization, beam wander, and spreading of Gaussian–Schell model beams propagating in an anisotropic non-Kolmogorov turbulent marine atmosphere were investigated.[21,22] In 2016, Cui developed the SI of Gaussian beams through weak anisotropic non-Kolmogorov turbulence.[23] To the best of our knowledge, the SI of partially coherent GSM beams in moderate-to-strong anisotropic non-Kolmogorov marine atmospheric turbulence has never been examined.
In this paper, the on-axis and off-axis SIs of a GSM beam through a moderate-to-strong anisotropic non-Kolmogorov marine atmosphere are developed by adopting the extended Rytov theory. The influences of the anisotropy coefficient, power-spectrum index, turbulence inner-, outer-scales, turbulence structure parameter, off-axis distance, propagation distance, spatial correlation length, wavelength, and beam width on the SIs of GSM beams are discussed in detail.
2. TheoryBased on the extended Rytov theory, the effective anisotropic non-Kolmogorov modified atmospheric spectrum model can be expressed as[11]
where

represents the anisotropic non-Kolmogorov spectrum over the inertial sub-range
[24]where
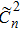
is the generalized refractive-index structure parameter with units
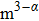
,
μ denotes the anisotropy coefficient,
α is the power-spectrum index,

is a constant that maintains consistency between the refractive-index structure function and its power spectrum that has the form
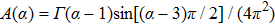
with symbol

being the Gamma function.
[25] When
α =11/3 and
μ =1, equation (
2) reduces to the standard Kolmogorov spectrum model.
The high-pass filter function of small-scale
 and low-pass filter function of large-scale
and low-pass filter function of large-scale
 can be written as
can be written as
where

. In the marine atmosphere,
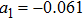
,

, and in terrestrial atmosphere,
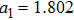
,

. Specifically, the parameter

is a large-scale (or refractive) cutoff spatial frequency for the large-scale turbulent cells, and

is a small-scale (or diffractive) cutoff spatial frequency for the small-scale turbulent cells.

,
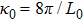
,
l0, and
L0 are turbulence inner-scale and outer-scale; parameter
c0 has the form of
[20]
The total SI of a GSM beam propagation in the turbulent atmosphere is composed of radial (off-axis) and longitudinal (on-axis) components[2]
where
where
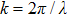
is the wavenumber with
λ being wavelength,
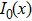
is a modified Bessel function of the first kind;
L is the propagation distance,
ξ is the normalized path coordinate and related to
z by
 r
r is the off-axis parameter; the complementary parameter

s,
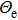
and
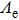
, are effective output beam parameters of GSM beams, that are related to the input beam parameters

and

of Gaussian beams
[2]where

and

are defined by

and

, respectively. Here,
F and
w0 denote the phase front radius of curvature and beam radius at the input plane, respectively.
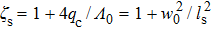
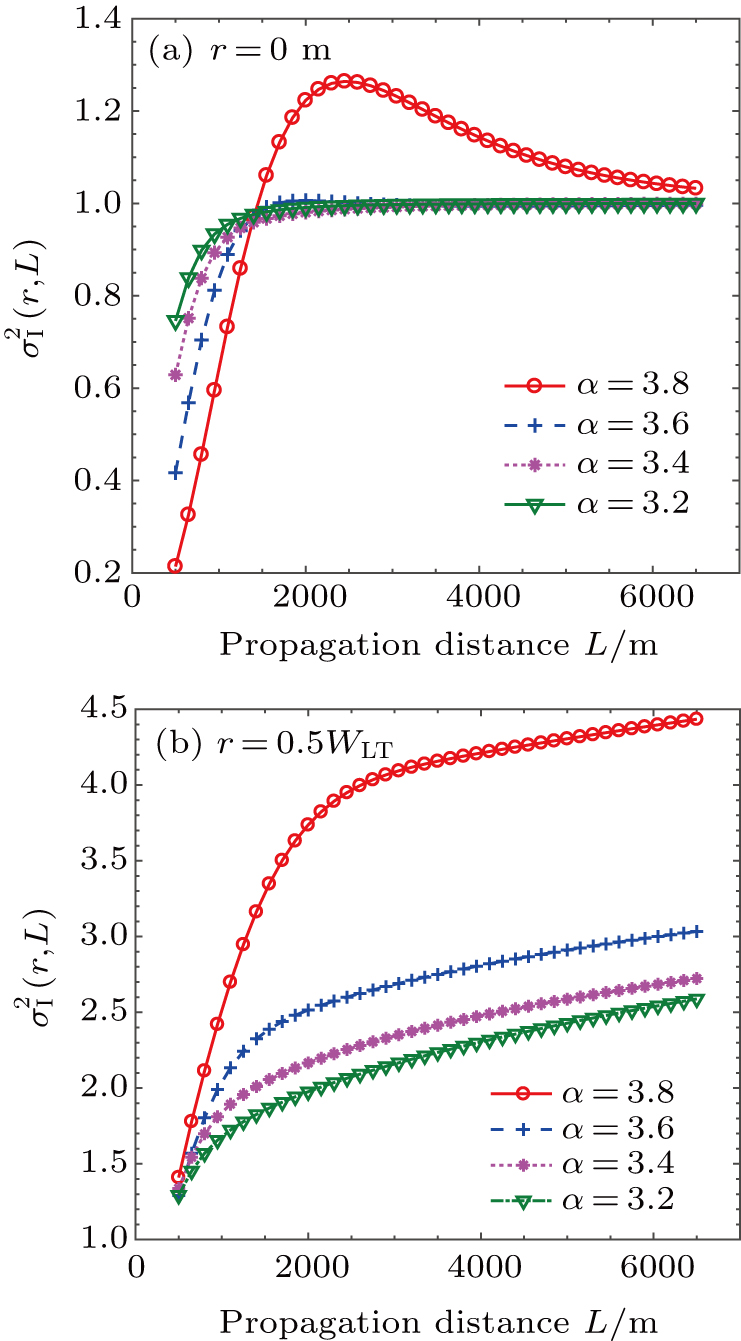
is the source coherence parameter of the GSM beam (if

, the beam is fully coherent, if
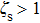
, the beam is partially coherent), and
ls is the partial coherence length, which describes the partial coherence properties of the source.
The on-axis SI of GSM beam propagation in moderate-to-strong anisotropic non-Kolmogorov turbulence takes the following form:
where

and

are large-scale and small-scale log-irradiance on-axis SIs of GSM beams, respectively, and given by
For large-scale log-irradiance on-axis SI, we use the geometrical optics approximation of sin
 , equation (11) can be expressed as the difference, viz.,
, equation (11) can be expressed as the difference, viz.,
where
where
is the SI of a plane wave in weak non-Kolmogorov turbulence,

,

,

,

.
Based on the integrals,[26]
and
equation (
14) becomes
Analogously, equation (15) can be expressed as
where
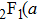
,
b;
c;

is a hypergeometric function,
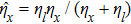
and
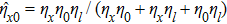
. When
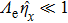
, all the above hypergeometric functions are approximately equal to one, thus equations (
18) and (
19) reduce to
Note that when
 ,
,
 ,
,
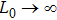 , equation (13) reduces to
, equation (13) reduces to
which is the large-scale log-irradiance on-axis SI for the zero-scale case in the isotropic turbulent atmosphere.
[11]Along the same lines, we adopt the approximation of
 for the small-scale log-irradiance on-axis SI
for the small-scale log-irradiance on-axis SI
 , and equation (12) can be written as
, and equation (12) can be written as
where

.
Similar to Ref. [11], the large-scale and small-scale parameters can be calculated as
where

is the SI of GSM beam wave in weak anisotropic turbulence and is related to that in weak isotropic turbulence
[20]where
The off-axis SI for an untracked GSM beam in moderate-to-strong anisotropic non-Kolmogorov turbulence[11] is given by
Considering additional beam wander and diffraction effects, the effective beam parameters are adopted by
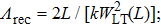
 is the long-term spot size for the GSM beam through anisotropic non-Kolmogorov turbulent atmosphere[22]
is the long-term spot size for the GSM beam through anisotropic non-Kolmogorov turbulent atmosphere[22]
Based on equations (20), (21), and (30), the total SI of partially coherent GSM beams propagating through moderate-to-strong marine or terrestrial atmospheric turbulence can be expressed as
3. Numerical discussionIn this section, the numerical results of the SIs for partially coherent GSM beams propagating in a moderate-to-strong anisotropic non-Kolmogorov turbulent marine atmosphere are discussed. The following parameter values are assumed unless otherwise specified: anisotropy coefficient μ = 1.2, power-spectrum index α =3.8, turbulence inner-scale
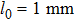 , and outer-scale
, and outer-scale
 , turbulence structure parameter
, turbulence structure parameter
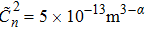 , propagation distance L = 4 km, wavelength
, propagation distance L = 4 km, wavelength
 , beam width
, beam width
 , phase curvature parameter
, phase curvature parameter
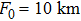 , and spatial correlation length
, and spatial correlation length
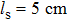 .
.
Figure 1 shows the dependence of the on-axis (Fig. 1(a)) and off-axis (Fig. 1(b)) SIs of GSM beams through anisotropic non-Kolmogorov turbulence with source spatial coherence length ls. A comparison of results in the marine and terrestrial atmosphere is also presented in Fig. 1. Both the on-axis and off-axis SIs for GSM beams are sensitive to the changes in ls, and the negative effect of the turbulence on GSM beams can be reduced by decreasing the value of ls. Partially coherent beams showed an obvious advantage over fully coherent ones in lowering the turbulence-induced SI. The on-axis SI in a turbulent marine atmosphere is higher than that in a turbulent terrestrial atmosphere. The result of the off-axis SI is different from that of the on-axis SI: terrestrial atmosphere produces a larger effect on the off-axis SI than the marine atmosphere.
The impact of the anisotropy coefficient μ (μ = 1, 1.1, 1.2, and 1.3) on the on-axis (Fig. 2(a)) and off-axis (Fig. 2(b)) SIs of GSM beams in an anisotropic non-Kolmogorov marine atmosphere is investigated in Fig. 2. The on-axis SI of GSM beams increases with the turbulence strength until it reaches a maximum value in the focusing regime, where large-scale inhomogeneity achieves its strongest effect; the on-axis SI enters the saturation decreasing regimes after reaching a maximum value because the focusing effect is weakened by multiple scattering in the turbulent saturation region. Atmospheric spatial coherence increases as the anisotropy parameter μ increases; the increase in μ leads to turbulent eddies acting as lenses with longer radii of curvature. A beam passing through an anisotropic turbulent eddy is less deviated from the direction of propagation and has a narrow spot size.[24] The point of large off-axis SI is closer to the beam center in anisotropic turbulence than that in isotropic turbulence. At a fixed position, the anisotropy characteristic of atmospheric turbulence leads to the decline in the on-axis SI and the rise in the off-axis SI. This effect is obvious in the moderate fluctuation regions for the on-axis SI, whereas for the off-axis SI, it is obvious at the positions far from the beam center.
Figure 3 depicts the influences of turbulence inner-scale l0 and outer-scale L0 on the on-axis SIs of GSM beams as a function of propagation distance L in an anisotropic non-Kolmogorov marine atmospheric turbulence. The curves of the on-axis SIs for different l0 and L0 values follow similar trends, but different values are obtained. Turbulence inner-scale has an important effect on the on-axis SIs in moderate fluctuation regions. Turbulence outer-scale plays a more important role in determining the strength of the on-axis SI in strong-turbulence regions. Both the turbulence inner-scale and outer-scale effects should be considered in the evaluation of the SI when the beam propagates in moderate-to-strong atmospheric turbulence.
Figure 4 illustrates the importance of wavelength λ on the on-axis SIs of GSM beams through an anisotropic non-Kolmogorov marine turbulent atmosphere as a function of L for λ = 1550, 1024, 850, and 632.8 nm. In weak-to-moderate turbulence regime, the on-axis SI increases with the decrease of λ; it trends toward a steady value when entering into the turbulence saturation phase. Wavelength also has a significant effect on the distance from the point (at which the maximum value is obtaining) to the source plane, a decreasing value of λ leads to a short distance.
Figure 5 shows a plot of the total SIs of GSM beams in an anisotropic non-Kolmogorov marine turbulent atmosphere versus input beam parameter
 from 10−1 to 103 at a fixed propagation distance L = 1 km, where the effects of different values of the off-axis parameter r are considered. With the increase of
from 10−1 to 103 at a fixed propagation distance L = 1 km, where the effects of different values of the off-axis parameter r are considered. With the increase of
 , the on-axis SI first decreases down to a trough and then begins to increase again. The curves of the off-axis SIs are different from the case of the on-axis SIs, which increase steeply to a peak value, and then decrease to zero. As
, the on-axis SI first decreases down to a trough and then begins to increase again. The curves of the off-axis SIs are different from the case of the on-axis SIs, which increase steeply to a peak value, and then decrease to zero. As
 , GSM beams tend to be spherical waves, the on-axis SI of GSM beams is approximately equal to that of the spherical wave, and the off-axis SI disappears. The off-axis parameter r has a significant effect on the SIs of GSM beams in the vicinity of
, GSM beams tend to be spherical waves, the on-axis SI of GSM beams is approximately equal to that of the spherical wave, and the off-axis SI disappears. The off-axis parameter r has a significant effect on the SIs of GSM beams in the vicinity of
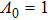 in a marine atmosphere.
in a marine atmosphere.
Figure 6 exhibits the effect of power-spectrum index α on the SIs of GSM beams for α = 3.2, 3.4, 3.6 to 3.8 in an anisotropic non-Kolmogorov marine turbulent atmosphere. The on-axis SI increases with the decrease of α in the moderate-turbulence regime, which is consistent with the results in the weak turbulence regime.[20] whereas the on-axis SI enters into the turbulence saturation regime after reaching a maximum value, α has an opposite effect on it. Different values of α lead to obvious variations in the SIs which are away from the beam center.
4. ConclusionIn conclusion, we have quantitatively investigated the SIs of GSM beams in a moderate-to-strong anisotropic non-Kolmogorov turbulent atmosphere. Both the on-axis and off-axis SIs of GSM beams in the turbulence were sensitive to changes in spatial correlation length; partially coherent beams showed an advantage over fully coherent ones in lowering the turbulence-induced SI. The on-axis SI in the marine atmosphere was higher than that in the terrestrial atmosphere, but the off-axis SI exhibited the opposite result. The anisotropy characteristic of turbulence led to a decline in the on-axis SI and a rise in the off-axis SI. Turbulence inner-scale had an obvious influence on the on-axis SI in moderate fluctuation regions, but the outer-scale effect was more apparent in strong-turbulence regions. The decrease in the on-axis SI induced by wavelength was remarkable in the moderate-to-strong. The on-axis SI initially increased with the turbulence strength, then began to decrease after reaching a maximum value. The on-axis SI increased with the decreasing power-spectrum index in the moderate-turbulence regime; it had the reverse effect in the saturation regime. The off-axis SIs strengthened as the off-axis parameter and propagation distance increased. With the increase in beam parameter
 , the on-axis SI first decreased to a trough, and then began to increase again; the result of off-axis SI was opposite to that of the on-axis SI.
, the on-axis SI first decreased to a trough, and then began to increase again; the result of off-axis SI was opposite to that of the on-axis SI.