† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11775083 and 11374108), the National Training Program of Innovation and Entrepreneurship for Undergraduates, China, and Special Funds for the Cultivation of Guangdong College Students’ Scientific and Technological Innovation, China (Grant No. pdjh2017b0137).
The propagation dynamics of a chirped Airy vortex (CAiV) beam with x-polarization in uniaxial crystals orthogonal to the optical axis is studied analytically and numerically. The effect of the ratio of extraordinary and ordinary refractive indices, the chirp parameter, as well as the propagation distance is analyzed, which shows that the focused position of the CAiV beams can be controlled through changing the ratio of the extraordinary and ordinary refractive indices. In addition, with the propagation distance increasing, the asymmetry of the intensity and the angular momentum of the CAiV beam during propagation becomes much more visible. The variation of the chirp parameters can change the attenuation velocity of the vortex as well.
Ever since Airy wave packets, which are a solution of the Schrödinger equation in the background of quantum mechanics, were first discovered by Berry[1], research on these beams has advanced rapidly. The Airy beam can heal itself after being obscured by an obstacle.[2] What is more, these beams have a self-bending property as well as acceleration.[3] In practice, single solitons and soliton pairs can be produced during the interactions of similar Airy beams and nonlinear accelerating beams through Kerr and saturable nonlinear media.[4,5] In addition, the optical vortex is gradually noticed.[6] A vortex beam is a laser beam which contains a continuous spiral phase distribution.[7] Subsequently, the propagation dynamics of Airy vortex (AiV) beams, Airy Gaussian vortex (AiGV) beams and circular Airy vortex beams have been explored theoretically and experimentally.[8–10] In this paper, we add the chirp parameter on the basis of the AiV beams. Chirp is a phenomenon in which the signal changes frequently over time, the frequency spectrum will be widened before and after the pulse due to modulation.[11] The chirp has been applied for phase modulation when the beams propagate in different media.[12] The chirp parameter is used to describe this phenomenon.
Different from other isotropic medium, the uniaxial crystal is an anisotropic material that has unusual peculiarities.[13] Uniaxial crystal is always used in the design of optical devices because of its anisotropy impacting the polarization of light. In 2008, Deng et al. analyzed the propagation properties of hollow beams in uniaxial crystals, and they discovered that the symmetry of the beams was no longer maintained in the uniaxial crystals.[14] It is really interesting to analyze the propagation dynamics of light through anisotropic media in both applied and theoretical optics. The propagation properties of elliptical Gaussian beams, Airy–Hermite–Gaussian beams, Airy beams, Laguerre–Gaussian beams, Bessel–Gaussian beams and flattened-Gaussian beams in uniaxial crystals have been studied.[15–19] While the propagation of CAiV beams through uniaxial crystals has not been reported.
In the Cartesian coordinate system, the propagation axis is set as the z axis, and the x axis is taken to be the optical axis of the uniaxial crystal. The input plane is at z = 0 and the observation plane is taken to be z. The dielectric tensor of the uniaxial crystal is depicted as[20]
 |
The initial electric field distribution of the CAiV beam with x-polarization is
 |
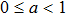


 |
The paraxial transmission of CAiV beams with x-polarization through uniaxial crystals can be described by
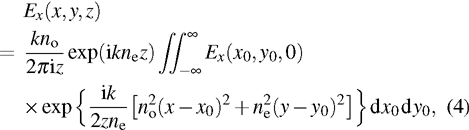 |
The analytical complex field distribution of CAiV beams with x-polarization through uniaxial crystals at distance z can be formulated as
 |
 |
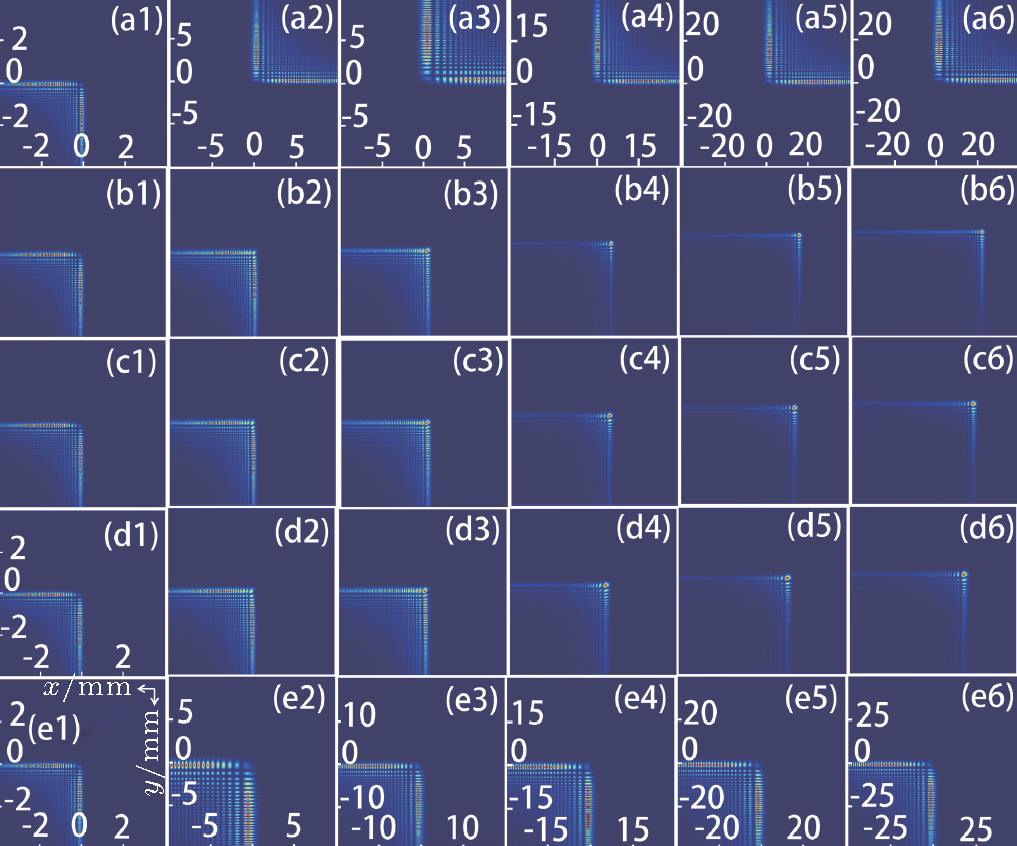
In order to illuminate the features of CAiV beams with x-polarization through uniaxial crystals more clearly, we investigate the trajectories with different ratios of ne (the extraordinary index) and no (the ordinary index) as well as the intensity and the phase distributions at different distances with different chirp parameters.
Figure 
 | Fig. 1. (color online) Propagation dynamics of CAiV beams as a function of distance when (a) 



|
Figure
 | Fig. 2. (color online) The maximum intensity of the CAiV beams as a function of propagation distance. |
To discuss the effect of the chirp parameter C, we take a = b = 0.01, no = 2.616, ne = 3.1392, 
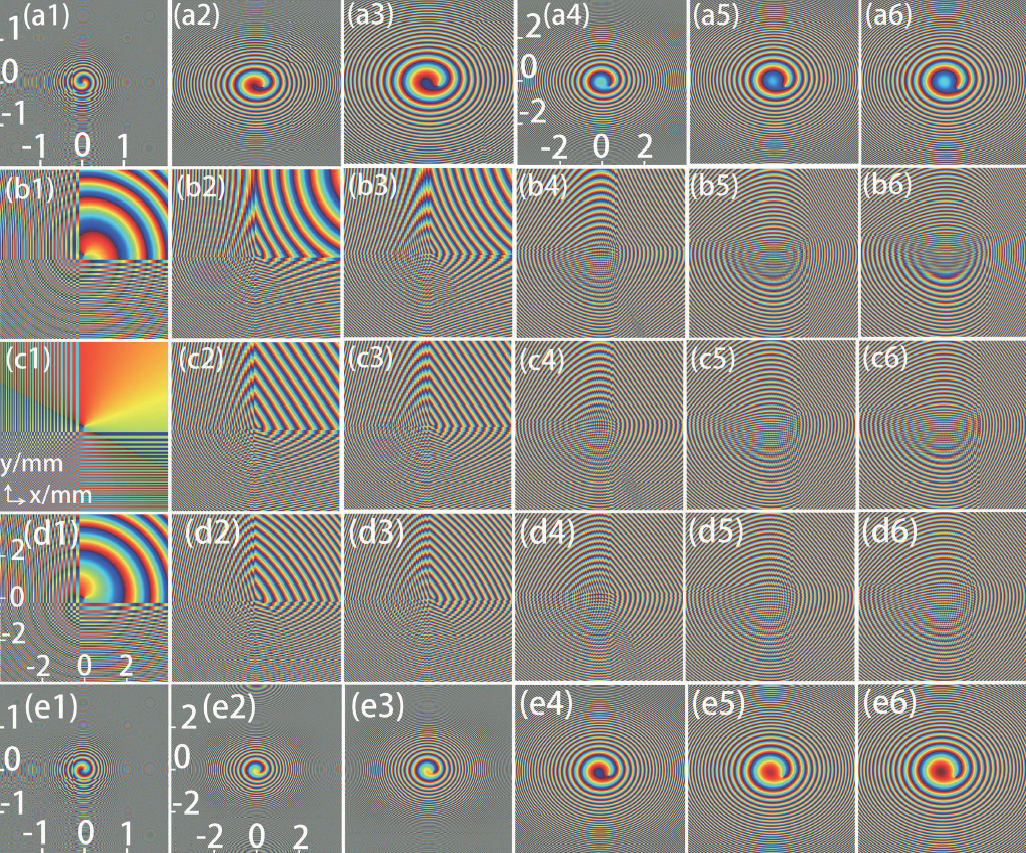 | Fig. 4. (color online) The phase distribution of the CAiV beams. All the parameters are the same as those in Fig. |
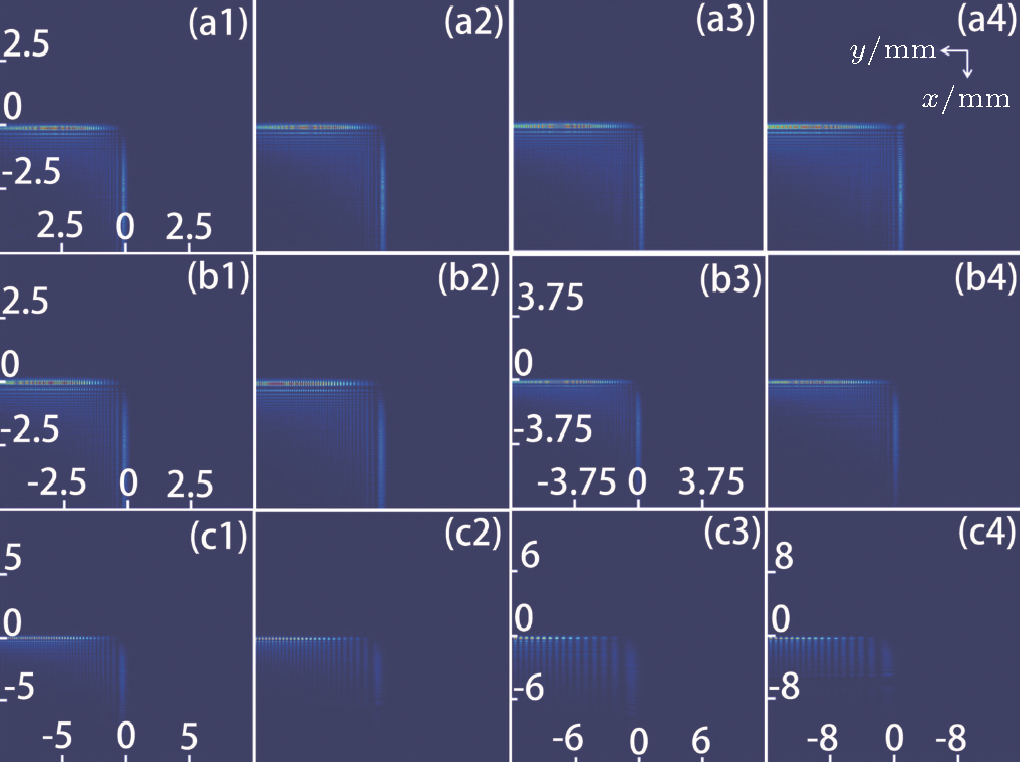
To further analyze the influences of the chirp parameters and the distribution factors, we plot Fig. 
Figure
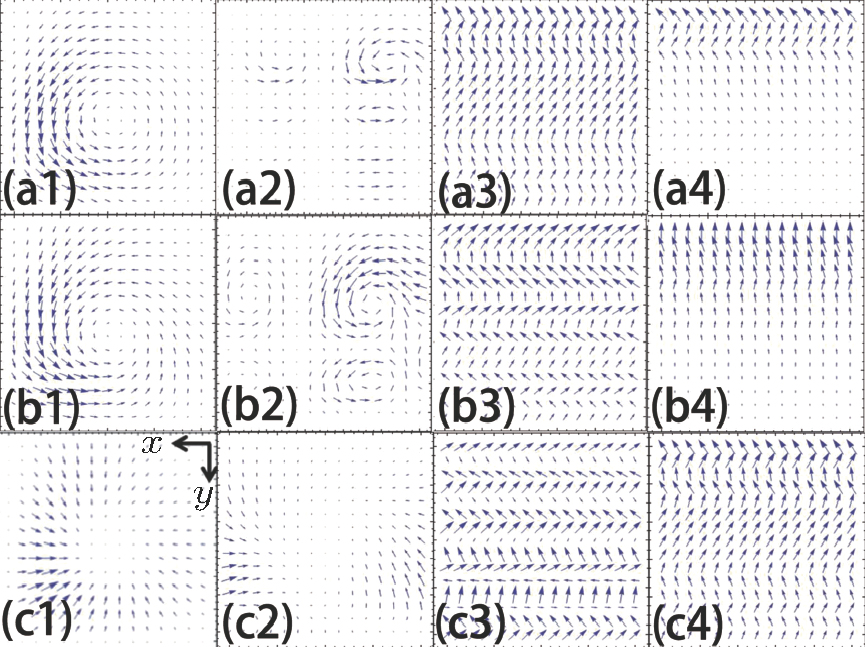
To analyze the propagation properties of the CAiV beams with x-polarization through uniaxial crystals, we calculate the Poynting vector. We use the Poynting vector to illustrate the propagation dynamics of the CAiV beams. The Poyting vector can be expressed as 

 |
 |
 |
On the other hand, with different chirp parameters, the distributions of the vortex are different. It is clearly seen that, as the chirp parameter increases, the attenuation velocity of the vortex becomes slower.
The angular momentum plays an important part in electromagnetism.[25] The time-averaged angular momentum density can be written as[26]
 |
 |
Figure
We investigate the propagation properties of CAiV beams with x-polarization in uniaxial crystals. It is clear that the focused position can be controlled by changing the ratio of ne and no. In addition, the results show that the continuity and the self-acceleration effect of the CAiV beams become weaker as the proportion increases. From the intensity and the phase distributions of the CAiV beams, we find that the variation of the chirp parameters can affect the attenuation velocity of the vortex and control the intensity distribution. What is more, by changing the sign of the chirp parameter, we can control the intensity distribution of the CAiV beams. Lastly, we discuss the energy flow and the angular momentum of the CAiV beams through uniaxial crystals with different chirp parameters and discover that, when the distribution factor or the chirp parameter is increasing, the asymmetry of the angular momentum is more probable.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] |