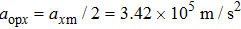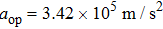† Corresponding author. E-mail:
Cold molecules have great scientific significance in high-resolution spectroscopy, precision measurement of physical constants, cold collision, and cold chemistry. Supersonic expansion is a conventional and versatile method to produce cold molecules with high kinetic energies. We theoretically show here that fast-moving molecules from supersonic expansion can be effectively decelerated to any desired velocity with a rotating laser beam. The orbiting focus spot of the red-detuned laser serves as a two-dimensional potential well for the molecules. We analyze the dynamics of the molecules inside the decelerating potential well and investigate the dependence of their phase acceptance by the potential well on the tilting angle of the laser beam. ND3 molecules are used in the test of the scheme and their trajectories under the impact of the decelerating potential well are numerically simulated using the Monte Carlo method. For instance, with a laser beam of 20 kW in power focused into a pot of 
Scientific interest in cold molecules has been strong for decades due to their important applications in a wide range of research areas, like high-resolution Doppler-free spectroscopy for optical frequency standards[1] or molecular clocks,[2] precision measurement of physical constants,[3] cold collision,[4] and cold chemistry.[5] By using their interaction with external fields, like electrical,[6–14] magnetic,[15–20] or even electromagnetic ones,[21–27] cold molecules from supersonic expansion, moving with high kinetic energy but in well-defined direction, can be effectively decelerated. So far, precise velocity control of the decelerated molecules has been experimentally demonstrated with either the electrostatic Stark decelerator or the Zeeman decelerator. However, the same level of velocity control on the molecule has not been realized with the optical Stark decelerator in experiment yet.
The optical Stark decelerator, capable of decelerating both polar and nonpolar molecules, was first demonstrated in experiment by Fulton et al. using a single laser pulse of ∼15 ns in duration[24] and later using pulsed optical lattices of 5.8 ns in duration.[25] Although the kinetic energy of the molecules was reported to have been reduced by up to 50% with intense laser fields on the order of 1011–1012 W/cm2, precision control on the final velocity of the decelerated molecules had not been achieved. Besides, the short duration and lack of mobility of the optical potential prevented it from being fully used in decelerating the molecules, though the well depth was as high as tens of or even hundreds of Kelvin in the above experiments. An alternative way is to work with optical potential wells of moderate laser intensities but with much longer durations. Surely, the optical potential well has to travel along with the decelerating molecules so that the deceleration process can be maintained. Friedrich first proposed scooping molecules from supersonic expansion at right angles by a non-resonant focused laser beam decelerating on a circular path.[21] However, due to lack of centripetal force in the radial direction, fast-moving molecules cannot follow the circular motion of the optical potential well, i.e., the laser focus spot. Recently, we proposed an optical Stark decelerator for molecules with a collinearly travelling potential well and analyzed the behavior of the trapped molecules inside.[28] To ensure the colinearity of the travelling potential well with the molecular beam, two laser reflective mirrors needed to spin simultaneously. It might not be easy to synchronize the motion of two spinning mirrors in a real experiment. Should the moving direction of the potential well be exactly collinear with that of the molecular beam? What would the deceleration effect be if there is a finite angle between the moving direction of the potential well and the molecular beam?
To answer the above questions, in this paper we study in detail the optical deceleration of molecules from supersonic expansion by an orbiting potential well, which is formed by rotating a red-detuned focusing laser beam via a single spinning mirror. The schematic diagram and deceleration principle of the scheme are first introduced, including the equation governing the motion of molecules confined in the potential well. Then, trajectories of ND3 molecules under the impact of the decelerating potential well are numerically simulated using the Monte Carlo method and the corresponding results are presented, which is followed by some discussion. A short conclusion is given in the end.
Figure
The red-detuned light field in the laser spot is assumed to have a Gaussian intensity distribution in the radial direction. The dipole potential energy for a molecule at position r (corresponding to the distance from the laser beam axis) can be given as


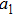


When the spinning mirror is under brake at an angular deceleration rate γ, the optical potential well will be slowed at a linear deceleration rate of 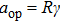
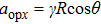
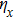
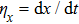

When the projection of the chosen linear deceleration rate of the optical potential well on the x direction is smaller than the maximal dipole force per unit mass available, i.e., 
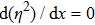
Let us take the ND3 molecule (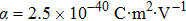


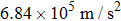
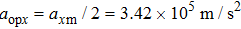

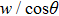




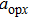
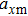


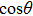

The motion of molecules in the y (or Y) direction is governed by the equation






 | Fig. 3. (color online) The force per unit mass experienced by the ND3 molecule as a function of displacement from the focus center along (a) the y axis and (b) the laser beam axis. |
The motion of molecules in the z direction is, however, more complicated. When the orbiting optical potential well is under deceleration of 
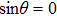
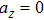
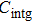

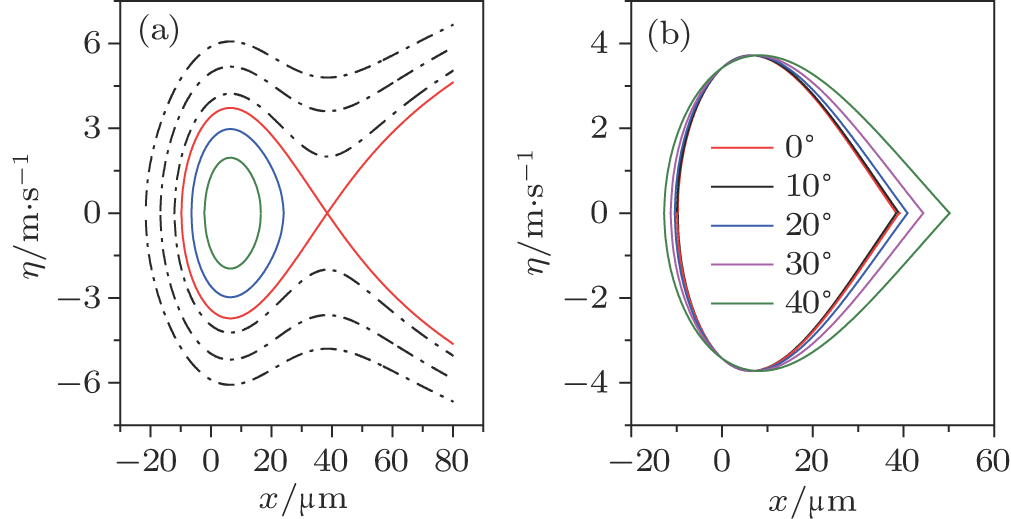
 | Fig. 4. (color online) The transverse phase acceptance of ND3 molecules in the z direction for cases of (a) θ = −1°, −5°, −10° and (b) θ = +1°, +5°, +10°. |
In fact, due to the coupling of the molecular motion in the three directions of x, y and z, the behavior of the molecule under the impact of the optical potential well is more complicated than in the above analysis. A three-dimensional (3D) numeric simulation of the trajectories of the molecules is necessary and can help us better understand their behavior.
To test the performance of the proposed scheme, the trajectories of ND3 molecules under the impact of the decelerating potential well are simulated using the Monte Carlo method. The pulsed ND3 molecular beam from supersonic expansion is assumed to have a Gaussian velocity distribution centered at 



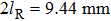
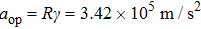


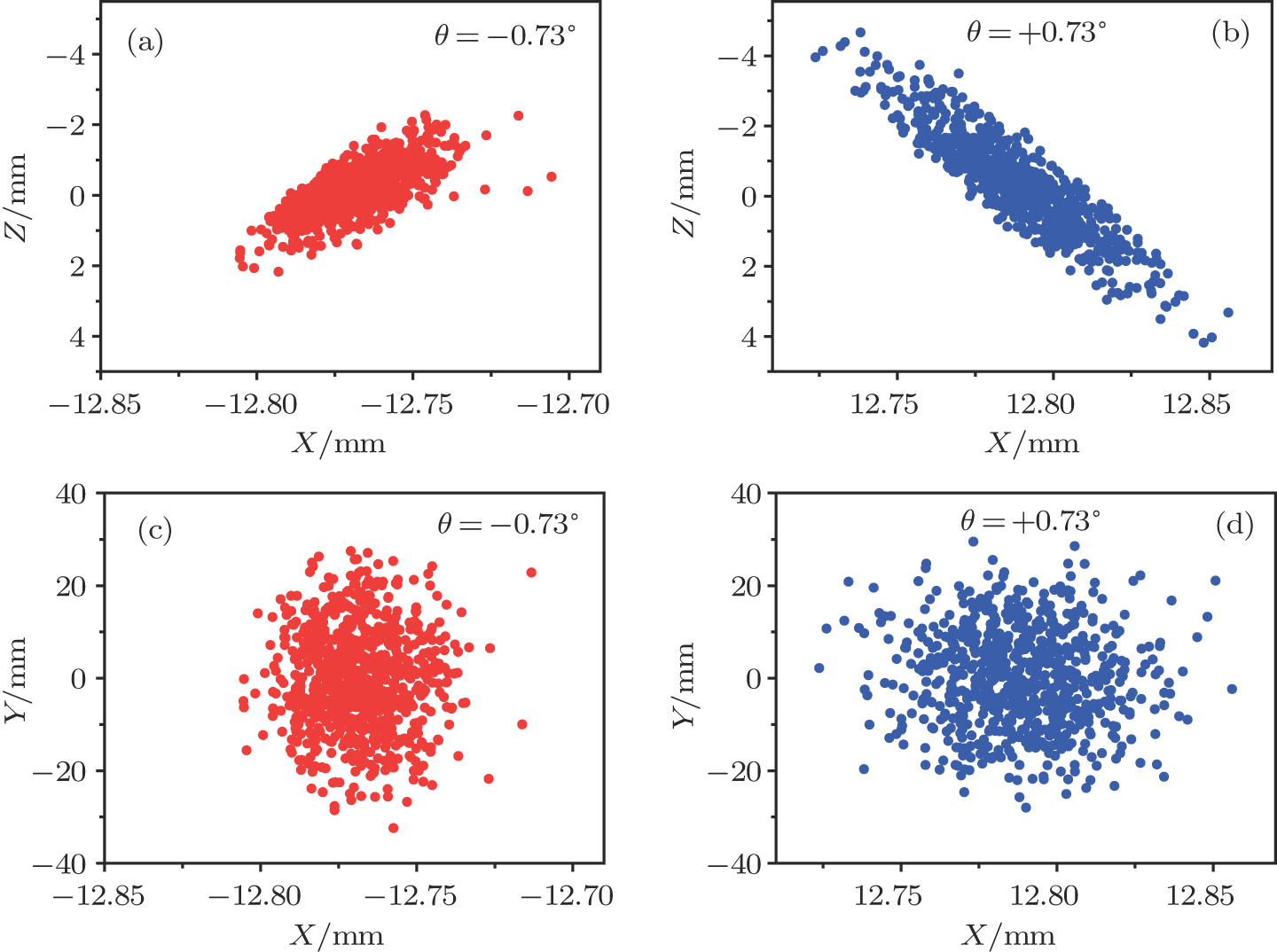 | Fig. 5. (color online) The spatial distributions of the decelerated molecular packet in the planes of XZ and XY for cases of (a), (c) θ =−0.73° and (b), (d) θ =+0.73°. |
Figure 

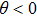
With current motor technology, the control of a spinning mirror with an angular deceleration rate γ on the order of 

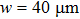


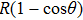
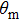
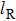
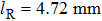
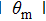
The total number N of molecules accepted by the potential trap can be estimated as N = fnV. Here, n is the number density of molecules. V is the effective volume of the trap, out of which the laser intensity decreases to below half the maximum value, estimated as 
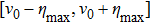

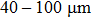


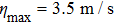
Once the polar molecules are decelerated to low-enough velocities, they can be either trapped locally by an electrostatic trap[30,31] or confined in an electrostatic storage ring.[32] In particular, an opto-electrostatic storage ring for cold dipolar molecules can be conveniently formed by incorporating the scheme into an electrostatic quadrupole or hexapole torus. Figure
In conclusion, we have theoretically studied the dynamics of decelerating a molecular beam from supersonic expansion with an orbiting optical potential well formed by rotating a red-detuned focusing laser beam via a spinning mirror. The dependence of the phase acceptance of the optical potential well for molecules on the tilting angle θ of the laser beam is thoroughly investigated. The trajectories of ND3 molecules under the impact of the decelerating potential well are numerically simulated using the Monte Carlo method. For instance, with the parameters of the laser power P = 20 kW, the waist radius of the laser focus spot 

| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] |