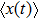† Corresponding author. E-mail:
Stochastic resonance (SR) is studied in an under-damped bistable system driven by the harmonic mixing signal and Gaussian white noise. Using the linear response theory (LRT), the expressions of the spectral amplification at fundamental and higher-order harmonic are obtained. The effects of damping coefficient, noise intensity, signal amplitude, and frequency on spectral amplifications are explored. Meanwhile, the power spectral density (PSD) and signal-to-noise ratio (SNR) are calculated to quantify SR and verify the theoretical results. The SNRs at the first and second harmonics exhibit a minimum first and a maximum later with increasing noise intensity. That is, both of the noise-induced suppression and resonance can be observed by choosing proper system parameters. Especially, when the ratio of the second harmonic amplitude to the fundamental one takes a large value, the SNR at the fundamental harmonic is a monotonic function of noise intensity and the SR phenomenon disappears.
Stochastic resonance (SR) can be considered as a synchronization of noise-induced hopping between the potential wells with a weak periodic forcing.[1–7] For a given nonlinear system, the time-scale matching condition for SR depends on the noise intensity and the period of the driving force. Therefore, noise, nonlinear potential, and periodic driving force have an important effect on the occurrence of SR. For example, Ai and Liu[7] found that an optimal stochastic potential may induce a doubly stochastic resonance (DSR). When the intensity of the stochastic potential is too large, the effect of the double well diminishes and the SR phenomenon disappears. However, most of studies on SR only involve the stochastic systems subjected to one periodic force. Recently, it is found that the harmonic mixing signal plays a constructive role in the context of vibrational resonance or controlling SR.[8–20] Landa and McClintock[8] found the vibrational resonance in an over-damped bistable system subjected to two periodic fields. Gitterman[9] showed that an additional periodic field has control over the shift of the resonance frequency, which is desirable in electronic devices or lasers. Chizhevsky[11,12] reported the experimental evidence of suppression of vibrational higher-order harmonics in a bistable vertical-cavity surface-emitting laser driven by two harmonic signals with very different frequencies. Yang et al.[14] investigated the response to the low-frequency of a bistable system perturbed by a low-frequency and a high-frequency excitation. Gammaitoni et al.[15,16] proposed the concept of controlling SR by using the periodic mixing signal and developed a general theoretical framework based on a rate equation approach. Schmid et al.[17] used the harmonic mixing signal to enhance or suppress the nonlinear SR in an over-damped bistable system. Grigorenko et al.[18] investigated the response of a bistable system with a frequency mixing force and reported the SR through the experiment of an iron garnet thin film. Jin et al.[19] studied the phenomenon of SR in an asymmetric bistable system subjected to the multiplicative and additive white noises and two periodic fields. Machura et al.[20] explored transport properties of the Brownian particles in a symmetric potential driven by the time-periodic biharmonic signals. They demonstrated that the symmetric driving cannot distinguish the direction in the frictionless case. In the case of over-damped motion, the antisymmetric driving leads to zero current. Hence, the study of the SR in nonlinear systems driven by two periodic fields and noise is of great signification.
Generally, most of the dynamical systems using in the study of SR are restricted to over-damped regimes, then the inertial term can be neglected and the theoretical analysis is simplified. However, for intermediate and small damping, the inertial effects should be considered and the under-damped dynamical systems are modeled. The SR phenomenon in the under-damped nonlinear systems and the effects of damping on dynamical behaviors have attracted attention from the scientists of different research fields.[21–31] Du et al.[21] and Wu et al.[22] found the damping induced stochastic multi-resonance in an under-damped bistable system with delay and without delay, respectively. Saikia[23] showed that the average input energy displays a peaking behavior with the damping coefficient. That is, damping plays a crucial role in the nature of SR in the multistable system. Lindner et al.[25] investigated the non-equilibrium dynamics of massive damped Brownian particles in an asymmetric periodic potential driven by colored noise. They demonstrated that the finite inertia can enhance the noise-induced transport in a ratchet potential and that for this transport there exhibits an optimal temperature of the embedding bath. Kang et al.[26,27] explored the SR phenomenon in an under-damped Duffing oscillator by using the moment method under the weak noise limit. Jin et al.[29,30] studied the noise-induced resonances in an under-damped periodic potential driven by colored noise and correlated noise, respectively. Xu et al.[31] implemented a numerical investigation of SR in the under-damped bistable system subjected to a weak asymmetric dichotomous noise and a periodic signal. Therefore, an under-damped bistable system is adopted to demonstrate the effects of the harmonic mixing signal on SR in this paper.
The objective of this investigation is to analyze SR phenomenon at fundamental and higher-order harmonic in an under-damped bistable system driven by harmonic mixing signal and Gaussian white noise. Using the LRT, the analytic expressions of the spectral amplification are derived at the fundamental and higher-order harmonic. The effects of the system parameters on the spectral amplification are discussed in Section
The model of concern is an under-damped particle moving in a bistable potential system, which is driven by Gaussian white noise and a harmonic mixing signal
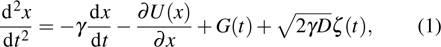 |


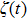
 |
The harmonic mixing signal G(t) is given by
 |
Let 
 |
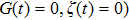

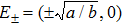

The corresponding Fokker–Planck equation of Eq. (
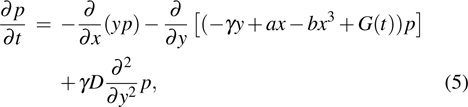 |
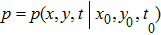
According to Eq. (
 |

From Eq. (
 |
 |
Using the two-state theory of SR, 
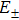

 |
Based on the definition of time-dependent mean value 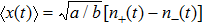

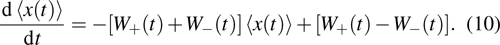 |
For the weak signal limit, the expansion of Eq. (
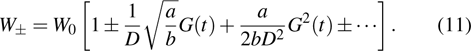 |
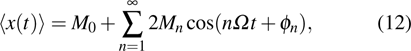 |

Then, the spectral amplification 
 |
 |
 |
 |
To understand the above theoretical results (
 | Fig. 1. (color online) Spectral amplification ηi (i = 1,2,3) versus noise intensity D for ε = 1, Ω = 0.1, and different γ. |
 | Fig. 2. (color online) Spectral amplification 
|
 | Fig. 3. (color online) Spectral amplification 
|
of the spectral amplification 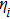


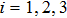

In Fig. 



In Fig. 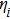


To better understand the influences of harmonic mixing signal on SR and verify the above theoretical results, the numerical results of Eq. (
Figure
 | Fig. 4. (color online) Time history and phase trajectory of the system (1) for a = b = 1, γ = 0.9, A = 0.01, Ω = 0.1, ε = 1. (a) D = 0.02; (b) D = 0.08; (c) D = 0.12; (c) D = 0.3. |
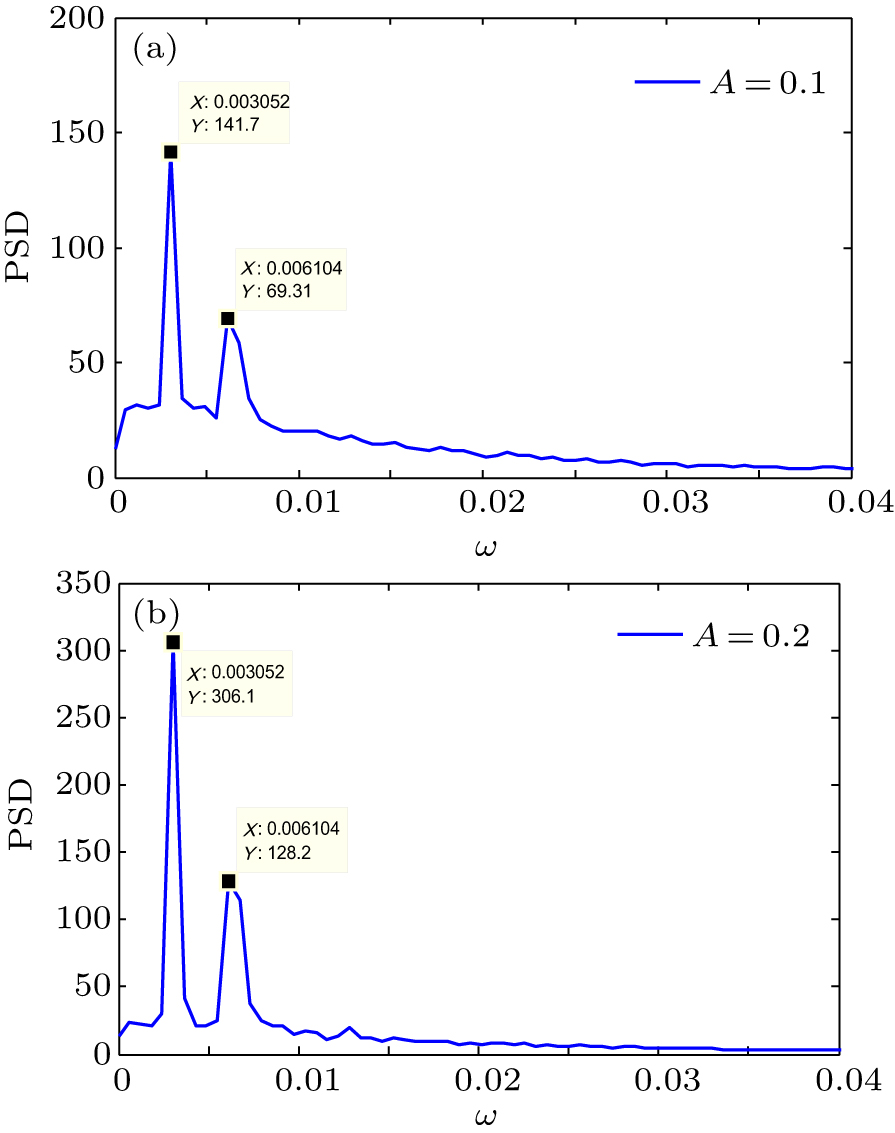
The PSD of the mean value 


In the following analysis, the signal-to-noise ratio (SNR) is introduced as a characteristic measure of SR. The SNR is calculated by 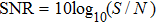
 | Fig. 7. (color online) The SNR1 and SNR2 of the system (1) as a function of noise intensity for a = b = 1, γ = 0.9, ε = 1, Ω = 0.1 with different A. |
 | Fig. 8. (color online) The SNR1 and SNR2 of system (1) as a function of noise intensity for a = b = 1, γ = 0.9, ε = 1, A = 0.01 with different Ω. |
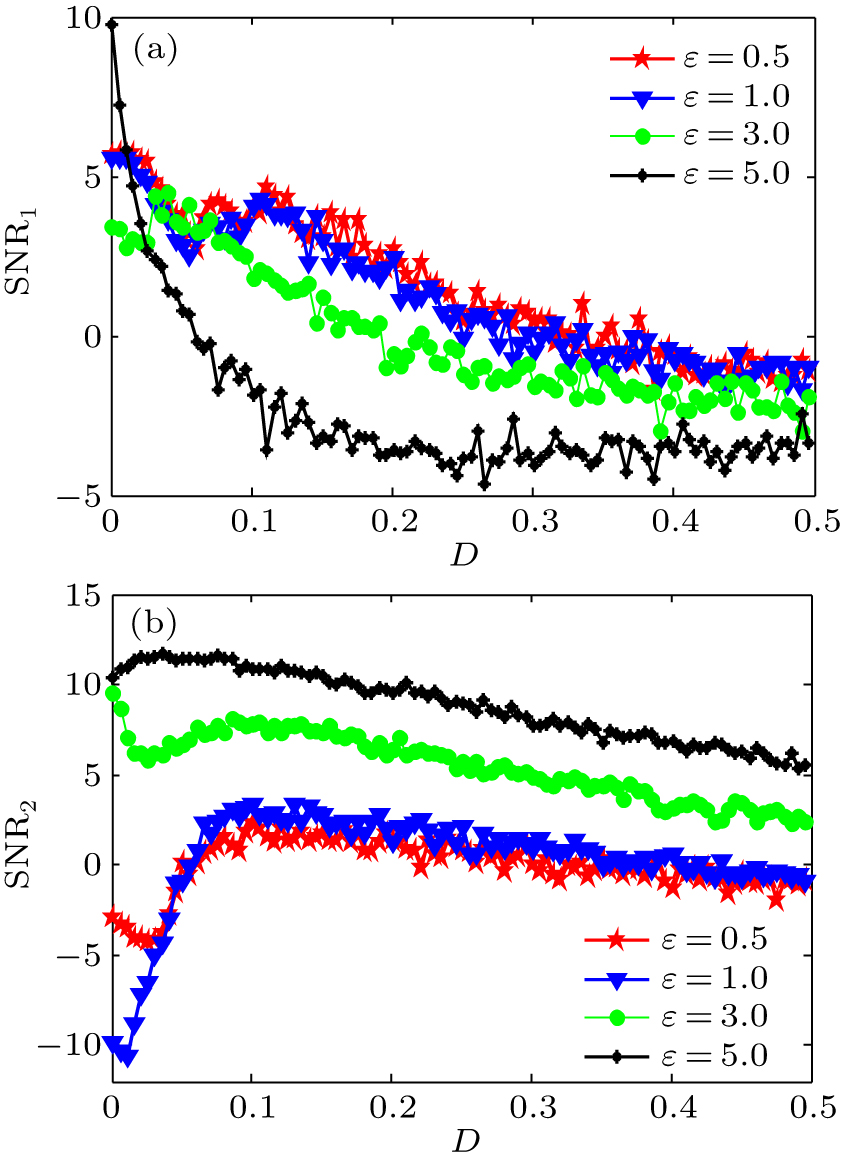 | Fig. 9. (color online) The SNR1 and SNR2 of the system (1) as a function of noise intensity for a = b = 1, γ = 0.9, Ω = 0.1, A = 0.1 with different ε. |
The effects of Ω on the SNR are shown in Fig.
In Fig. 

The phenomenon of SR is analyzed in an under-damped bistable system driven by harmonic mixing signal and Gaussian white noise. The expressions of spectral amplification at fundamental and higher-order harmonic are obtained by using the LRT. It is observed that the curves of the spectral amplification at first and second harmonic show the pronounced single-peak as noise intensity increases. The spectral amplification at third harmonic has a bimodal structure with the increase of noise intensity. That is, the noise-induced suppression and resonance can be found at the third harmonic. This bimodal structure can change to a unimodal one by increasing damping and signal frequency or decreasing the ratio of the second harmonic amplitude to the fundamental one. Moreover, the values of the spectral amplification at third harmonic are very smaller compared with those at first and second harmonic. The PSD and SNRs at the fundamental and second harmonic are calculated numerically to quantify the SR phenomenon and verify the theoretical results. It is shown that the curves of SNR exhibit a minimum first and a maximum later as the noise intensity increases. That is, both of the noise-induced suppression and resonance are found in this system. The values of SNR increase with increasing amplitude and decreasing signal frequency. The SNR at the fundamental harmonic is a monotonic function of noise intensity by choosing a certain value of the ratio of the second harmonic amplitude to the fundamental one.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] |