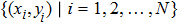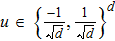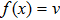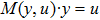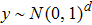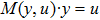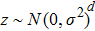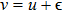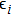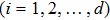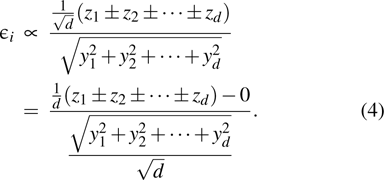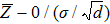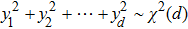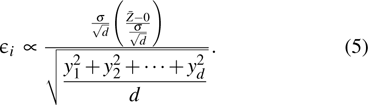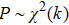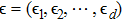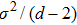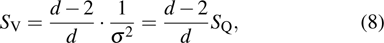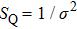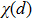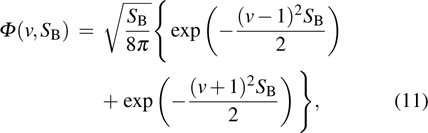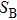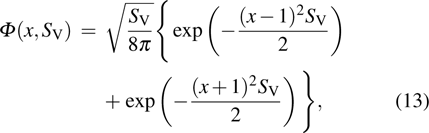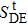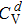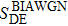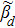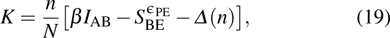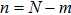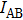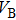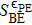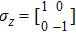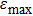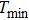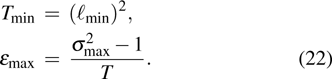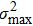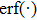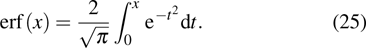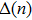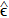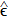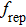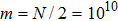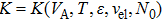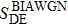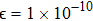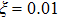Practical security of continuous-variable quantum key distribution under finite-dimensional effect of multi-dimensional reconciliation
1. IntroductionQuantum key distribution is a vital practical application in quantum information science.[1,2] It enables two legitimate parties, which are always called Alice and Bob, to produce a shared random secure secret key via a quantum channel, even in the existence of an eavesdropper, generally called Eve, who possesses limitless ability. Its security is guaranteed by the quantum mechanics laws, e.g., the Heisenberg uncertainty principle and the quantum no-cloning theorem. Currently two implementation methods, i.e., the discrete variable quantum key distribution and the continuous variable quantum key distribution (CVQKD), are often referenced. The CVQKD scheme usually encodes information on the position and momentum quadratures of quantum states.[3] It has the merits of a potentially high bit rate and compatibility with classical optical communication. In the past few years, the CVQKD have made a great number of achievements in both theories[3–5] and experiments.[6–8] One of the most notable achievements is that the Gaussian modulated coherent state (GMCS) scheme[6] has been proven to be secure against collective attacks[9–12] and coherent attacks.[13–16] Its practical securities with imperfection of the deployed devices in the CVQKD system have also been investigated.[17–24] In order to defend against practical attacks, real-time monitoring technologies are extensively adopted to prevent both attacks and signal disturbance.[25–28] Recently, field tests based on the GMCS scheme in telecommunication optical networks have been successfully implemented by several groups.[29–31]
A standard CVQKD system commonly consists of three phases, i.e., the quantum communication, the reconciliation, and the privacy amplification. In the quantum communication phase, Alice sends a string of X through a quantum channel. After performing a measurement of quadrature states by using a balanced homodyne detector, Bob obtains a string of Y which is correlated to X. Then, Alice and Bob obtain a string called the raw key. After that, with the purpose of checking the existence of Eve, the parameter estimation is indispensable and it determines whether they should abort or reserve the subset of remaining strings. In the reconciliation step, Alice and Bob achieve the same fix-length secret key strings by correcting errors between the secret key strings obtained by Alice and Bob. After the reconciliation step, Alice and Bob extract the secure secret key with a privacy amplification algorithm.
As is well-known, the reconciliation efficiency and speed are directly related to the transmission distance and the secret key rate of the involved CVQKD system. Generally, a high reconciliation efficiency improves the secure transmission distance and the secret key rate, while a high reconciliation speed is necessary to realize the high bit-rate CVQKD. Currently, the reconciliation has become a main bottleneck for the CVQKD implementation in the high-rate and long-distance scenarios. By far, several typical reconciliation schemes have been proposed. The proposed slice reconciliation scheme[32] quantifies the continuous variables to several layers, and then decodes them with correct-codes such as LDPC codes or BCH codes to obtain the same bit strings at both Alice and Bobʼs sides. This scheme has low decoding complexity, but its reconciliation efficiency is low and needs to be improved in a practical application. Because the raw keys follow a Gaussian distribution, it is more difficult to distinguish the signal in the presence of noise. In light of such a case, the post-selection scheme[33–37] was proposed to remove the small values and keep the big ones. Unfortunately, its security against arbitrary general attacks has not yet been proved. A most useful scheme called multi-dimensional reconciliation[38] was put forward to validly enhance the reconciliation efficiency and transmission distance in case of low signal-to-noise (SNR). With the assistance of multi-edge LDPC codes, such kinds of schemes[39,40] have achieved transmission distances up to 150 km[41] and decoding speeds up to 25 Mb/s.[42]
We note that all of the available multi-dimensional reconciliation schemes are essentially finite dimensions,[40] which actually deviates from the theoretical requirements of the reconciliation procedure. This deviation results in the so-called finite-dimensional effect (FDE), i.e., giving rise to the SNR mismatch between the quantum channel and the introduced virtual channel, subsequently, inducing the practical security loopholes. In this paper, we investigate the FDE of the multi-dimensional reconciliation scheme and its influences on the practical security of the involved CVQKD system. Since the multi-dimensional reconciliation scheme has finite dimensions, we find that the virtual channel follows a studentʼs t-distribution but not a Gaussian distribution, even if not the binary input additive white Gaussian noise channel (BIAWGNC), which is an approximation of the Gaussian channel at low SNR situation. Particularly, we find that the FDE may lead to the SNR mismatch between the quantum channel and the virtual channel. Consequently, it results in overestimation on the secret key rate, and then introduces practical security issues.
This paper is organized as follows. In Section 2, the multi-dimensional reconciliation scheme is reviewed briefly, then the FDE of the multi-dimensional reconciliation is investigated in Section 3. The influence of the FDE on the CVQKD is explored in Section 4. In Section 5, we investigate the practical loopholes in the involved CVQKD system induced by the FDE. Finally, the conclusions are drawn in Section 6.
2. Review of multi-dimensional reconciliation schemeDifferent from the previously practical security issues due to imperfections of devices deployed in the CVQKD system, the practical security loopholes studied in this work are induced by imperfections of the employed algorithm but not the devices. In other words, in this paper we focus on the imperfections of the multi-dimensional reconciliation scheme. For clarity, we review briefly the multi-dimensional reconciliation scheme in this section.
Generally, in the GMCS scheme, Aliceʼs information is encoded with a bivariate Gaussian distribution in phase space, and then Alice sends the information to Bob via a quantum channel interfered by the eavesdropper and channel noise. After Bobʼs measurement with a balanced homodyne detector, Alice and Bob share N couples of correlated variables
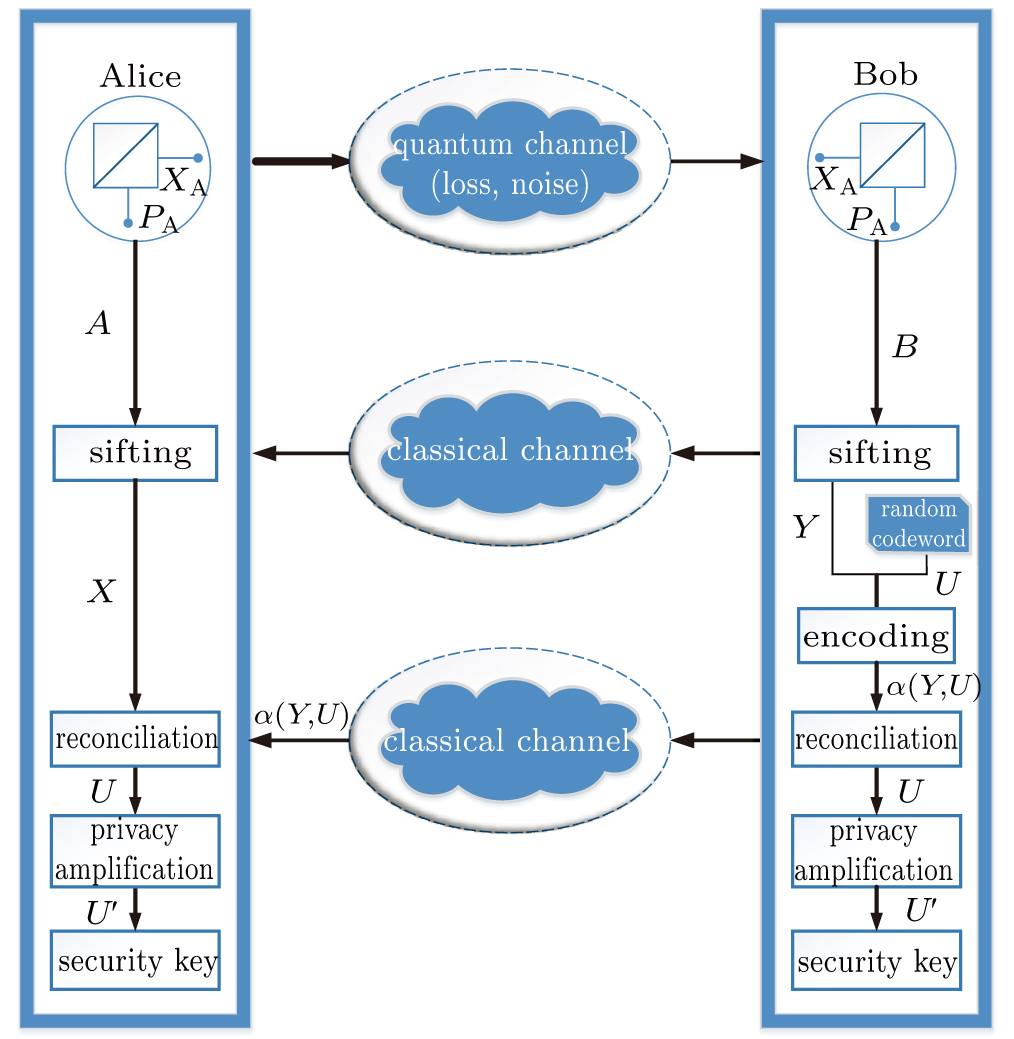
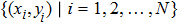, i.e., the raw key data, where xi is the quadrature modulated by Alice, and yi is the quadrature measured by Bob. Here N is the total number of transmitted data, N = m + n. Then, m couples of variables are randomly selected to estimate the quantities that are required to compute the secret key rate, and the remaining n pairs of variables are used for the key establishment. In the wake of these steps, the data are exchanged through a public authenticated channel so that one may execute the reconciliation procedure which distills an identical binary bit string between two parties. Thus the virtual channel which is used to exchange data is built. The schematic of the CVQKD with multi-dimensional reconciliation scheme is shown in Fig. 1.
The basic idea of the multi-dimensional reconciliation scheme is as follows. Firstly, map the non-uniform Gaussian-distributed variable space generated by the quantum communication into a uniform-distributed variable space. Then, randomly choose a stochastic code words space whose prior probability meets a uniform distribution. After that, the chosen code words are transmitted over a public authenticated classical channel. In such a case, the two legitimated parties who share the key will not leak any side information about the code words so that Eve cannot obtain any extra key information. The multi-dimensional reconciliation scheme executes the following steps.
Step 1 Alice and Bob have to divide the obtained continuous variables into consecutive d-dimensional vectors in the multi-dimensional reconciliation scheme for the purposes of security. A common tactic is straightforward to assemble every d successive continuous variables into a d-dimensional vector. One may also recombine those elements after rearranging the continuous sequences such that
,
, and
.
Step 2 Bob generates a uniform distribution random binary string S of length d (in the reverse reconciliation scheme) via a quantum random number generator. The total size
of the code S is bounded by the mutual information between Alice and Bob, i.e.,
. Then, Bob randomly chooses d-dimensional vector
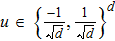according to the binary phase shift keying (BPSK) encoding, and sends the side information expressed by function f satisfying
and the generated syndrome to Alice. After that, Alice computes
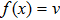with the function transmitted over a public authenticated classic channel.
Step 3 Alice receives the noisy version of u. In this way, the two parties, i.e., Alice and Bob, build a virtual channel with input u and output v. Afterwards, Alice tries to reconstruct u by utilizing the intensive sum-product belief propagation algorithm for decoding the LDPC code.[43,44] The virtual channel noise is eliminated and Alice shares the same key with Bob.
3. Finite-dimensional effect of multi-dimensional reconciliationAccording to the multi-dimensional reconciliation scheme described in the above section, the function f rotates the quadrature measure y into binary codeword u. In practice, one may choose a function M so that
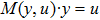for every word
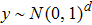sent by Bob and every codeword
in the regime of reverse reconciliation. Then, Bob sends
to Alice through a public authenticated channel (the multiplication and division operators are defined in
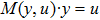and
).[40] Assume the quantum communication procedure to be a standard linear model, the following relationship can be obtained:[11]
with
and
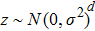, where
, and η, T, z are the detection efficiency, the transmission efficiency, and the quantum channel noise term, respectively. In order to derive the virtual channel model with input u and output v more explicitly, we set
, i.e., without considering channel loss in the reverse reconciliation. Then, the noisy version of u is deduced as follows:
The multi-dimensional noise in the virtual channel is given by the term
, such that
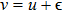
which is the rotated version of quantum channel noise. Due to the spherical symmetry and independence of the distribution on
z and
x, the noise of the virtual channel follows the distribution
Hereto we have established a virtual channel and succeeded in reducing the reconciliation problem to a channel coding problem. In this way, one can graft the post-processing procedure of CVQKD on searching for a good code which has been developed maturely in the traditional communication system.
The noise of the virtual channel with input u and output v is given by
According to the multi-dimensional reconciliation scheme, the continuous variable
x and quantum noise
z are decomposed into
d-dimensional vectors, and
u satisfies
. So the noise
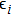
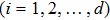
, which is the element of vector
, can be rewritten as
Let
. Clearly,
has zero mean and
variance. Subsequently,
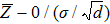
follows a normal distribution and
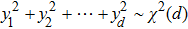
. Then, equation (
4) may be expressed in a simplified form
In the probability theory,
[45] the studentʼs
t-distribution is defined as follows. Let
Q be a standard normal distribution, i.e.,
, and
P be a chi-squared distribution, i.e.,
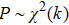
. Meanwhile,
Q and
P are independent. Then let
The
t satisfies the studentʼs
t-distribution with
k degrees of freedom. In terms of the above definition of the studentʼs
t-distribution, the distribution of noise over the virtual channel
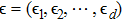
can be expressed as follows:
That is, the noise of the virtual channel follows the studentʼs
t-distribution with
d degrees of freedom. The noise
has a zero mean and a noise variance of
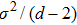
. Clearly, such a channel does not follow the Gaussian distribution.
Now we study the SNR of the virtual channel. According to the above calculation, the SNR of the virtual channel may be calculated by
where
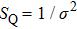
is the SNR of the quantum channel (physical channel).
Apparently, the SNR of the virtual channel is associated with the reconciliation dimension d. The FDE of the multi-dimensional reconciliation will be eliminated when
. Actually, since the norm of d-dimensional vector x follows the
distribution, when d approaches to infinity,
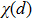is approximately close to the Dirac distribution. In this way, the small absolute value coordinates benefit the final key extraction and become abundant. In addition, with the dimension d becoming larger, the virtual channel becomes closer to the BIAWGN channel, even the AWGN channel in the practical CVQKD system.
4. Influences of finite-dimensional effect on CVQKD systemIn this section, we investigate the impacts of the FDE on the channel capacity, reconciliation efficiency, secure secret key rate, and secure transmission distance of the CVQKD system.
First, we consider the impacts of the FDE on the channel capacity. The capacity of the Gaussian channel, i.e., the AWGN channel, is given by
where
refers to the SNR which is equal to
. However, this channel capacity cannot be reached since the multi-dimensional reconciliation scheme employs the BPSK encoding. Previously, the virtual channel is often regarded approximately as a BIAWGN channel, which uses a random variable
as its input and outputs a random variable
, where
is a zero mean Gaussian random variable with variance
. The capacity of BIAWGN is
where
and
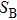
corresponds to the SNR of the BIAWGN channel.
Since the practical virtual channel actually follows the studentʼs t-distribution, the capacity of the virtual channel is given by
where
refers to the SNR of the virtual channel which is equal to
, and
Here
and
are the Beta function and Digamma function, respectively. The Beta function is given by
and the Digamma function is expressed as
In the multi-dimensional reconciliation scheme, the dimension is only restricted to d = 1,2,4,8 according to the Hurwitz theorem of composition algebras,[38] or the dimension is restricted to d = 16.[40] Figure 2 demonstrates the influences of the FDE on the channel capacity when d = 8. As a comparison, we also plot the AWGN channel capacity and the BIAWGN channel capacity. As one may see from Fig. 2, the channel capacities of the Gaussian channel and BIAWGN channel are approximately equal in the low SNR situation. However when d = 8, the 8-dimensional channel capacity is much lower than that of the BIAWGN channel. Obviously, this deviation will influence inevitably the performance and practical security of the involved CVQKD system.
Now we investigate the impacts of the FDE on the reconciliation efficiency. Generally, the reconciliation efficiency β is defined as
where
R is the code rate used for the reconciliation procedure, and
is the channel capacity when
S corresponds to the SNR. Consider the impacts of the FDE, based on Eqs. (
10), (
12), and (
17), the reconciliation efficiency
in the virtual channel is given by
where
β in Eq. (
18) represents the reconciliation efficiency of the CVQKD system over the BIAWGN channel. The
which enters to the
is the SNR threshold on the BIWAGN channel for the LDPC codes (size 2
20) predicted by the density evolution. The
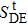
which enters to the
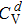
is the threshold on the studentʼs
t-distribution channel for the LDPC codes (size 2
20) predicted by the density evolution. Based on the density evolution,
[43]
is smaller than
which enters the
. There is no definite numerical relationship between
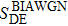
and
. Clearly, the SNR between the quantum channel and virtual channel would match when
d trends to infinity. Then the reconciliation efficiency
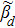
approximates
β in the AWGN channel.
In Table 1, we list the reconciliation efficiency
in the virtual channel based on Eqs. (12), (17), and (18), which corresponds to the 8-dimensional reconciliation. The code rate R is set as 0.02 and 0.05 quoted from Refs. [40] and [39]. Apparently, since the virtual channel is not exactly a BIAWGN channel, the efficiency is lower than the reconciliation efficiency predicted by the density evolution on the BIAWGN channel. It is shown that the reconciliation efficiency descends from 96.9% to 91.3% when the FDE is considered.
Finally, we consider the influence of the FDE on the secret key rate. According to Ref. [11], the secret key rate K with n received pulses used for key establishment can be represented as follows:
where
,
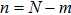
is the efficiency of the reverse reconciliation,
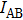
represents the mutual information
[46] between Alice and Bob, which can be derived from Bobʼs measured variance
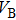
and the conditional variance
, i.e.,
and
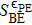
represents the maximal value of the Holevo information compatible with statistics except with probability
. Since Bobʼs detector is calibrated before the experiment and cannot be controlled by Eve,
is determined by the following covariance matrix between Alice and Bob with finite-size effect:
where matrices
and
,
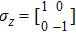
and
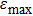
correspond to the lower bound of the transmission efficiency
T and the upper bound of the excess noise
ε, respectively. When
m is large enough (e.g.,
), we could compute
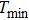
and
as follows:
[11]
Furthermore, when
m is large enough,
and
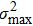
can be calculated by
where
follows
and
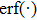
is the error function defined as
Meanwhile,
is calculated as follows:
where
, and
are symplectic eigenvalues derived from the covariance matrices
with
In Eq. (19),
is a linear function of n and related to the security of privacy amplification. For a CVQKD system,
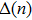can be expressed as[11]
where parameters
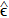
and
, which are virtual parameters and can be optimized in computation, denote the smoothing parameter and the failure probability of the privacy amplification, respectively. In calculation,
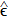
and
are usually set to be equal to
, i.e.,
, because it is observed that the value of
mainly depends on
n instead of these two parameters.
Based on Eqs. (27) and (28), one may evaluate the secret key bit rate with finite-size effects under collective attacks. For a practical pulsed CVQKD system, the bit rate of the secret key is given by
where the secret key rate
K is defined in Eq. (
19) and
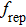
represents the repetition frequency. Let
m be the typical value
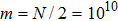
, the secret key rate may be regarded as a function
.
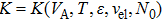
Figure 3 demonstrates the relationship between the secret key rate and the transmission distance with various reconciliation efficiencies. It shows that the change of the reconciliation efficiencies dramatically decreases the secret key rate, while the secure transmission distance is approximately 20 km shorter than the original one when we have not accounted for the FDE. It is shown that the value with FDE is lower than that without FDE at transmitted distance d = 93 km. If the FDE is not considered, it would lead to the misevaluation of the secret key rate, and then introduce a potential safety risk. Thus we can see that the FDE is significant for a practical CVQKD system.
5. Practical security loopholesCommonly, the information characteristic of the introduced virtual channel should accord with that of the quantum channel in a CVQKD scheme. However, if they are not matching, for example, the SNRs between the quantum channel and the virtual channel are not the same, miscalculations on the secret key rate are generated. Consequently, such kinds of imperfections will inevitably degrade the practical security of the CVQKD system. The above section has demonstrated clearly the difference of SNRs between the quantum channel and the introduced virtual channel. Such difference, which is generated by the imperfections of the multi-dimensional reconciliation scheme, will lead to loopholes for the practical security. Actually, Figure 3 has shown that the CVQKD system is insecure beyond about 100 km.
In the above section, we have demonstrated the influences of the FDE on the secure secret key rate and secure transmission distance. The most significant factor is that the FDE leads to the SNR mismatch between the quantum channel and the virtual channel. For example, the noise variation of the virtual channel is 4/3 times of the one of the physical channel (Gaussian channel) when d = 8. Correspondingly, the SNR of the virtual channel is 3/4 times of that of the quantum channel. Such change will decrease the actual reconciliation efficiency, which has a significant influence on the secret key rate.
Figure 4 plotted, respectively, for different reconciliation efficiency β and modulation variation VA shows that the secure secret key rates will drastically decrease and the secure transmitted distances will become shorter when considering the FDE. In addition, the FDE would be greater as the modulation VA becomes larger. This explains that there is a gap between the secret key rate considering FDE and the one without considering FDE. In this way, Eve can utilize such a gap to engage in attack, such as intercept-resend attacks. Then Eve can gain access to some of the information on the legitimate parties. Thus the FDE can induce significant practical security issues.
6. ConclusionWe have investigated the imperfections of the multi-dimensional reconciliation scheme and the induced practical security loopholes. Such kinds of imperfections come from the algorithm but are not induced by the devices of the CVQKD system, which has been investigated previously. We find that the binary input virtual channel is different from the BIAWGN channel due to the FDE. In particular, the FDE leads to SNR mismatch between the quantum channel and the virtual channel, and subsequently results in significant influences on the channel capacity, the reconciliation efficiency, and the secure secret key rate. Consequently, it leads to overestimation on the secret key rate, and then introduces practical security loopholes.
