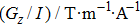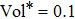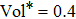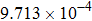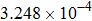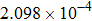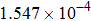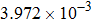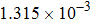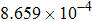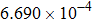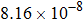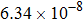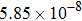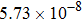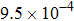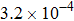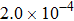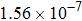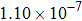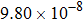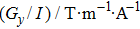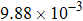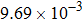† Corresponding author. E-mail:
A topology optimization method based on the solid isotropic material with penalization interpolation scheme is utilized for designing gradient coils for use in magnetic resonance microscopy. Unlike the popular stream function method, the proposed method has design variables that are the distribution of conductive material. A voltage-driven transverse gradient coil is proposed to be used as micro-scale magnetic resonance imaging (MRI) gradient coils, thus avoiding introducing a coil-winding pattern and simplifying the coil configuration. The proposed method avoids post-processing errors that occur when the continuous current density is approximated by discrete wires in the stream function approach. The feasibility and accuracy of the method are verified through designing the z-gradient and y-gradient coils on a cylindrical surface. Numerical design results show that the proposed method can provide a new coil layout in a compact design space.
Magnetic resonance imaging (MRI) is widely used in medical diagnosis, biological research, and material science. In recent years, it has been used on a microscale with spatial resolutions of less than 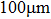

Recently, a great deal of research has been reported for rapid switching and high-resolution MR devices on a microscale for cell imaging. This research focuses on the miniaturization of core components of MRI equipment. Most of the studies are aimed at the downscaling of MR receiver coils, which can enhance the local SNR.[2,4–7] The gradient value of the gradient magnetic field is also a key factor restricting the quality of imaging. The miniaturization of the gradient coil reduces the distance between the coil and the sample, improves the efficiency of the coil, and increases its gradient value. In this paper, we will discuss gradient coils for microscale MRI applications. Whether there are simple and efficient micro coil configurations is an open question. In this paper, voltage-driven gradient coils are proposed, which are designed by a topology optimization method. The method offers a means to design custom coils with best performance.
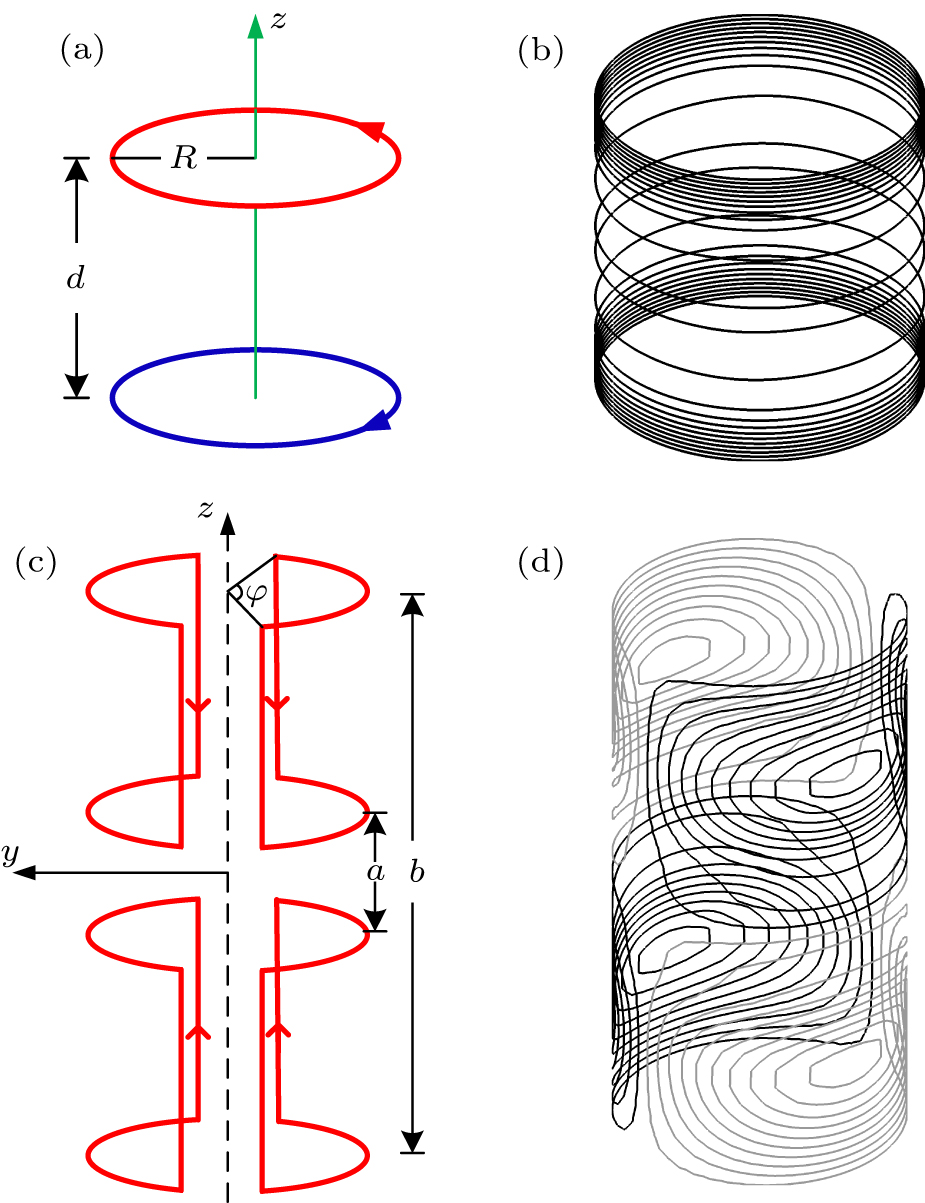
To date, much research has focused on improving the performance of gradient coils. The reported design methods can be divided into two types: discrete wire techniques and current density techniques.[8] Discrete wire techniques are based on the optimization of the geometry (size/position) of independent current loops to produce a required magnetic field. The most basic examples of the discrete wire techniques are the Maxwell coil (Fig. 
The current density techniques compute a continuous current distribution which needs to be approximated by discrete wires or current paths. A number of optimization methods have been developed in order to determine the current density distribution. These include the target field method[11–14] and the stream function method.[15–18] The target method developed by Turner[19] uses a Fourier–Bessel expansion of the magnetic field generated by current flowing on a cylindrical surface, and uses Fourier transforms to obtain an ideal current density solution. The stream function method is based on meshing the current carrying surface into an array of finite elements to approximate distributions of stream functions, where the current density vector design variables are transformed into scalar design variables. The numerical methods mainly include finite difference method,[20] finite element method (FEM),[21] and boundary element method.[16] These types of techniques have been extended by optimizing some features of coils, such as the inductance,[22,23] stored magnetic energy,[24–26] dissipated power,[27–29] torque,[30] coil width, and nonlinear gradient coils.[31] The current density techniques generally lead to more compact coils resulting in increased efficiency, as well as less concentrated current resulting in lower inductance.[32] Figures
Even though the current density technique is successful in designing the MR gradient coils, it also has some limitations. Firstly, the current distribution derived by these methods must be approximated by discrete wires or current paths. As for small numbers of wires, the approximation to the current distribution is poor, resulting in deviation of the calculated magnetic fields. Secondly, return paths must be introduced to assure that equal currents flow in all paths. The return currents in these wires produce a smaller negative field which reduces somewhat the gradient achievable, and lead to a longer geometry for the current-carrying surface and a higher inductance. Thirdly, the complexity of the configuration increases the difficulty in making gradient coils for microscale MRI.
Topology optimization can be defined as a method with material suitably placed within a prescribed design domain in order to minimize or maximize the given objective function subject to userʼs specified design constraints.[34] The method as a design process has spread to a wide range of applications in different fields of engineering over the years, such as mechanical structures,[35,36] heat conduction,[36] unsteady incompressible Navier–Stokes flows,[38] and multi-physics actuators.[39,40]
In this paper, a method based on the topology optimization of a material distribution is proposed to optimize the configuration of gradient coils, and a gradient-based optimization technique is utilized to solve the design problems. The coil configuration can be obtained, avoiding the usual system errors which may appear in a discrete approximation between the calculated continuous current density and the practical realization of discrete current paths. There is also no presetting limit to the shape of coil configurations.
In this section, the proposed topology optimization method (TOM) of designing the gradient coils is discussed in detail. The design process can be divided into two main steps. The first step is to establish the relationship between the surface current and the design variables via a description of the gradient coil, and then to derive the performance parameters of the electromagnetic coil, such as the magnetic field and energy consumption. The second step is to find the optimal coil configuration under a particular application by optimization procedure. Here, the design of gradient coils on a cylindrical surface serves as an example. In order to simplify the optimization model and reduce the amount of calculation, the developable property of a cylindrical surface and the layout symmetry of gradient coils are utilized. The proposed method can also be extended to other geometries or physical boundary conditions.
As shown in Fig. 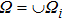
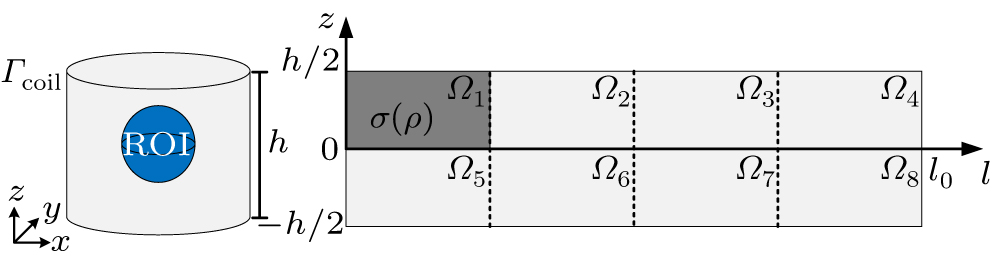 | Fig. 2. (color online) Current-carrying surface 
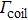
|
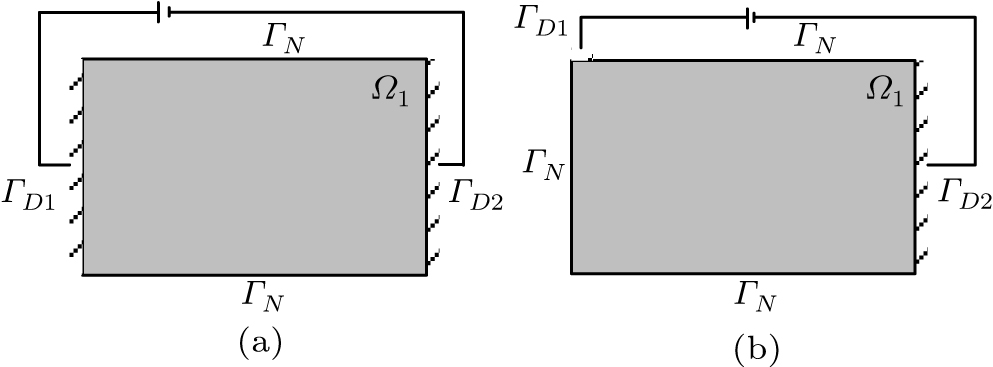
Before optimization, the method of driving the gradient coils and boundary condition specifications of the design domain must be determined. For the traditional stream function design method, the electric current drive mode is typically used and the electric current is calculated directly by using the gradient of the stream function. Then the analytical Biot–Savart equation is used to calculate the magnetic field under the given current distribution. For the proposed method, the design variables of the gradient coil are the conductor distribution of gradient coil on the design surface. Therefore, the electric problem has to be solved numerically (here the finite element method is used) under either voltage or current boundary condition. Compared with the current boundary conditions, the voltage boundary conditions can be straightforward implemented based on the standard finite element solution. In this paper, the proposed gradient coil is driven by applying a voltage at a predefined position. For different types of gradient coils, the input voltage can be specified by the designer as shown in Fig.
 | Fig. 3. Boundary conditions of design subdomain Ω1 for (a) z-gradient coils and (b) y-gradient coils. |
The z-gradient magnetic field can be produced by a circumferential current, so the input voltage for z-gradient coils can be applied to the left and right ends of the developed design surface. The corresponding boundary condition of subdomain Ω1 is shown in Fig. 
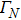
As shown in Figs. 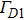
In this paper, the design variable ρ is not the current density or the stream function, but the spatial distribution of conductive material, which is reflected in the conductivity of the gradient coils. The distribution is described by the density field 
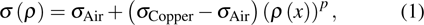 |
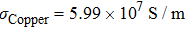
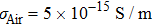
The electric problem is analyzed in the design domain Ω, together with boundary conditions on 
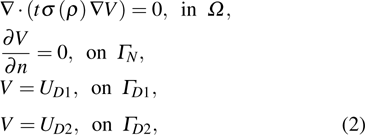 |

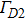


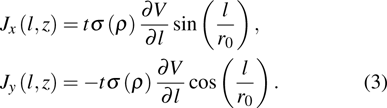 |
The z-component of the magnetic field 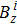
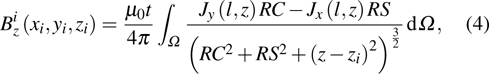 |

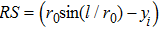
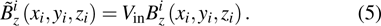 |
The goal of the optimization procedure is to find a conductive material distribution in the design domain Ω in order to minimize the objective function for magnetic field linearity, which is defined as the least-square form of the residual between the actual magnetic field and the desired magnetic field
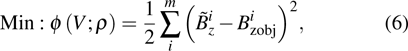 |

Through the analysis above, the relationship among the magnetic field strength, the current density, and the design variable is established. The formulation is based on the regular discretization of the design domain Ω that is covered by a given shape. Here, the continuous material distribution is approximated by C 0-continuous finite elements in the design domain. The density variable can be expressed as
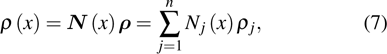 |


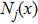
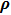

 |
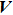


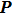
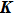
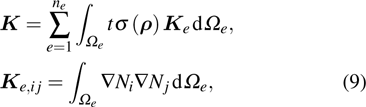 |
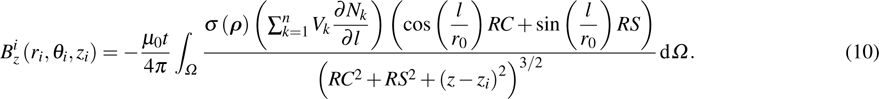 |
In order to obtain a binary configuration, it is common to choose an auxiliary objective function, such as the resistance, input voltage 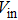
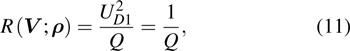 |

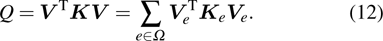 |
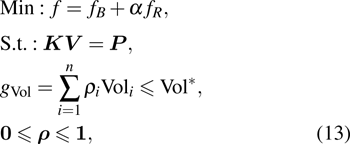 |
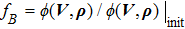
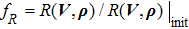





The optimization problem can be solved iteratively by using the gradient-based optimization schemes. In this paper, the gradients with respect to the design variable are obtained using adjoint analysis. The detailed sensitivity derivation is given in the appendix. In each iteration, the following computational steps are performed:
i) Solve the current continuity equation (
ii) Perform objective function and sensitivity analysis to obtain the derivatives of the objective and constraint function with respect to the design variable Eqs. (
iii) Update the design variable based on the optimality criterion (OC) method[43] or method of moving asymptotes (MMA).[44] In this paper, we will use a standard OC method, because there is only one design constraint about material volume fraction.
The procedure has converged when the changes of design variable δ for subsequent iterations are less than a threshold η (typically 103). We detail the optimization process in Fig.
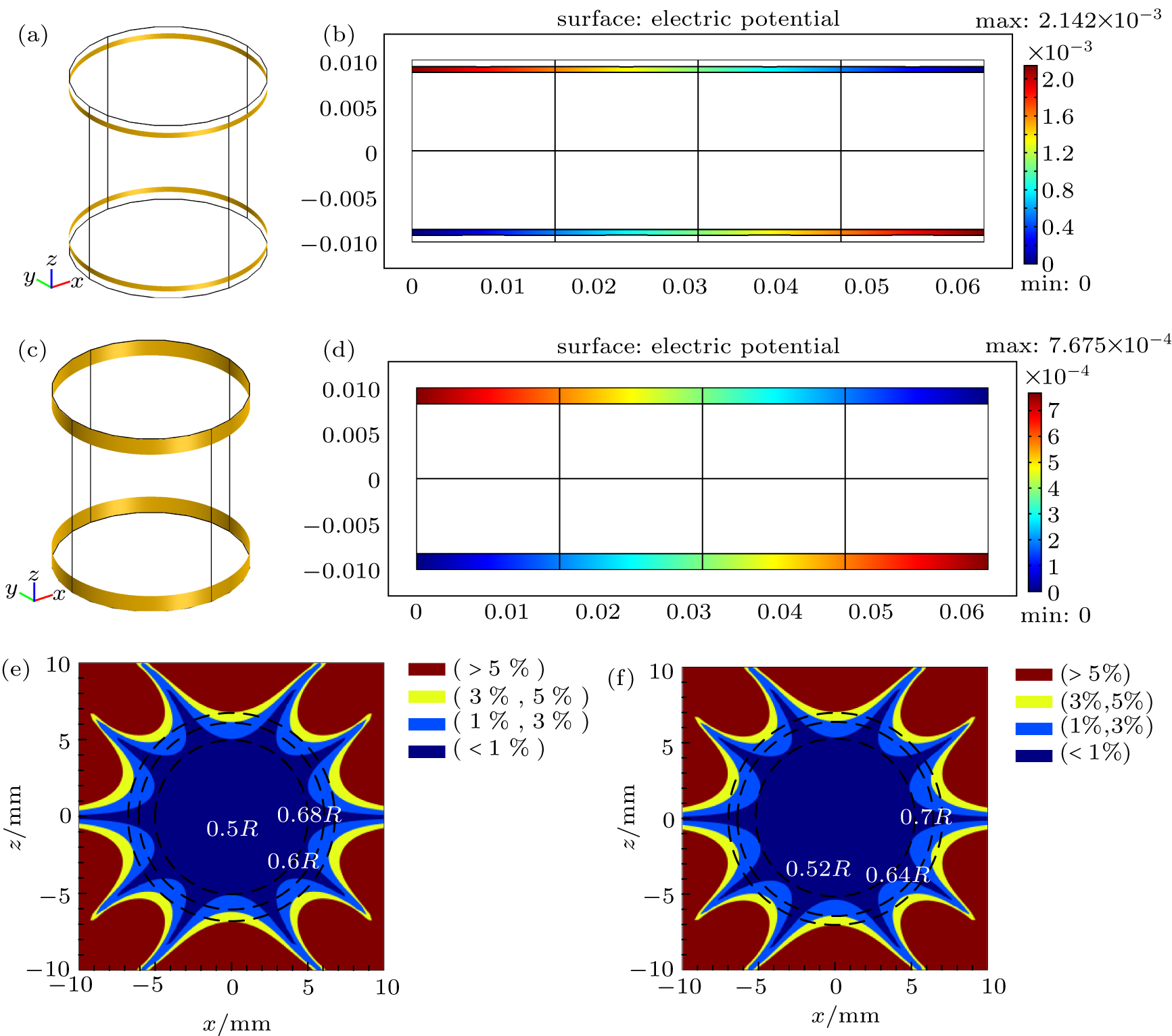
For the applications of microscale MRI, the gradient coil is designed on a cylindrical surface as shown in Fig. 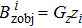
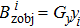
Here, the field inaccuracy is defined as the linear gradient deviation of magnetic field 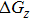
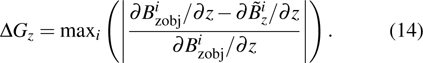 |
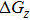

The most straightforward optimization model is the single objective model, where the weight coefficient α in Eq. (
 | Fig. 5. One-eighth final configurations of z-gradient coils using single objective optimization model with different parameters. |
| Table 1.
Input voltage and field inaccuracy of gradient coils listed in Fig. |
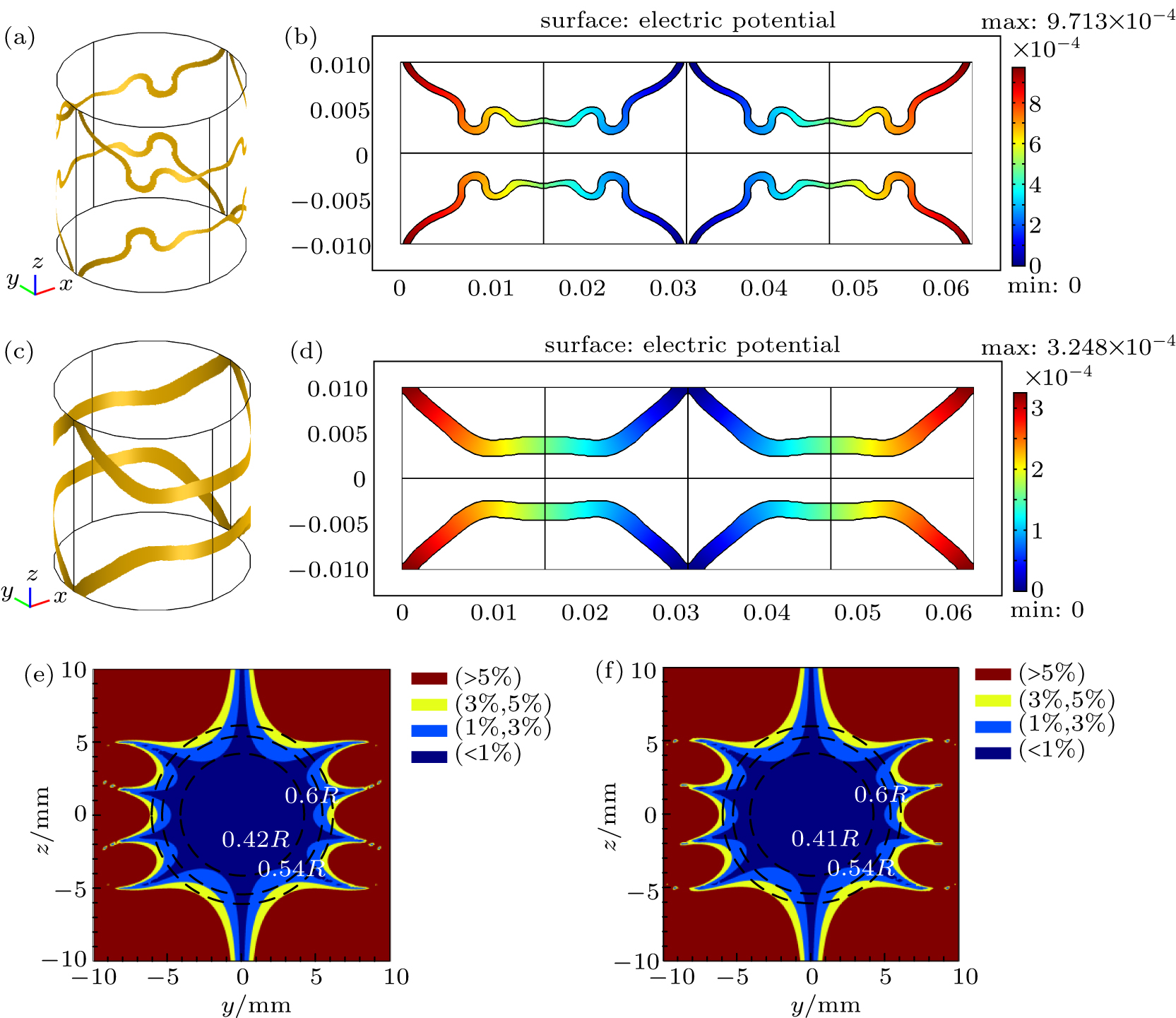
Figure 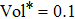
 | Fig. 6. One-eighth final configurations of y-gradient coils using single objective optimization model with 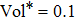
|
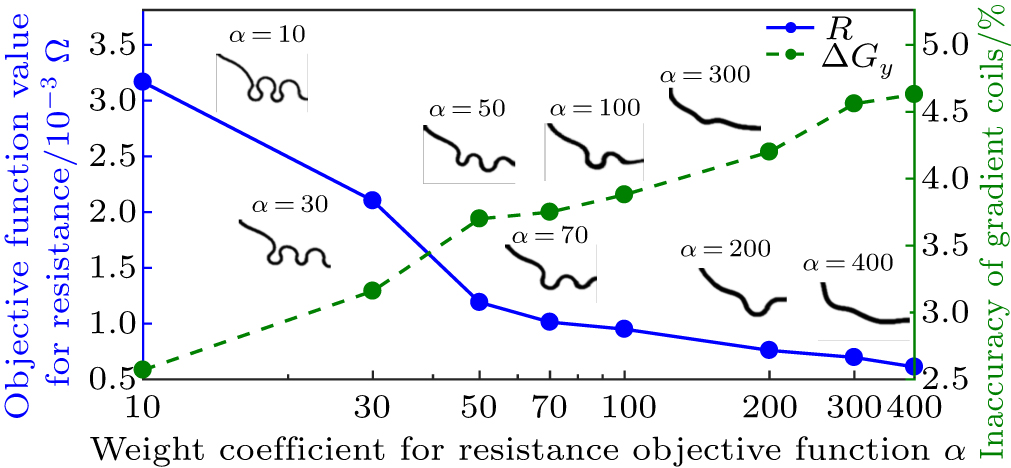
In physical terms, due to the lack of accurate constraints on input voltage for the desired magnetic field, design variables can hardly converge to the binary configuration. In other words, minimizing the input voltage (or its equivalent, such as resistance and dissipated power) is necessary for the optimal result to converge to a black-and-white pattern in the proposed optimization model. In this paper, in order to obtain a reasonable optimized result, the auxiliary objective function is introduced into the optimization model with non-zero weight coefficient α.
Figure
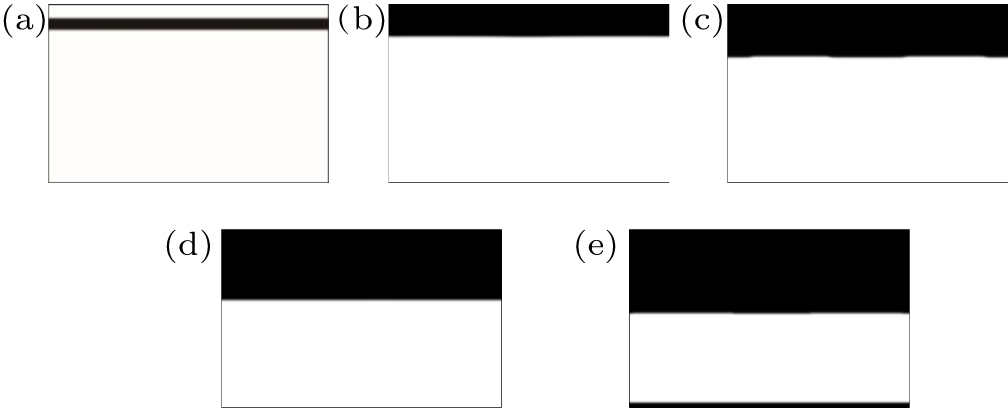 | Fig. 7. Final configurations of z-gradient coils with the volume fractions ranging from 0.1 to 0.5, Here, the weight coefficient α of resistance objective function is chosen as 100 and p = 5. |
| Table 2.
Performance parameters of z-gradient coils presented in Fig. |
From Table
By adjusting the weight coefficient α, a series of different coil configurations can be obtained. Figures 
Figure
 | Fig. 11. Coil configurations of y-gradient coils with volume fractions of (a) 0.1, (b) 0.2, (c) 0.3, and (d) 0.4. Here α =100 and p = 5. |
| Table 3.
Performance parameters of z-gradient coils presented in Fig. |
Compared with conventional y-gradient coils, the coil configurations are much simple, easy to make on a microscale, with very low inductance and resistance. The required current value is larger, because the magnetic field is produced by a single wire. However, due to the small resistance, the coil can be driven with a relatively small voltage.
In this paper, a voltage-driven gradient coil with the conductive material distribution as a design variable, is proposed and optimized by the topology optimization method. Compared with the traditional stream function method, the proposed method avoids magnetic field deviations caused by the discrete approximation of coils. Optimal gradient coils have a much simpler pattern without windings of multi-turn wire. It is thereby possible to effectively reduce the length required for the gradient coil and improve the space utilization of the magnetic resonance system. The proposed method is suitable for designing the gradient coils of microscale MRI gradient coils. Even though the proposed method is still in its infancy, the preliminary design results have shown that it has advantages that the stream method cannot match.
There is still some work to do on further improving the optimization model. For example, multi-objective optimization of the gradient coils can be achieved by introducing other performances of the gradient coils, such as inductance and torque. A closed y-gradient coil can be obtained by adjusting the position of the input voltage.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] |