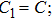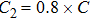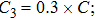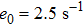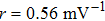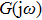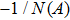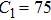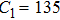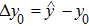† Corresponding author. E-mail:
Spontaneous alpha oscillations are a ubiquitous phenomenon in the brain and play a key role in neural information processing and various cognitive functions. Jansenʼs neural mass model (NMM) was initially proposed to study the origin of alpha oscillations. Most of previous studies of the spontaneous alpha oscillations in the NMM were conducted using numerical methods. In this study, we aim to propose an analytical approach using the describing function method to elucidate the spontaneous alpha oscillation mechanism in the NMM. First, the sigmoid nonlinear function in the NMM is approximated by its describing function, allowing us to reformulate the NMM and derive its standard form composed of one nonlinear part and one linear part. Second, by conducting a theoretical analysis, we can assess whether or not the spontaneous alpha oscillation would occur in the NMM and, furthermore, accurately determine its amplitude and frequency. The results reveal analytically that the interaction between linearity and nonlinearity of the NMM plays a key role in generating the spontaneous alpha oscillations. Furthermore, strong nonlinearity and large linear strength are required to generate the spontaneous alpha oscillations.
Alpha oscillation, defined as periodic fluctuations within the alpha band (8 Hz–12 Hz),[1] is ubiquitous in the brains of animals and humans.[2,3] Spontaneous alpha oscillations are observed in waking subjects and are most prominent in subjects that are relaxed with their eyes closed and otherwise mentally inactive. Since the first human electroencephalogram (EEG) recordings were performed by Hans Berger more than 90 years ago,[1] many studies have tried to establish correlations between the characteristics of alpha oscillations and cognitive processes.[4–19] Although several studies have shown that alpha oscillations are related to a wide range of basic and higher cognitive processes and play a functional role in both behavioral and neuronal responses, the mechanism of alpha oscillation generation is not fully understood.
Computational studies[20–25] are effective for elucidating the mechanism by which neural oscillations occur due to their ability to model complex neurological phenomena with relative ease.[26] In this context, many biophysical models have been developed to understand the generation of neural oscillation.[27–32] As a typical computational neural model, the neural mass model (NMM) was initially proposed to study the origin of the alpha rhythm based on a biologically plausible parameterization of the dynamic behavior of the layered neocortex.[33,34] Subsequently, the NMM has been improved and extended to model various cortical electrical activities.[35] Jansenʼs NMM is an extended version of the neural mass model that adds an excitatory feedback loop in parallel to the inhibitory feedback loop in the original version of the NMM.[36]
To date, Jansenʼs NMM (for simplicity of denotation, we will use NMM to refer to Jansenʼs NMM for the remainder of this paper) has been extensively used to study alpha oscillation mainly through numerical study, such as resonance and bifurcation analyses.[27] Resonance analyses are conducted by linearizing the sigmoid function in the NMM.[35] However, this produces a stimulus-induced alpha response and not a spontaneous oscillation, which is dominated by linear dynamics and reflect fluctuations about an equilibrium-state.[37] Most of bifurcation studies use the input of the NMM as a bifurcation parameter to study neural oscillation; therefore, the responses produced in these studies are also stimulus-dependent oscillations. Spontaneous alpha oscillation is related to limit cycle dynamics[27,28] and is primarily determined by the intrinsic properties of the NMM. Nonlinearity is the fundamental reason for the occurrence of limit cycles, however, it is not fully understood how the nonlinear part of the NMM interacts with its linear part to cause spontaneous alpha oscillations.
In the present study, we use the describing function method to analyse the spontaneous alpha oscillations in the NMM. Our main contribution is to propose an analytical method to accurately determine frequency and amplitude of the spontaneous neural oscillation. To do so, we take Jansen–Ritʼs neural mass model as an example to demonstrate the method. Our results suggest that the interaction between linearity and nonlinearity of the NMM plays a key role in generating spontaneous alpha oscillations and that, furthermore, strong nonlinearities and large linear strength are required. These results provide an insight into the mechanism of spontaneous alpha oscillations and the role of the linear and nonlinear parts in generating them. Additionally, these results provide testable hypotheses for future experimental studies.
Jansenʼs neural mass model describes a small local network representing a cortical region. As illustrated in Fig.
In the NMM, each population receives input in the form of an average postsynaptic membrane potential from the other neural populations and converts this membrane potential into an average firing rate. Therefore, each population is composed of the following two parts: an excitatory or inhibitory linear dynamic function 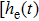
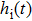
The impulse response functions of the excitatory and the inhibitory dynamic functions are given by the following equation[36]
The sigmoid function S(v) is described by the following equation:[38]
The parameter values of the NMM can be estimated from the empirical data,[34,36,39,40] and are shown in Table
| Table 1.
Physiological explanation and standard values of NMM parameters. . |
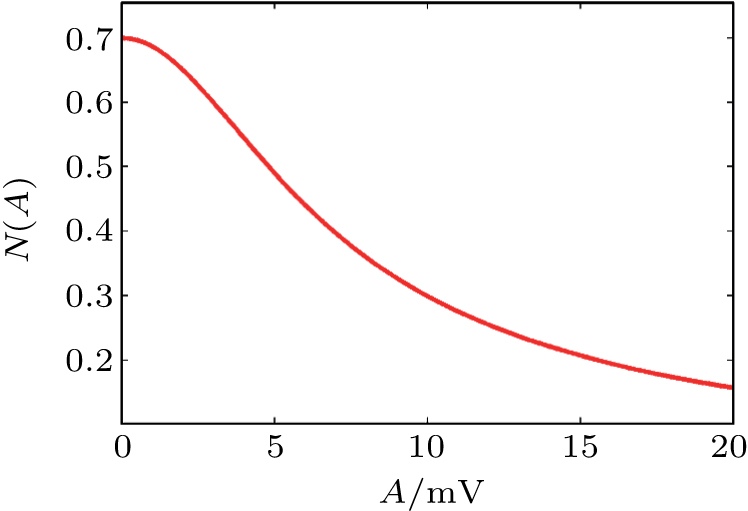
The describing function method is a nonlinear analysis method that is widely used to analyse spontaneous oscillations of nonlinear dynamical systems.[41] Recently, this method was used to analyse the mechanism of action of deep brain stimulation,[42] the behavior of a seizure neural mass model[43] and a model of deep brain stimulation.[44] The main principle of the describing function method is that in response to a sinusoidal input, most nonlinear system will produce a periodic signal (which is not necessarily sinusoidal) with the frequency being the harmonics of the input frequency. Therefore, the describing function can be viewed as an extension of the frequency response to nonlinearity, which can be approximated by a frequency-dependent equivalent gain.
Supposing that the input to a nonlinear function is 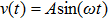
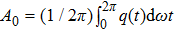
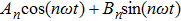
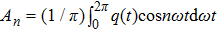
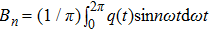
Because the linear part of a dynamical system is generally of low-pass, the high frequency component of q(t) decreases rapidly as the frequency increases. Thus the output q(t) of the nonlinear element can be approximated by the first fundamental component of this series and calculated as follows:[45]
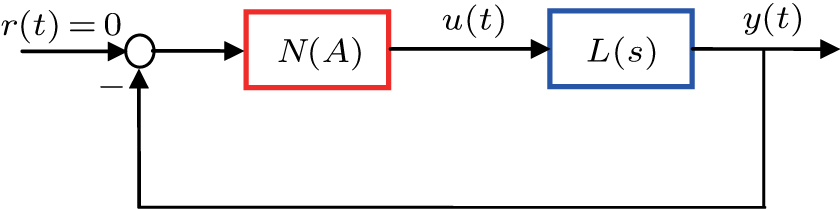
Within the theoretical framework of the describing function method, the block diagram of a nonlinear system is shown in Fig.
The characteristic equation of a nonlinear system (shown as in Fig.
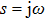
All simulation analyses were conducted using MATLAB software (
The simulation parameters of the NMM were set and described in Table
We used a variable-size simulation time-step with maxim step size 0.001 s. Initial conditions were set to be zero.
Nyquist diagrams were plotted using the MATLAB function “nyquist”.
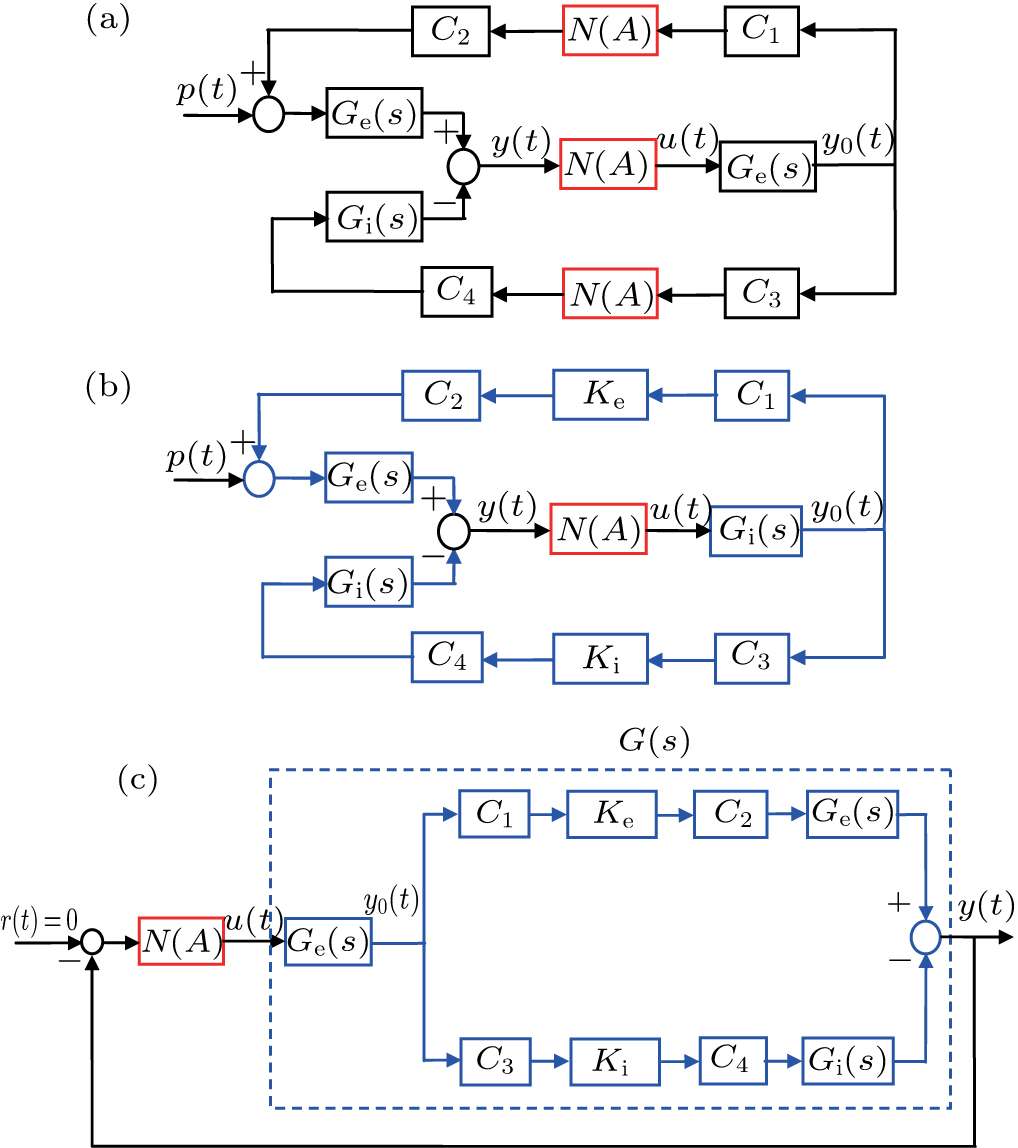
In this section, we use the describing function method to investigate the mechanisms underlying spontaneous alpha oscillations in the NMM. First, we reformulate the NMM (shown in Fig.
By conducting the Laplace transform with Eq. (
The sigmoid function S(v) in the NMM is odd symmetric; therefore, the coefficients of all the even parts are equal to zero, which means that 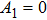
To use the describing function method to analyze spontaneous alpha oscillations in the NMM, we need to transform the NMM into the standard form of a nonlinear system (as shown in Fig.
First, we use N(A) to replace the three sigmoid functions S(v) in the NMM, which transforms Fig.
Second, we reformulate the NMM (shown in Fig. 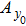


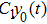
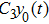
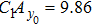

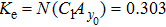

Third, we equivalently transform Fig.
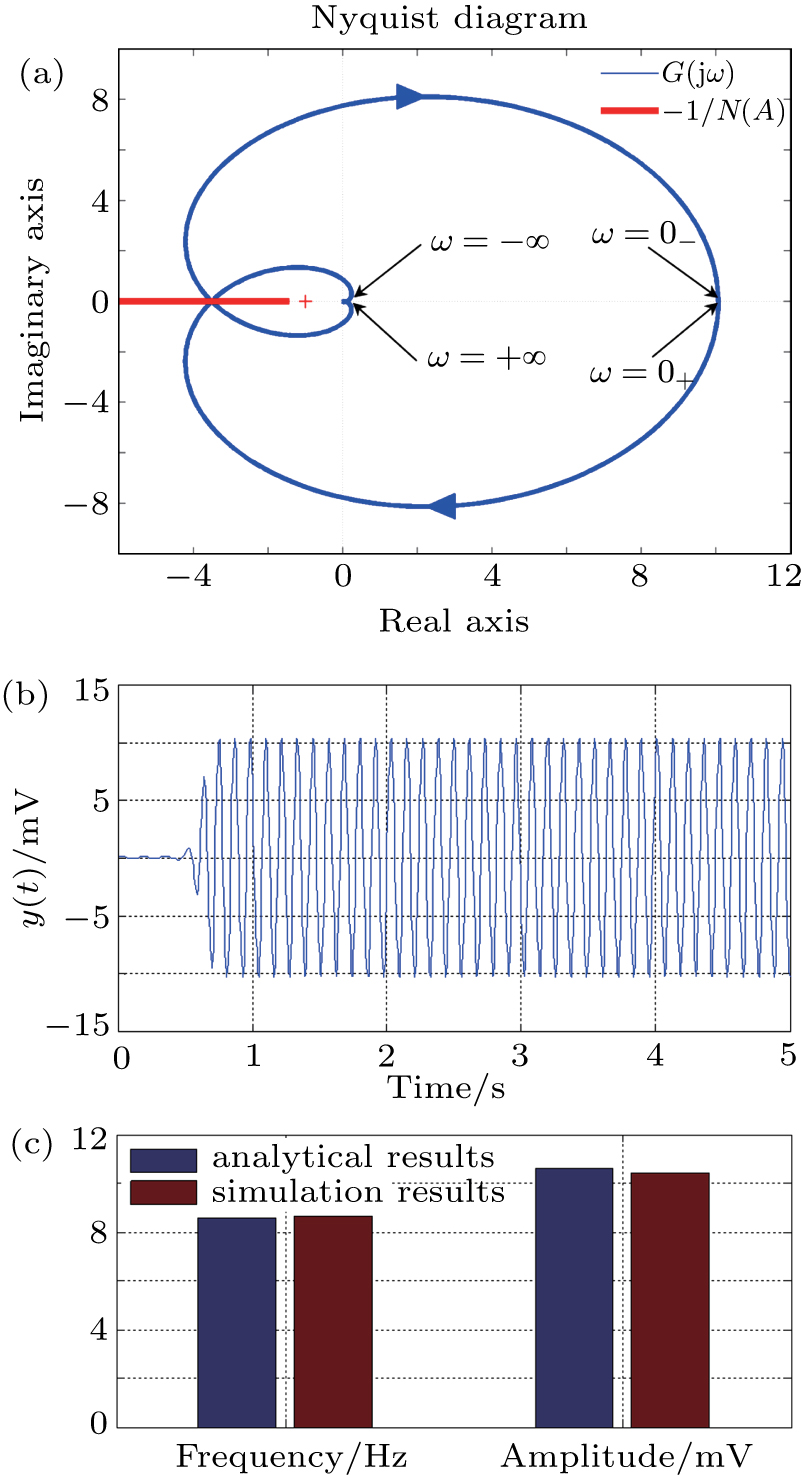
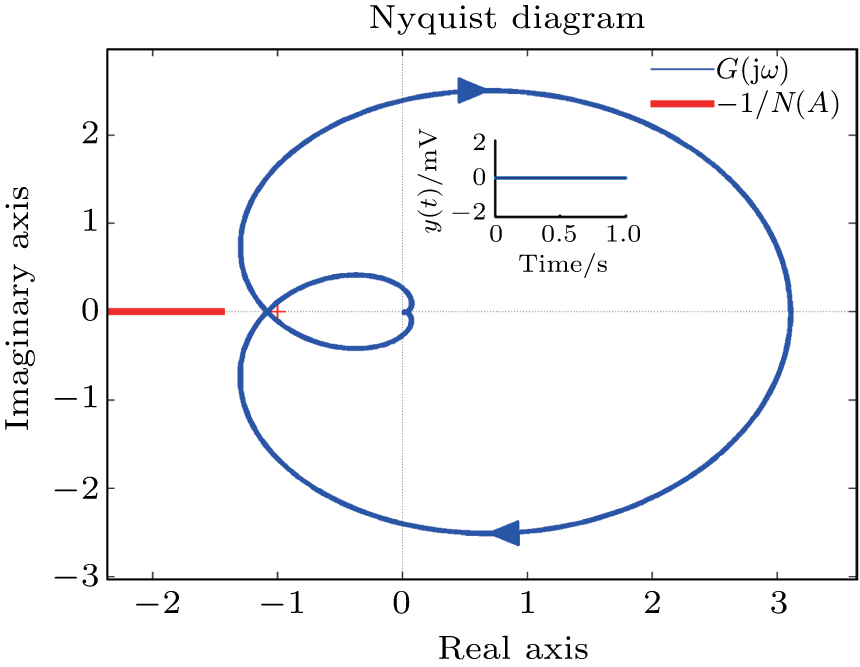
In this section, the Nyquist criterion can be extended to understand the behavior of the NMM whose nonlinearities have been approximated using the describing function.[45] According to Fig.
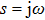
Usually, it is difficult to directly solve Eq. (
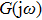

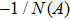
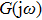
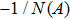
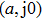
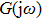

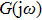
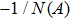
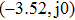
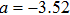
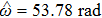
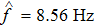
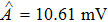
To verify the validity of the analytical results, we conduct time–domain simulations of the NMM using MATLAB software (for details see Section
A comparison between the analytical results and the simulation results is shown in Fig.
Figure 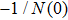
In this study, we use the describing function N(A) to approximate the sigmoid function S(v) in the excitatory and the inhibitory feedback loops. We estimate the amplitude of 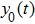
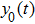
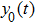
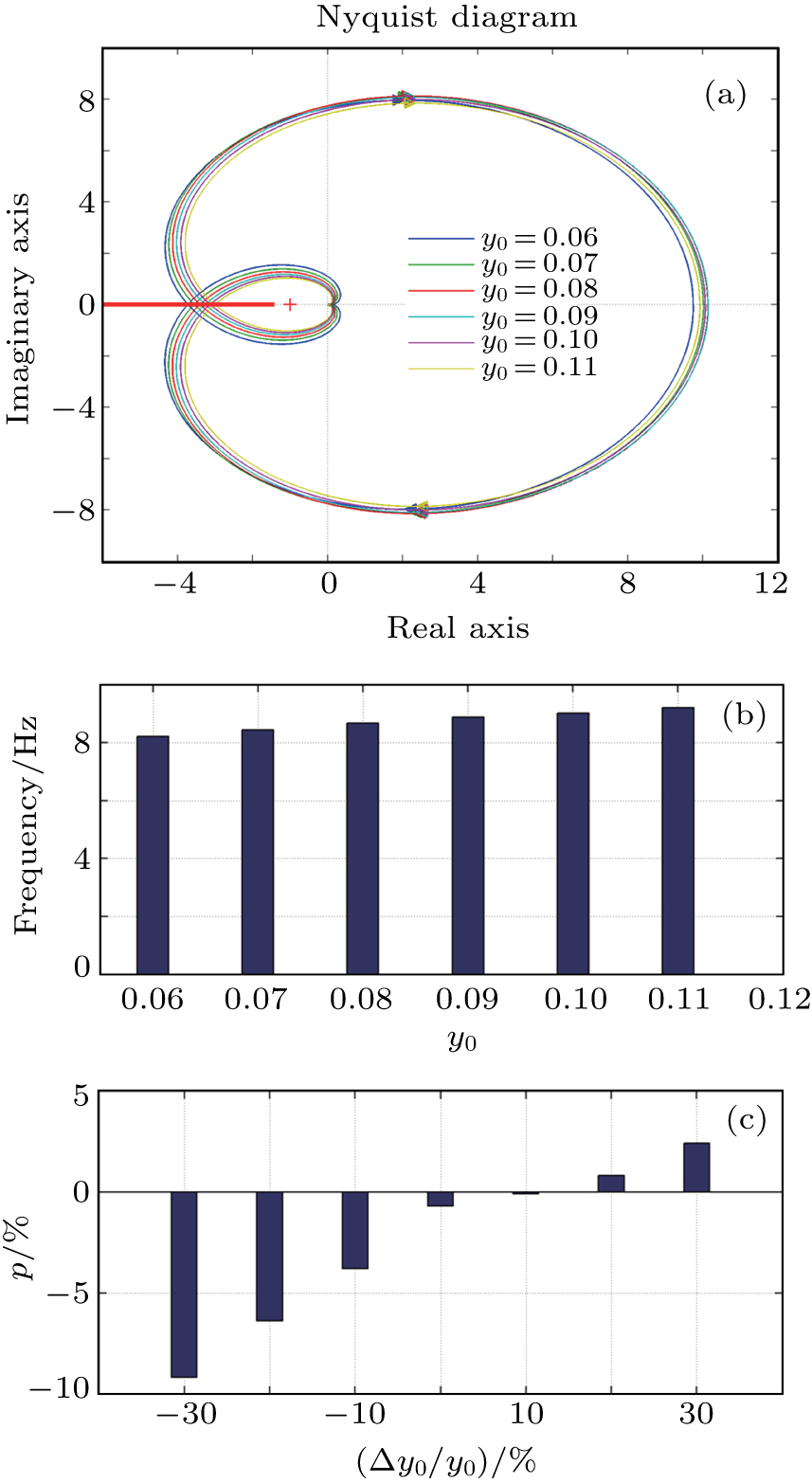
In this section, we discuss the effect of the model approximation error on the spontaneous oscillations in the NMM. To quantitatively evaluate the analytical precision, we define the analytical precision measure as 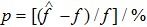
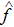
The analysis results are shown in Fig. 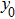
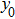
Figure 
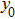
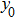
In the present study, we take a neural mass model as a test bed to demonstrate how to apply the describing function method to the analysis of the spontaneous alpha oscillations and determine their frequency and amplitude. The proposed method can be easily extended to other neuronal circuits.
For a large scale feedback neuronal circuit,[46] there often exists a delay in the signal pathway due to dynamical relaying[47] and signal propagation.[48,49] We can incorporate the delay into the transfer function of the linear part as shown in Fig.
Autaptic connection is a typical structural pattern, and provides a self-feedback loop for neuronal circuits.[50,51] Previous studies have revealed that autaptic connections have an important influence on neuronal dynamics[50,51] and information processing.[52] Within the describing function theoretical framework, we can analytically elucidate the role that autaptic connections play by combining it into the linear part of the feedback system.
As many studies demonstrated, normal oscillations provide a substrate for neuronal information processing, such as information transmission[53] and neuronal computation.[54] On the other hand, abnormal oscillations are related to pathological diseases, such as epilepsy[3,25,55–59] and Parkinsonʼs disease.[60] As is well known, the plasticity in neuronal circuits plays a central role in maintaining brain functions. Due to synaptic plasticity,[61] structural plasticity, and intrinsic plasticity, respectively, the parameters in the feedback loops of neuronal circuits, such as the coupling strength and connectivity parameters in the linear part, and the parameters in the sigmoid nonlinear unit, are often time-varying. The present study reveals that the describing function method can build a relationship between neural oscillations and the parameters in the feedback pathways of neuronal circuits including excitatory and inhibitory feedback, and self-feedback in the form of autaptic connections.[50,51] Thus the proposed method may bridge between these neural plasticity mechanisms of brain function and neuronal disease. In a disease state, the neural system may lose its stability and pathological oscillation results.[54,59,62] The proposed method can determine the transition condition from the stable state to the unstable state and the oscillation characteristics. Thus, the method has the potential to understand the dynamical transformation of brain neural activities, such as from the normal state to disease states.
In this study, we use the describing function method to analyse spontaneous alpha oscillations in the NMM. The results demonstrate that the describing function method is useful in determining whether or not spontaneous alpha oscillations occur and in accurately determining the amplitude and frequency of the oscillations. The results also highlight that the interaction between the linear part and nonlinear part of the NMM plays a critical role in generating the spontaneous alpha oscillations. Furthermore, strong nonlinearity and large linear strength are required to generate the spontaneous alpha oscillations.
This proposed analytical method can build the relationship between the frequency and amplitude of the spontaneous oscillation and the model parameters in a more transparent manner than the numerical methods employed in most computational studies. Therefore this approach can provide an insight into how the model parameters exert effects on the frequency and amplitude of the spontaneous neural oscillation. It thus has the potential to gain an in-depth insight into the mechanism under the spontaneous oscillations. To sum up, this analytical method provides a novel theoretical framework which can be extended to the study of spontaneous oscillations in other computational neural models. We will develop more examples in future work.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] |