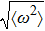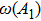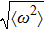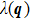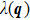† Corresponding author. E-mail:
Based on the first-principles density functional theory electronic structure calculation, we investigate the possible phonon-mediated superconductivity in arsenene, a two-dimensional buckled arsenic atomic sheet, under electron doping. We find that the strong superconducting pairing interaction results mainly from the pz-like electrons of arsenic atoms and the A1 phonon mode around the K point, and the superconducting transition temperature can be as high as 30.8 K in the arsenene with 0.2 doped electrons per unit cell and 12%-applied biaxial tensile strain. This transition temperature is about ten times higher than that in the bulk arsenic under high pressure. It is also the highest transition temperature that is predicted for electron-doped two-dimensional elemental superconductors, including graphene, silicene, phosphorene, and borophene.
Recently there has been a surge of interest in the investigation of two-dimensional (2D) superconductors, partially due to their potential application in nano-superconducting devices.[1,2] A pure 2D electronic system can be obtained by growing a single layer graphite or other materials on a proper substrate. The interplay between a 2D superconductor and the substrate has proven to be an efficient way to enhance superconductivity. For example, the superconducting transition temperature, Tc, of a single layer FeSe film deposited on the (001) surface of SrTiO3 is greatly enhanced[3,4] in comparison with the bulk FeSe superconductor,[5] resulting from the coupling between electrons and the phonon modes in the substrate.[6]
Superconductivity in graphene, which is the first 2D compound synthesized at laboratory, was extensively explored. Through a plasmon-mediated mechanism, Uchoa et al. discussed properties of superconducting states in several metal coated graphenes.[7] First-principles density functional theory (DFT) calculations predicted that the monolayer LiC6 and CaC6 are phonon-mediated superconductors with Tc of 8.1 K and 1.4 K, respectively.[8] Later, the superconducting phase was observed experimentally below 7.4 K in a Li-intercalated graphite thin film[9] and 6 K in a Ca-decorated graphene.[10] Calculations of electron-phonon interactions suggested that Tc of graphene can reach 23.8 K or even 31.6 K upon heavy electron or hole doping under 16.5% biaxial tensile strain (BTS),[11] but experimental evidence for such high-Tc superconductivity in doped graphenes is still not available.
In recent years, several new 2D materials, like silicene, phosphorene, and borophene, were synthesized experimentally. Similar to graphene, phosphorene is obtained by mechanically exfoliating layered black phosphorus.[12] Silicene[13,14] and borophene[15,16] were epitaxially grown on Ag (111) surfaces. It was reported that there is a charge transfer from the Ag (111) substrate to silicene[17] or borophene.[16] Furthermore, the substrate imposes strain to these single-layer materials, due to the lattice mismatch.[16,18–20] These effects of the substrate should be taken into account in the investigation of superconducting properties in these materials.
The DFT calculation also showed that the superconducting transition temperature can reach 16.4 K in silicene upon electron doping of n2D = 3.51 ×1014cm−2 and 5%-BTS.[21] Tc of phosphorene was predicted to be 12.2 K under the doping of 2.6×1014cm−2 and 8%-uniaxial tensile strain along the armchair direction.[22] Applying 4%-BTS to phosphorene can further increase Tc to 16 K.[23]
Unlike silicene and phosphorene, borophene is intrinsically a metal.[16] A free-standing pristine borophene is predicted to superconduct around 20 K,[24,25] especially for the χ3-type borophene whose Tc can be 24.7 K.[25] This is the highest superconducting transition temperature among predicted or observed 2D elemental superconductors without doping. Unfortunately, the charge transfer and tensile strain imposed by the Ag substrate suppress the superconducting order dramatically.[25,26]
Recently, a buckled single-layer honeycomb arsenic, i.e., arsenene, was proposed.[27,28] Unlike the semi-metallic bulk gray arsenic, arsenene is a semiconductor with an indirect energy gap of 2.49 eV. More importantly, arsenene undergoes an intriguing indirect-to-direct gap transition by applying a small BTS. This makes arsenene a promising candidate of transistor with high on/off ratios, optoelectronic device working under blue or UV light, and 2D crystal-based mechanical sensor.[27] Furthermore, it was predicted that arsenene has a higher electron mobility than that of MoS2,[29] and can become a unique topological insulator under suitable BTS without considering any spin-orbit coupling.[30]
In this work, we employ the first-principles DFT and the Wannier interpolation technique to accurately determine the electron–phonon coupling (EPC) properties of electron-doped arsenenes. The phonon-mediated superconducting Tc is evaluated based on the McMillian–Allen–Dynes formula. Without applying BTS, 0.1 electrons/cell (hereafter e/cell) doping can already turn arsenene into a superconductor with a superconducting temperature above the liquid-helium temperature. Tc increases to 10 K at 0.3 e/cell doping (i.e., n2D=2.76 ×1014cm−2). Moreover, we find that the A1 phonon mode at the K point contributes mostly to the EPC constant. From the electronic point of view, the pz-like electronic orbitals of arsenic atoms couple strongly with phonons. By applying a BTS, the A1 phonon mode is softened and the EPC matrix elements are enhanced. This enlarges both the EPC λ and the superconducting transition temperature. Under a 0.2 e/cell doping and 12% BTS, Tc of arsenene is predicted to be about 30.8 K. To the best of our knowledge, this is the highest Tc predicted for 2D elemental superconductors upon electron doping.
In the DFT-based electronic structure calculation, the plane wave basis method is adopted.[31] We calculate the Bloch states and the phonon perturbation potentials[33] using the local density approximation and the norm-conserving pseudopotentials.[32] The kinetic energy cut-off and the charge density cut-off are taken to be 80 Ry (1Ry=13.6056923(12)eV) and 320 Ry, respectively. A slab model is used to simulate arsenene, in which a 12-Å vacuum is added to avoid the interaction between the neighboring arsenic sheets along the c axis. Electron doping is simulated by adding electrons into the system with a compensating background of uniform positive charges. For each doping concentration, the atomic positions are relaxed but with fixed in-plane lattice constants which are obtained by optimizing the lattice structure of arsenene without doping.
The charge density is calculated on an unshifted mesh of 60×60×1 points, with a Methfessel–Paxton smearing[34] of 0.02 Ry. The dynamical matrix and perturbation potential are calculated on a 
The EPC constant λ is determined by the summation of the momentum-dependent coupling constant 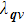
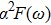
 |




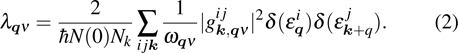 |

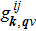
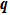




 |
We calculate the superconducting transition temperature using the McMillian–Allen–Dynes formula,[43]
 |
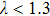
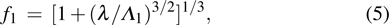 |
 |
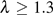

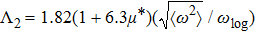
 |
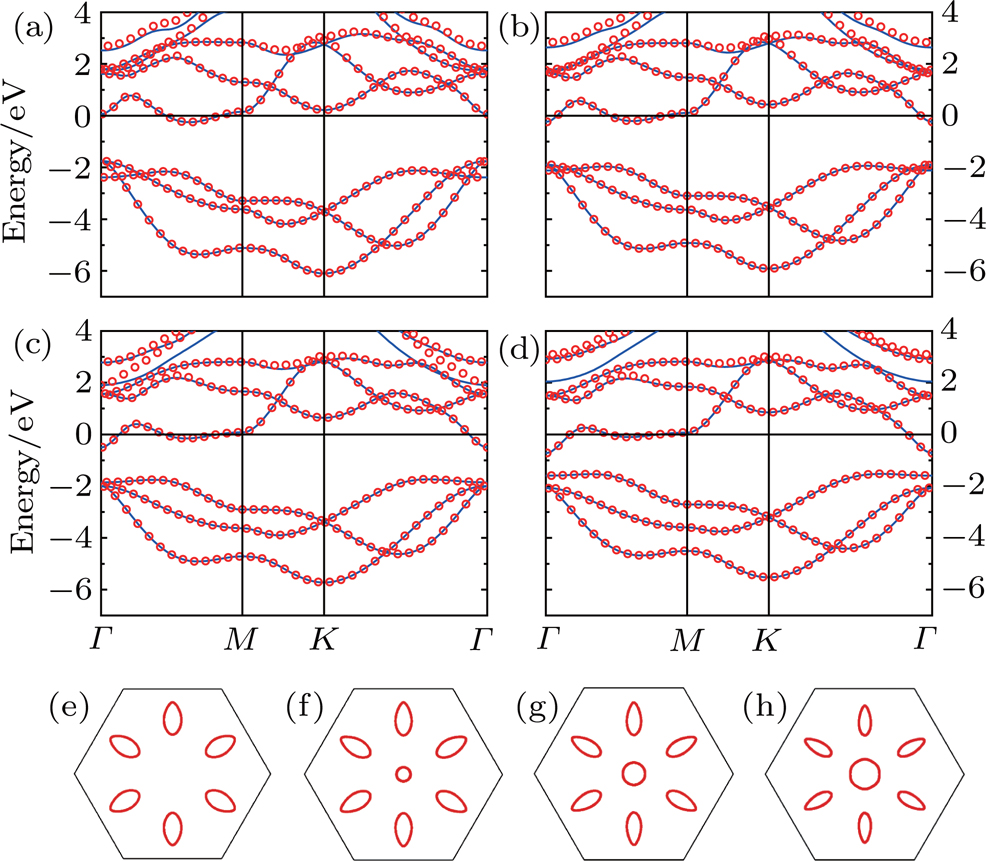
For a free standing arsenene without doping, we find that the optimized lattice constant is 3.5411 Å, in agreement with the result, 3.5408 Å, obtained by Zhang et al.[27] Our calculation shows that arsenene is semiconducting with an indirect band gap of 1.42 eV. The valence band maximum is at the Γ point, while the conduction band minimum is located on the line between Γ and M. Although the energy gap is underestimated in comparison with the HSE06-level result,[27] it does not affect our EPC results since the shapes of conduction band given by LDA and HSE06 are concordant.
Figure
Figure
The Eliashberg spectral function 
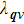
 | Fig. 3. (color online) Frequency dependence of the Eliashberg spectral function 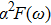
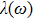
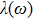

|
Based on the above results, we calculate the superconducting transition temperature Tc using the McMillian–Allen–Dynes formula.[43] The results, together with other key parameters, are presented in Table
| Table 1.
Predicted superconducting transition temperature Tc and other parameters obtained by the first-principles calculation at various doping (e/cell) and BTS ε (%): N(0), frequency of A1 phonon |
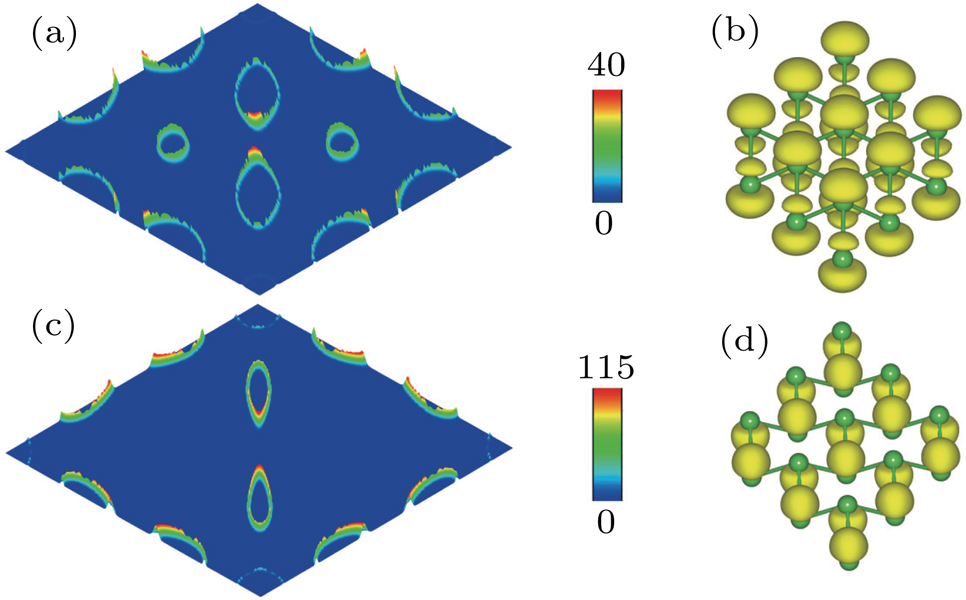
The EPC constant λ is determined by the DOS, the phonon frequency 
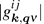
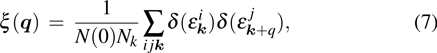 |
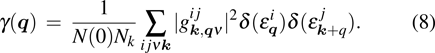 |


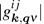
Figure 
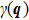



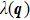

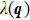
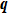

The BTS is measured by 
At 4% BTS, as shown in Fig.
Figure
 | Fig. 6. (color online) Phonon spectra of arsenenes under (a) 2%, (b) 4%, (c) 6%, and (d) 8% BTS. The amplitude of 
|
When the applied BTS is less than 4%, the two-peak structures of 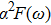
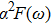
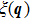

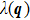

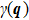
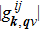
 | Fig. 7. (color online) Eliashberg spectral function 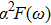

|
To determine which electron band contributes most to the EPC, we calculate 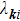
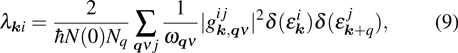 |



For all the cases we have studied, we find that 

The maximal superconducting Tc of 23.8 K is predicted for 4.65×1014 cm−2 electron-doped graphene under 16.5% BTS. Realistically, realizing such requirements in graphene may be very difficult in experiment. The advantage in the case of arsenene is that the high-Tc superconductivity above 30 K may be obtained under a relatively smaller doping density (1.28×1014 cm−2) and BTS (12%). Recently, multilayer arsenenes were successfully grown on InAs using the plasma-assisted process.[46] The bulk gray arsenic, which is the most stable phase among all arsenic allotropes,[47] could be used as a precursor to prepare arsenene.[27,28] By growing arsenene on a piezoelectric substrate, one can control BTS by applying a bias voltage to elongate or shorten the lattice constants.[19] The electron doping can be achieved either by chemical doping or substitution, or by liquid or solid gating.[48,49] Thus it is feasible to verify our prediction experimentally.
Based on the first-principles DFT electronic structure calculation, we predict that the semiconducting arsenene can become a phonon-mediated superconductor upon doping of electrons. The maximal superconducting transition temperature is found to be around 10 K in the doped arsenene. It can be further lifted to 30 K by applying a 12% BTS. The superconducting pairing results mainly from the A1 phonon mode around the K point and the pz-like electrons of arsenic atoms.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] |