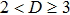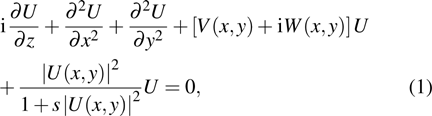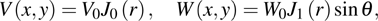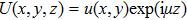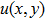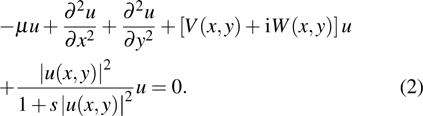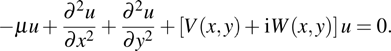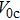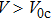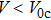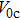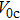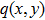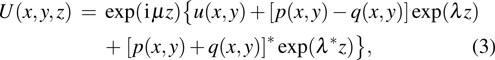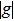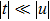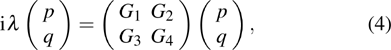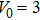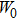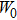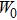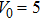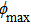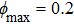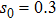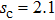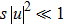Fundamental and dressed annular solitons in saturable nonlinearity with parity–time symmetric Bessel potential
School of Electrical Engineering and Intelligentization, Dongguan University of Technology, Dongguan 523808, China
† Corresponding author. E-mail:
wanghc@dgut.edu.cn
1. IntroductionOptical spatial solitons are self-trapped beams which can propagate in nonlinear medium without changing intensity profiles due to the balance among nonlinearity, diffraction, and optical potential.[1,2] Due to their intriguing physical properties and their potential applications, lots of theoretical and experimental efforts have been made to investigate the propagation dynamics and optical steering of various kinds of spatial solitons.[3] The introduction of optical lattices into a nonlinear medium significantly promotes the research on soliton phenomena in optics[4,5] and other physics fields.[6] Among all kinds of optical lattices, Bessel lattices have received special attention because such lattices have unique radial profiles which obey the patterns of Bessel function and they can suppress optical diffraction for the lattice-inducing field. The unique cylindrical symmetry of such an optical lattice allows the stable ring, vortex,[7] multi-dipole,[8] spatiotemporal solitons,[9] and necklace solitons[10] to exist. Interestingly, rotary (dipole) solitons were predicted to reside on different rings of Bessel lattices in a focusing cubic nonlinear medium[11] while light guided by Bessel-like lattices with a low refractive-index core was observed.[12]
In fact, wave-propagation models can naturally be divided into two generic classes, i.e., conservative and dissipative. All these studies about the Bessel lattices mentioned above were focused on the real potentials and they were studied in the frame of conservative models.
A new avenue for exploring various wave phenomena has recently been opened up by appropriately choosing spatial distributions of both gain and loss. Such non-Hermitian Hamiltonian systems can give rise to novel wave effects that are impossible to realize with conventional Hermitian potentials. In particular, optical systems each with a so-called parity–time (PT) symmetry where gain and loss are carefully balanced, have recently attracted enormous interest in the context of non-Hermitian photonics.[13] The concept of PT symmetry started out from quantum mechanics, where it was observed that complex potentials with parity–time symmetry could still exhibit all-real spectra even though the underlying Schrödinger operator is non-Hermitian.[14] Later, this concept spread to optics, where it was realized that the optical waveguides with even refractive-index profiles and odd gain-loss distributions constitute PT-symmetric systems.[15,16]
The realization of complex PT-symmetric potentials within the framework of optics has paved the way towards several novel optical control schemes with intriguing and unexpected properties.[17] In addition to optical switching, the topic of nonlinear self-focusing and the formation of self-localized solitons received strong attention. So far, optical solitons have been found in nonlinear media with various PT-symmetric potentials, such as PT-symmetric periodical potential,[16,18,19] Gaussian potential,[20] parabolic potential, Scarff potential,[21] superlattice,[22,23] etc. Recently, fundamental, dipole, and multi-peak solitons have been found to exist in PT-symmetry Bessel linear potential[24] and mixed Bessel linear potential and modulated nonlinear lattices,[25] respectively. When a defect is present in the parity–time symmetric Bessel potential, fundamental solitons can also exist and propagate stably, while dipole solitons are stable only at low powers.[26] In the two-dimensional case, linear modes, fundamental and dipole solitons were discussed in PT symmetric Bessel complex-valued potential.[27] Stable vortex solitons were also addressed in partially-PT-symmetric continuous azimuthal potentials from fully-PT-symmetric cells placed on a ring.[28,29] Very recently, strongly nonlocal nonlinear media with PT-symmetric potential in fractional dimension
 were found to be able to support the localized accessible soliton family.[30] The aim of this paper is to study the existence and stability of fundamental and “dressed” annular solitons in PT-symmetric Bessel lattices. The “dressed” annular soliton seems to be a fundamental soliton dressed with a single ring. The discovery of this novel type of soliton can enrich the types of optical solitons.
were found to be able to support the localized accessible soliton family.[30] The aim of this paper is to study the existence and stability of fundamental and “dressed” annular solitons in PT-symmetric Bessel lattices. The “dressed” annular soliton seems to be a fundamental soliton dressed with a single ring. The discovery of this novel type of soliton can enrich the types of optical solitons.
2. Theoretical modelWe consider the evolution of paraxial beams in self-focusing saturable nonlinearity with two-dimensional PT-symmetric Bessel optical lattice, which is described by the following dimensionless nonlinear Schrödinger equation:
where
U is the slowly varying amplitude of the beam,
s is the saturable coefficient,
z is the normalized longitudinal coordinate, while
x and
y are the normalized coordinates along the transverse directions. For 2D PT-symmetric Bessel optical lattices, the real and imaginary parts of the complex potential can be described by
where
V0 and
W0 are the modulation depths of the real and imaginary parts of PT-symmetric Bessel potentials, and
r and
θ are the radial and angular coordinates, respectively. Because of the presence of the imaginary part in the complex potential, the soliton solution should be complex, i.e., the optical field should be complex. To form solitons, the beams should carry special phase structures in PT-symmetric potentials. In optical lattices without imaginary potentials, the phase of a fundamental soliton is uniform and a vortex soliton only carries a vortex phase. When
, the potential can degenerate into a real model without PT-symmetry.
As the experimental implementation of the model, radially symmetric Bessel lattices can be induced by non-diffracting Bessel beams in a slow Kerr-type medium, resonant systems such as atomic gases,[31] or artificially designed metamaterials. As described in Ref. [31], PT-symmetric refractive index landscapes can be imprinted in a cold gas of two atomic isotopes in a Λ-type configuration (e.g., 87Rb and 85Rb isotopes) loaded in an atomic cell. Different order Bessel beams can be created by illuminating a narrow annular slit placed in the focal plane of a lens or axicon[32] or by using holographic techniques.[33]
To check the existence of fundamental and “dressed” solitons, we search for the stationary solutions of Eq. (1) in the form of
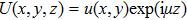 , where μ is the propagation constant and
, where μ is the propagation constant and
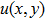 is a complex-value localized function. Substitution of this stationary solution into Eq. (1) directly leads to the following equation:
is a complex-value localized function. Substitution of this stationary solution into Eq. (1) directly leads to the following equation:
To ensure that the PT-symmetry does not break, we should investigate the linear case to check the PT-symmetry breaking points. Adopting a similar method to that in Ref. [
16], we investigate the eigenvalues and the eigen spectrum of potential to determine the phase transition point. At the phase transition point, an infinite number of eigenvalues become complex simultaneously. Above the phase transition point, the spectrum is no longer purely real as the strength of the imaginary (gain-loss) contribution relative to the real (refractive-index) contribution in the potential is increased. To study the phase transition point, we give the linear version of Eq. (
1), which can read as
By solving this linear equation, we can obtain the eigenvalues and the corresponding linear modes of the potential for different values of
V0 and
W0. For each
W0 value, there exists a critical value
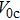
. When
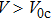
, all the eigenvalues of the potential are purely real and PT-symmetric linear modes can be obtained. While
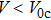
, complex eigenvalues appear. Therefore, the critical value
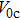
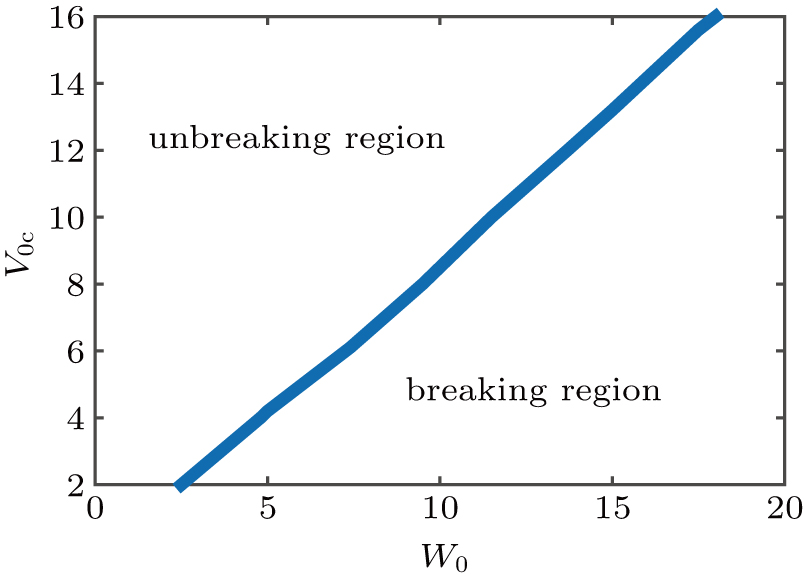
is the phase transition point of PT-symmetry breaking. Figure
1 shows the plot of PT-symmetry breaking point versus
W0. It can be found that PT-symmetry breaking point
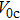
increases almost linearly as
W0 increases. Therefore, we confine our investigation on those values of
V0 and
W0 in the PT-symmetry unbreaking region hereafter.
Soliton solutions can be obtained by solving Eq. (2) through using the modified squared-operator iteration method. The power is defined as
 . In order to investigate the linear stability of optical solitons, we add the perturbations
. In order to investigate the linear stability of optical solitons, we add the perturbations
 and
and
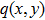 into the solution, which is written as
into the solution, which is written as
where
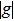
,
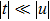
, and the superscript “*” represents the complex conjugation. Substituting Eq. (
3) into Eq. (
1) and linearizing the resulting equation, we can acquire the following coupled equations:
where
Equation (4) can be solved by the Fourier collocation method, and the complex value λ can be obtained. If
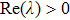 , the solitons are linearly unstable; otherwise they are linearly stable.
, the solitons are linearly unstable; otherwise they are linearly stable.
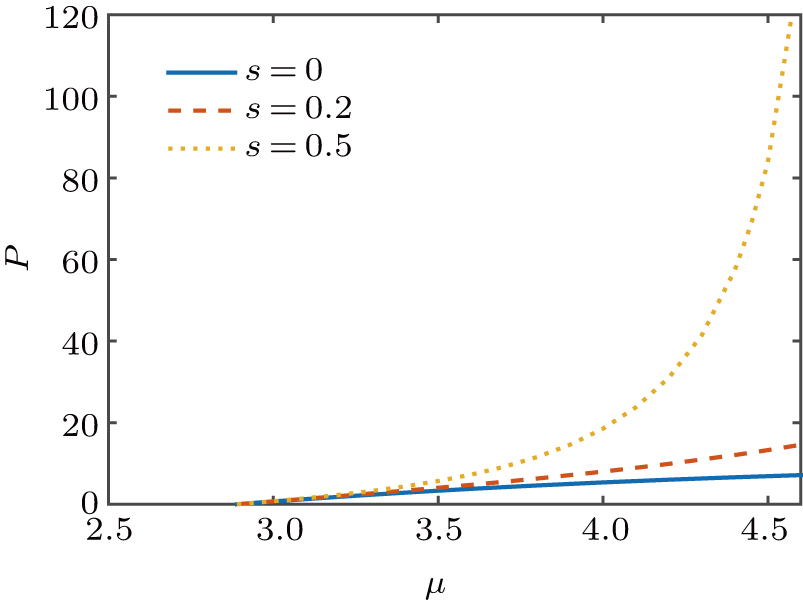
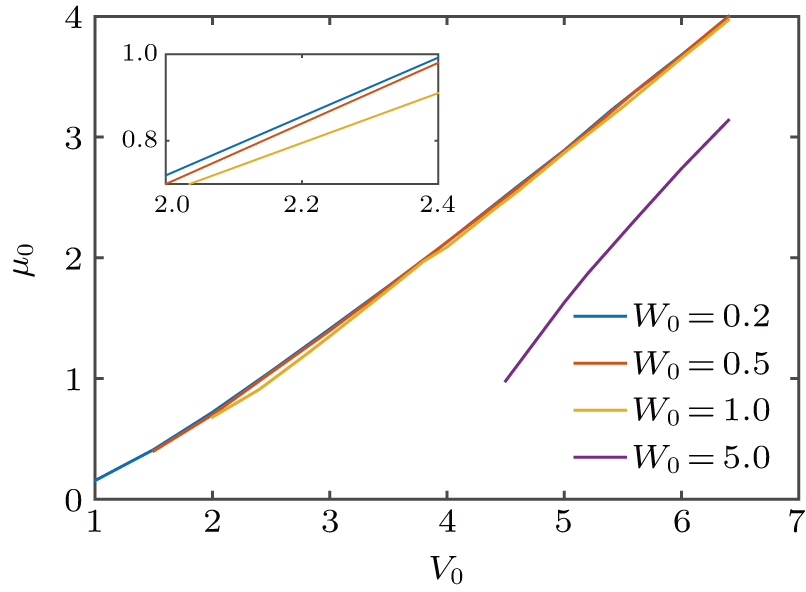
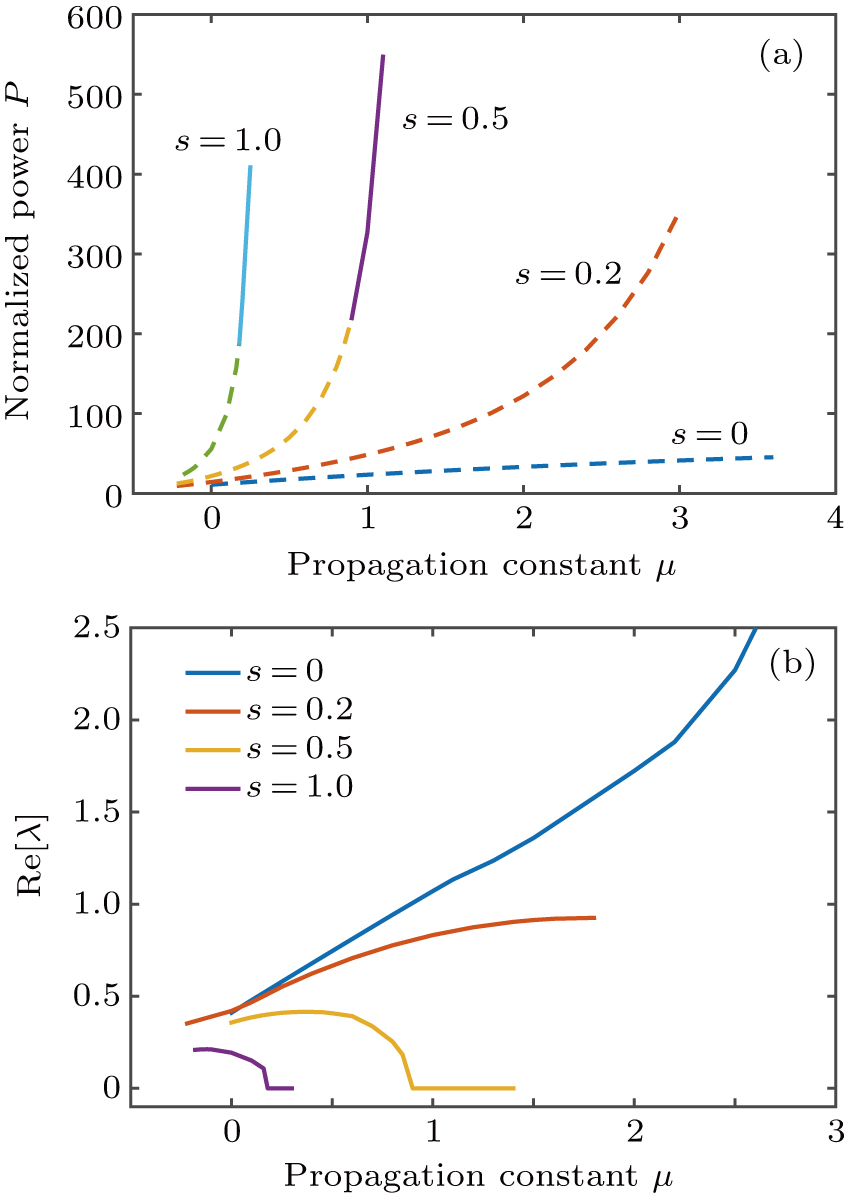
3. Soliton solutions3.1. Fundamental solitons and their stabilityIn this section we discuss the existence and stability of fundamental solitons in self-focusing saturable nonlinearity with a PT-symmetric Bessel optical lattice. For the convenience of demonstration, we set the saturable parameter s = 0, 0.2, and 0.5, respectively. The corresponding power diagram versus the propagation constant μ is displayed in Fig. 2. From Fig. 2, one can see that the power of fundamental solitons increases monotonically with μ increasing. Furthermore, a larger saturable parameter leads to a larger power value of fundamental solitons for a fixed propagation constant. The existence curve of fundamental solitons becomes very steep when μ gets a large value. It is due to the fact that the large saturable parameter weakens the focusing nonlinearity. Then, it needs larger power to compensate for this nonlinearity and to balance the diffraction induced by the complex potential. It is found that the fundamental solitons can exist only when μ is above the critical value μ0. Figure 3 shows that the value of μ0 depends on the values of V0 and W0. For a fixed W0, the critical propagation constant
 increases monotonically with V0 increasing. Figure 4 shows the relations between μ0 and W0 for the cases of
increases monotonically with V0 increasing. Figure 4 shows the relations between μ0 and W0 for the cases of
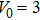 and 5. For a fixed V0, μ0 decreases monotonically as the value of
and 5. For a fixed V0, μ0 decreases monotonically as the value of
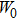 increases. In other words, a high W0 value leads to a small μ0 value. For low values of W0, the effect of
increases. In other words, a high W0 value leads to a small μ0 value. For low values of W0, the effect of
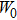 on μ0 is relatively small. When
on μ0 is relatively small. When
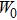 approaches to the PT-symmetry breaking point, μ0 decreases quickly as W0 increases. For the convenience of describing the existence and stability of fundamental solitons and dressed solitons, we set
approaches to the PT-symmetry breaking point, μ0 decreases quickly as W0 increases. For the convenience of describing the existence and stability of fundamental solitons and dressed solitons, we set
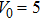 and
and
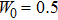 hereafter, and we have
hereafter, and we have
 . By solving Eq. (4) numerically, we find that all the real parts of eigenvalue λ are zero or below zero. Therefore, it can be concluded that all the fundamental solitons are stable in the whole existing region.
. By solving Eq. (4) numerically, we find that all the real parts of eigenvalue λ are zero or below zero. Therefore, it can be concluded that all the fundamental solitons are stable in the whole existing region.
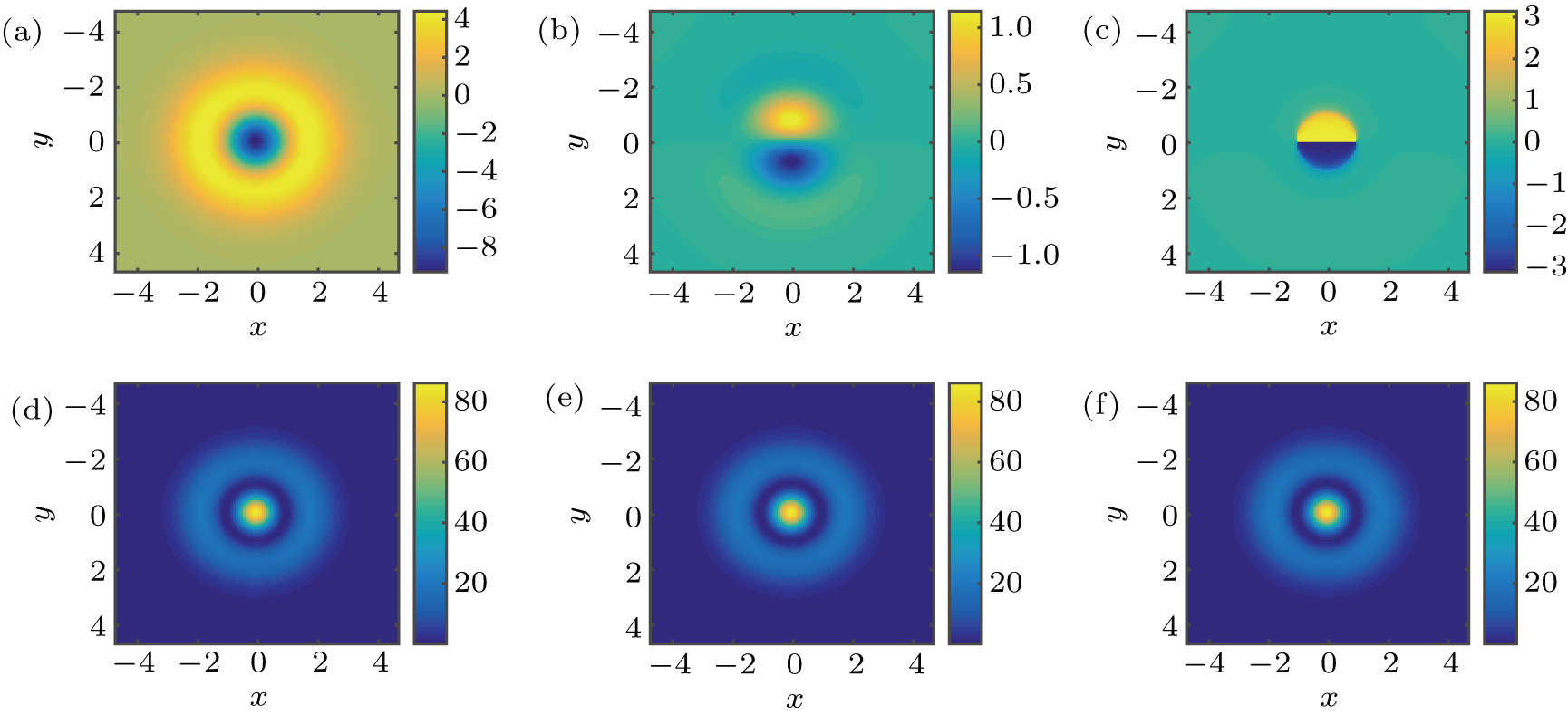
To demonstrate the propagation stability of fundamental solitons, we take μ =4 and s = 0.5 as a typical example. Because of the presence of the PT-symmetric potential, the fundamental soliton solution is also PT-symmetric. Figure 5(a)–5(d) depict the real part, imaginary part, the phase structure and the intensity profiles. We can see that the real part of the optical field has a Gaussian-like profile while the imaginary part has two humps with a special phase structure. The real part is symmetric while the imaginary part is asymmetric. The complex optical field always leads to a non-uniform distribution in the phase structure. For fundamental solitons in PT-symmetric Bessel lattices, the phase is nonzero in the whole region of optical field except in the center of the fundamental soliton. Because the value of the imaginary part of the potential is much lower than that of the real part, the maximum value of the phase
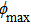 is relatively small. When μ =4 and s = 0,
is relatively small. When μ =4 and s = 0,
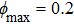 [Fig. 5(c)]. From Fig. 5(d), one can see that the fundamental solitons have a single hump sited on the center of the potential, with a special phase structure. To validate the stability results obtained by the perturbation theory, we add 1% random noises to the numerical solution of the fundamental solitons, and the intensity profile of the perturbated soliton is shown in Fig. 5(e). After 500 dimensionless propagation lengths, the solitons can still keep their intensity profile and propagate stably as shown in Fig. 5(f).
[Fig. 5(c)]. From Fig. 5(d), one can see that the fundamental solitons have a single hump sited on the center of the potential, with a special phase structure. To validate the stability results obtained by the perturbation theory, we add 1% random noises to the numerical solution of the fundamental solitons, and the intensity profile of the perturbated soliton is shown in Fig. 5(e). After 500 dimensionless propagation lengths, the solitons can still keep their intensity profile and propagate stably as shown in Fig. 5(f).
3.2. “Dressed solitons” and their stabilityIn this section, we introduce a novel type of optical soliton, named the “dressed soliton,” whose intensity profile has a ring dressed on an intensity hump. To the best of our knowledge, this is completely new because it has never been reported before. In addition to the difference between their intensity profiles, the phase structures of dressed annular solitons are also completely different from those of fundamental solitons. The real part of the optical field of a dressed soliton is circularly symmetric, while the imaginary part is anti-symmetric and it populates in the central region only. Therefore, there is a special phase structure in the region of the central intensity hump, i.e., a
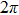 phase jump in the center. In other regions including the surrounding ring of the intensity profiles, the phase is always near zero. Figure 6 shows the dependence of normalized power and the corresponding instability growth rate of white noises on the propagation constant μ for the cases of saturable parameter s = 0, 0.2, 0.5 and 0.8. It is found that for each saturable parameter s, there exists a threshold value of power, below which no dressed solitons can be found. From Fig. 6, one can see that the dressed solitons are unstable in a nonlinear medium with parity–time symmetry for low saturable parameter s. For s = 0 and s = 0.2, the instability growth rate increases as the propagation constant increases, and all the dressed solitons are unstable in their whole existence regions. When s = 0.5 and s = 1.0, the instability growth rate keeps a nonzero value at low values of μ. As we further increase the value of μ, the real part of λ decreases to zero rapidly. When μ is higher than a critical value, the real part of λ is always zero and the solitons are always stable. It means that the dressed solitons are stable in the high power regions, while they are unstable in the lower power regions. This is completely different from other solitons in the PT-symmetric optical lattices with cubic nonlinearity, in which optical solitons with low powers are stable but high power solitons are unstable.[19] This indicates that the dressed solitons can be stable for high values of saturable parameter, and the saturable nonlinearity helps stabilize the propagation of dressed solitons. Besides, dressed solitons have higher power and lower values of instability growth rate in the nonlinear medium with higher saturable parameter for a fixed propagation constant. Numerical simulations show that the stable dressed solitons can be found only when the saturable parameter is above a threshold, which has been shown at
phase jump in the center. In other regions including the surrounding ring of the intensity profiles, the phase is always near zero. Figure 6 shows the dependence of normalized power and the corresponding instability growth rate of white noises on the propagation constant μ for the cases of saturable parameter s = 0, 0.2, 0.5 and 0.8. It is found that for each saturable parameter s, there exists a threshold value of power, below which no dressed solitons can be found. From Fig. 6, one can see that the dressed solitons are unstable in a nonlinear medium with parity–time symmetry for low saturable parameter s. For s = 0 and s = 0.2, the instability growth rate increases as the propagation constant increases, and all the dressed solitons are unstable in their whole existence regions. When s = 0.5 and s = 1.0, the instability growth rate keeps a nonzero value at low values of μ. As we further increase the value of μ, the real part of λ decreases to zero rapidly. When μ is higher than a critical value, the real part of λ is always zero and the solitons are always stable. It means that the dressed solitons are stable in the high power regions, while they are unstable in the lower power regions. This is completely different from other solitons in the PT-symmetric optical lattices with cubic nonlinearity, in which optical solitons with low powers are stable but high power solitons are unstable.[19] This indicates that the dressed solitons can be stable for high values of saturable parameter, and the saturable nonlinearity helps stabilize the propagation of dressed solitons. Besides, dressed solitons have higher power and lower values of instability growth rate in the nonlinear medium with higher saturable parameter for a fixed propagation constant. Numerical simulations show that the stable dressed solitons can be found only when the saturable parameter is above a threshold, which has been shown at
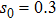 . For a fixed saturable parameter s, the power of the dressed solitons increases quickly with the increase of propagation constant μ. This can be explained as follows. Because a large staturable parameter can weaken the focusing nonlinearity effect, larger power is necessary for enhancing the nonlinearity and balancing the diffraction in higher saturable nonlinearity. However, there exists a threshold of saturable parameter for the existence of dressed solitons, above which the dressed solitons cannot be found. In this model, it is found that the threshold saturable parameter is
. For a fixed saturable parameter s, the power of the dressed solitons increases quickly with the increase of propagation constant μ. This can be explained as follows. Because a large staturable parameter can weaken the focusing nonlinearity effect, larger power is necessary for enhancing the nonlinearity and balancing the diffraction in higher saturable nonlinearity. However, there exists a threshold of saturable parameter for the existence of dressed solitons, above which the dressed solitons cannot be found. In this model, it is found that the threshold saturable parameter is
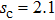 . For extremely large values of s, the term
. For extremely large values of s, the term
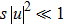 and the nonlinear term, approximated as u/s, will become approximatively linear. In this extreme case, the diffraction cannot be balanced by the nonlinear effect and solitons cannot be formed. This indicates that the moderate saturable parameter can suppress the instability of the dressed solitons.
and the nonlinear term, approximated as u/s, will become approximatively linear. In this extreme case, the diffraction cannot be balanced by the nonlinear effect and solitons cannot be formed. This indicates that the moderate saturable parameter can suppress the instability of the dressed solitons.
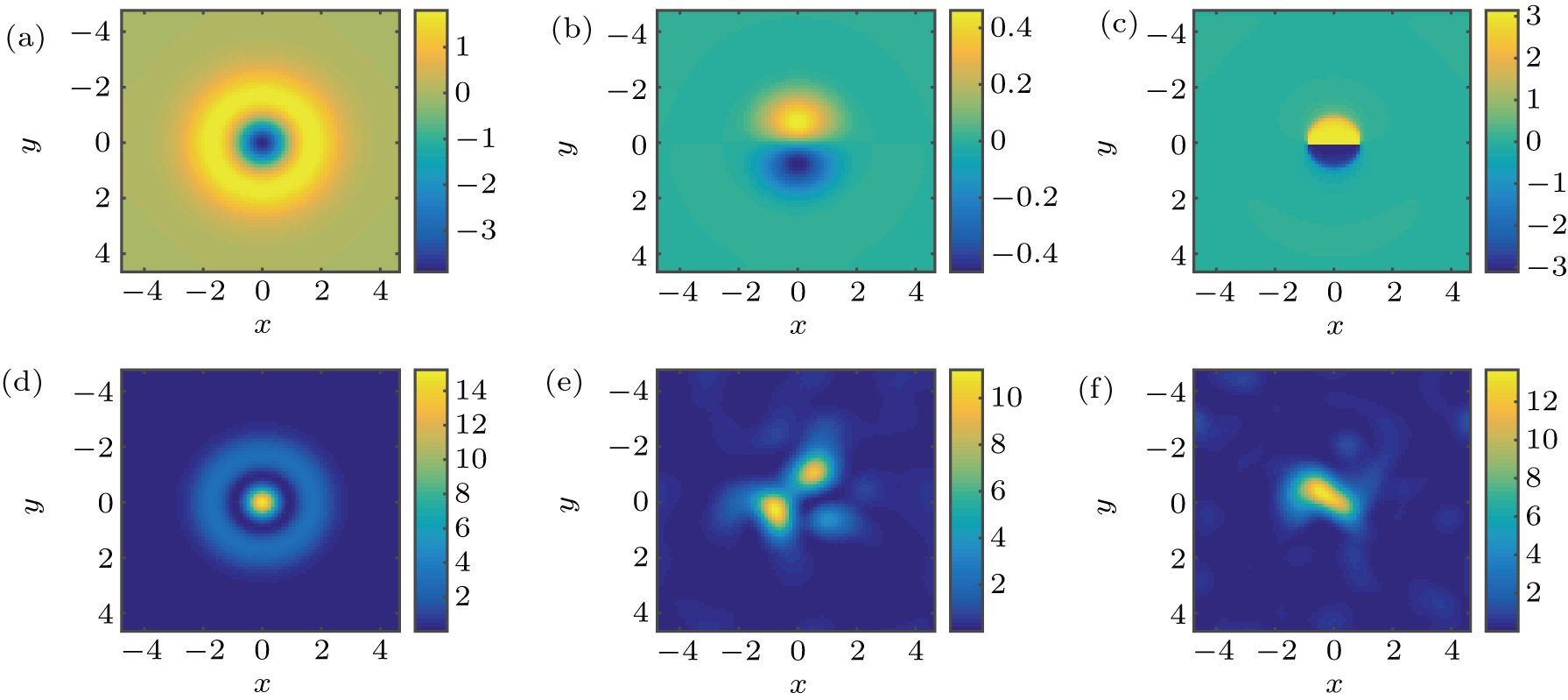
To further demonstrate the propagation stability, we take the dressed soliton at μ =1 and s = 0.5 as a typical stable example. The corresponding propagation stability is shown in Fig. 7. Figure 7(a) and 7(b) show the real and imaginary part of the optical field. Owing to the presence of the PT-symmetric potential, the dressed soliton solution also should be complex. The real part of the optical field is cylindrically symmetric and it has a Gaussian-like profile surrounded by a ring, while the imaginary part is anti-symmetric. Figure 7(c) is the phase structure. It can be seen that the dressed soliton has a uniform phase structure except in the central region where the central intensity hump is seated. To obtain this special phase structure, we can let an optical beam pass through a computer-generated-hologram based phase mask or a two-dimensional spatial light modulator. After passing through the phase element, the beams can carry this special phase structure to excite dressed solitons in the experiment. Figure 7(d) shows the intensity profiles of the stable dressed soliton at the input face. The dressed soliton has an intensity hump in the center, surrounded by an intensity ring whose intensity is weaker than that in the center. From Fig. 6(b), the dressed soliton is completely stable when μ =1 and s = 0.5 because the real part of the instability growth rate is zero. It is also validated by the direct numerical simulations. From Figs. 7(e) and 7(f), respectively, the dressed soliton can keep its intensity profile at z = 50 and z = 100.
To give an unstable example, we plot Fig. 8 to show the optical field and intensity profiles of a dressed soliton when μ = 1 and s = 0.2. From the profiles of optical field, phase, and intensities shown in Figs. 8(a)–8(d), this dressed soliton has a similar profile to those at μ =1 and s = 0.5. Its intensity profile also looks like a hump surrounded by a ring. In this case, the real part of the instability growth rate is 0.823 [shown in Fig. 6(b)], and therefore the dressed soliton is unstable. To validate this conclusion, we do direct simulations of optical propagation after 1% random noises have been added to the numerical solution. From Fig. 6(e), it can be seen that the soliton cannot keep its intensity shape after propagating a distance of 50 units. At z = 100, most of the energy is accumulated in the center, and there is some energy distributed in the background [shown in Fig. 6(f)].
4. ConclusionsIn this work, a theoretical investigation is presented on the existence and propagation stability of optical solitons in nonlinear saturable medium with PT-symmetric Bessel potential. Besides fundamental solitons, a novel type of soliton, namely dressed annunal soliton, is studied in detail. It is found that fundamental solitons exist when μ is above the critical value. All the fundamental solitons are stable. For dressed solitons, there is an intensity hump in the center, which is surrounded by an intensity ring. All the dressed solitons are unstable when s = 0 and 0.2, but dressed solitons with high powers can be stable at high s values, which is completely different from the multi-peak solitons in Kerr nonlinearity with periodical potentials. The higher the staturable parameter s, the higher the normalized power of the dressed soliton is. Furthermore, the moderate saturable parameter (e.g., s = 0.5) can help stabilize the dressed solitons effectively.