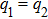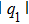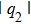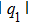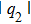† Corresponding author. E-mail:
By means of the modified Darboux transformation we obtain some types of rogue waves in two-coupled nonlinear Schrödinger equations. Our results show that the two components admits the symmetry and asymmetry rogue wave solutions, which arises from the joint action of self-phase, cross-phase modulation, and coherent coupling term. We also obtain the analytical transformation from the initial seed solution to unique rogue waves with the bountiful pair structure. In a special case, the asymmetry rogue wave can own the spatial and temporal symmetry gradually, which is controlled by one parameter. It is worth pointing out that the rogue wave of two components can share the temporal inversion symmetry.
The concept of rogue wave (RW) has been introduced in the investigation of oceanography,[1,2] (and references therein), starting with modeling a short-lived large amplitude wave in ocean. Furthermore, the rogue waves have also been studied in many fields, such as photonic crystal fibers,[3,4] space plasmas,[5–7] Bose–Einstein condensate,[8] water tanks,[9–11] and magnetic nanowires[12–14] driven by the external magnetic field or spin-polarized current. However, there is no exact definition for RW. In general, an RW means that the height of a rogue wave is two or more times those of the surrounding waves. The studies of RW in single-component system have indicated that the rational solution of the nonlinear Schrödinger equation can be used to describe this phenomenon well.[15–23] The lowest-order rational solutions[18,19] also can be obtained by Hirota technique for the discrete Ablowitz-Ladik and Hirota equations. Depending on the parameters chosen for the modulational unstable plane wave the lowest-order RW in the Sasa–Satsuma equation can feature a two-hump structure,[24,25] as well as an analog of the Peregrine soliton.[26–31]
However, many real complex systems usually involve more than one component, such as Bose–Einstein condensates, nonlinear optical fibers, and so on. Recently, the first-order rational solutions of a coupled nonlinear Schrödinger (CNLS) and Maxwell–Bloch equations have been reported in Refs. [32–36]. Some unique properties are obtained for the multicomponent system.[32,37–39] Dark RWs have been presented numerically.[39] and analytically.[40] Moreover, the emergence of two RWs[38,41,42] in the coupled-component system is quite distinct from the high-order RW in one-component system.[40,43,44] The interaction between RW and other nonlinear waves of the two-component coupled systems is also a hot topic of great interest.[37,38,40] Nonlinearly coupled dynamic systems with two or more degrees of freedom have attracted considerable interest for many years.[45,46] The localized waves and all kinds of soliton and soliton–soliton interaction solutions[42,47,48] have been observed in CNLS equation. It is well known that the CNLS equations has a wide range of physical backgrounds. It is a general equation describing wave propagation in weakly nonlinear media, widely used in plasma physics and nonlinear optics, condensed matter physics, biophysics, and other fields.[49–51] Therefore, the exploration of exact solutions in CNLS equations is an interesting subject both in mathematics and physics.
In this paper, we investigate some types of exact rogue wave solutions in the CNLS equations in terms of the developed Darboux transformation. As an example, we obtain the exact symmetry and asymmetry rogue waves. From these results we also find the two components share the temporal inversion symmetry owing to the joint action of self-phase and cross-phase modulation, as well as the coherent coupling term.
The CNLS equations with negative coherent coupling can describe the propagation of the orthogonally polarized optical waves in an isotropic medium. In the paraxial approximation the CNLS equations takes the form[52,53]
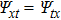
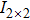
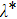
In this paper, we adopt the Darboux transformation method and mainly investigate the symmetry and asymmetric rogue waves. To this purpose we choose the initial seed solutions of Eq. (
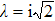
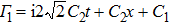

It is interesting to point out that the difference of the self-phase modulation and cross-phase modulation, and the coherent coupling term in Eq. (
Firstly, we consider the case 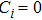
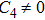
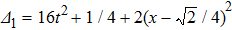
The solution in Eq. (
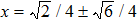
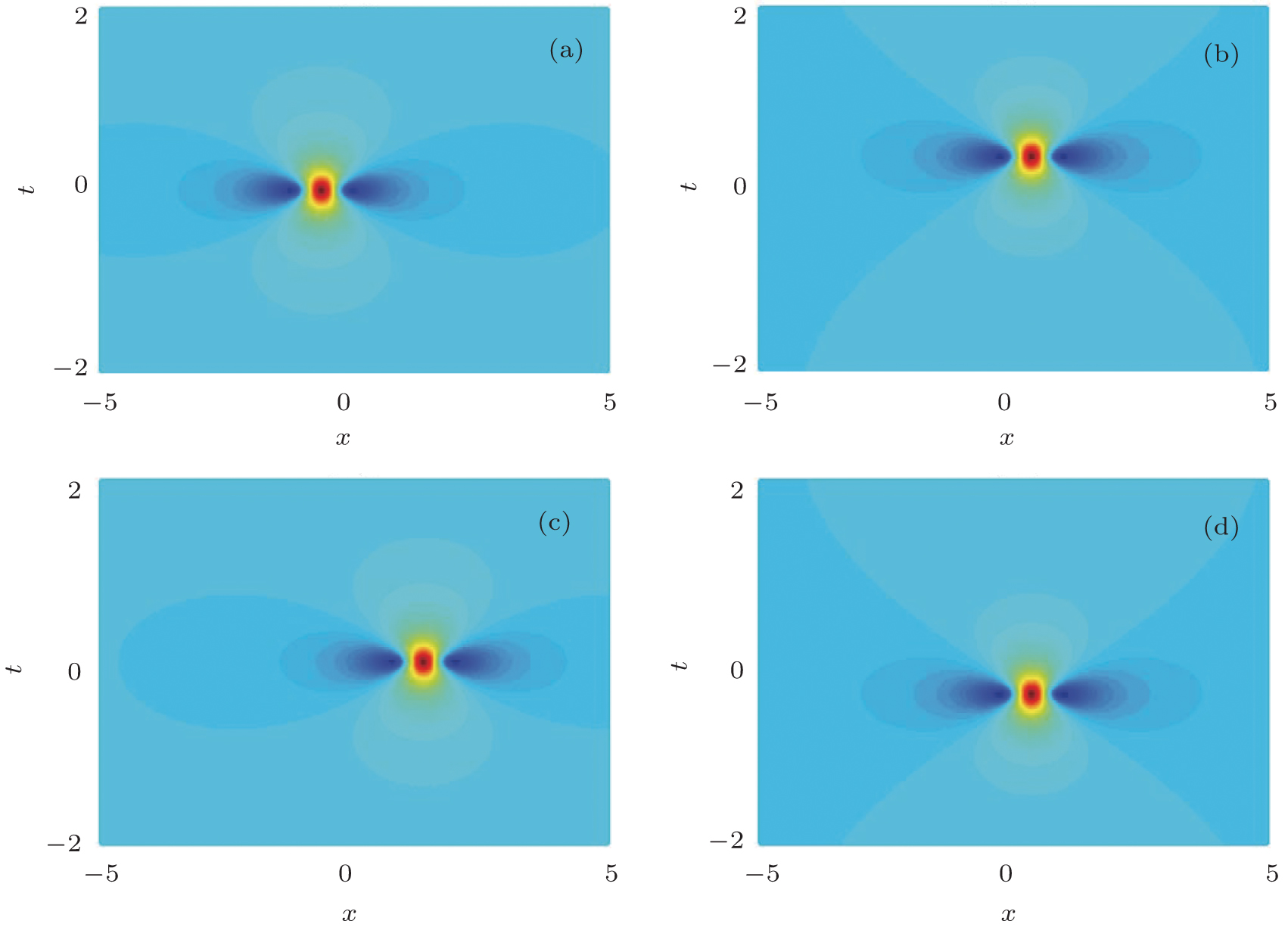
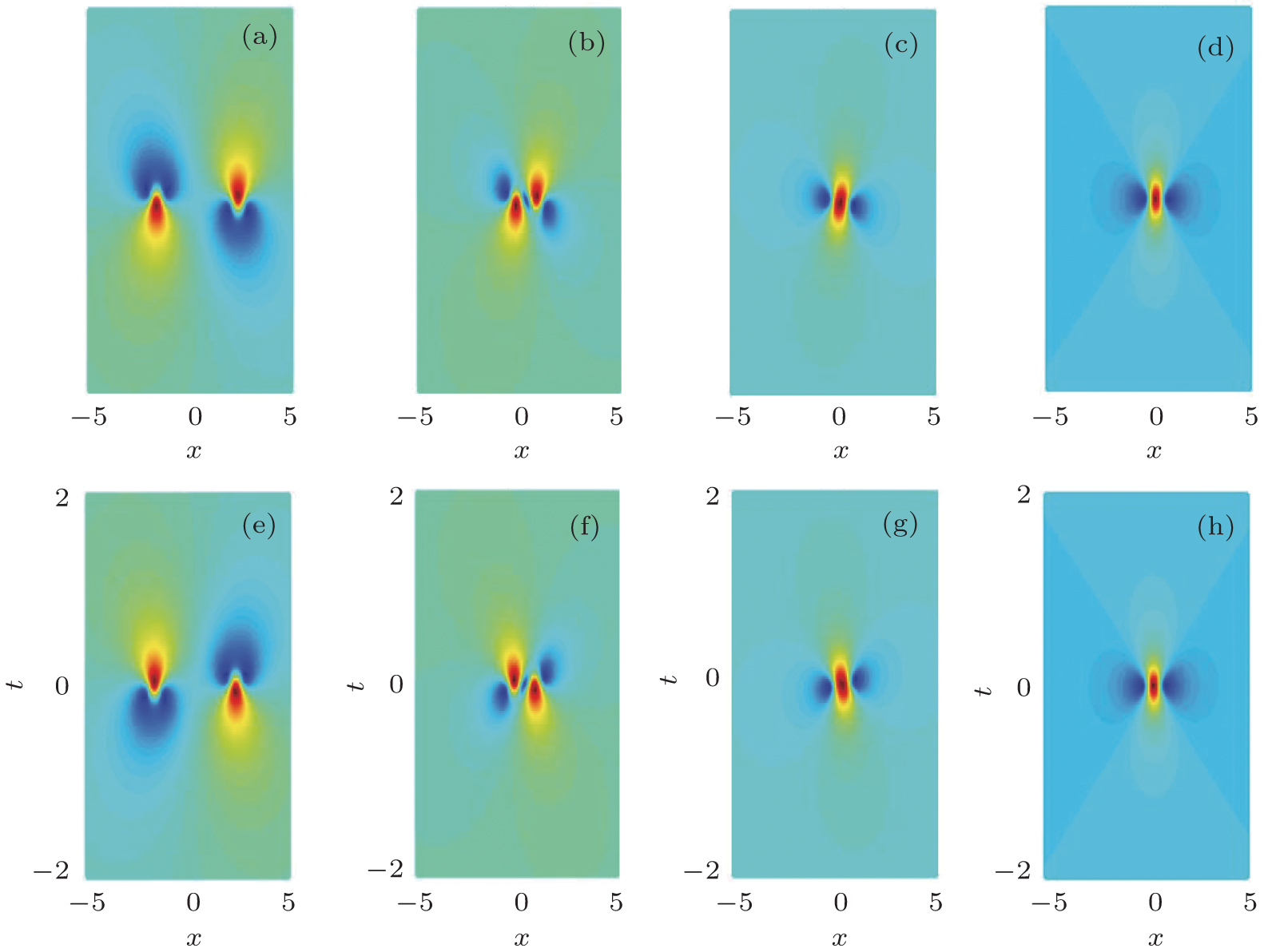
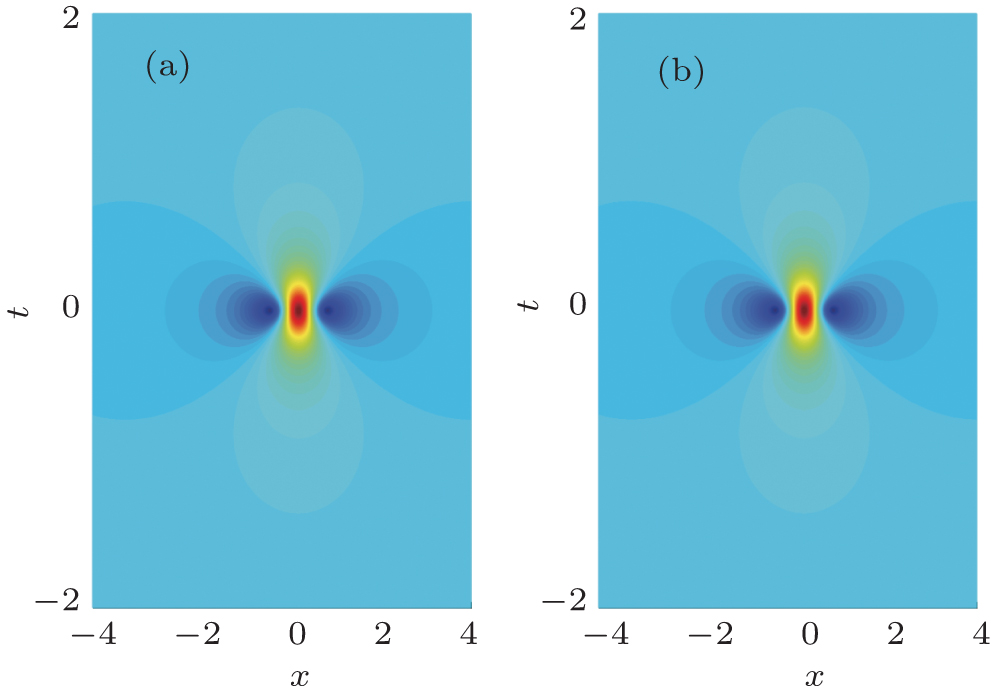 | Fig. 1. (color online) The illustration of vector rogue wave envelope distribution for two component: (a) 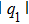
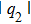
|
Secondly, we consider the case 
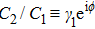
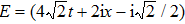
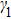
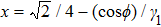
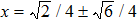
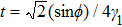
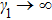
The very interesting phenomenon is that equation (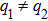

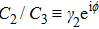
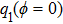
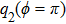
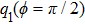
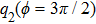
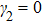
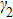
In order to discuss the detail illustration of rogue wave solutions in Eq. (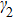
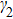
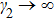
Secondly, we consider the case ϕ = π/2. Similar the above discussion the rogue wave solution in Eq. (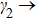
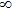
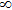

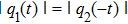
In this paper, in terms of the developed the Darboux transformation we give some types of exact rogue wave solutions in the CNLS equations, which can be used to describe transition dynamics of a one-dimensional or two-component Bose–Einstein condensate system with particle transition in strong interaction regimes and other nonlinear systems. Under the affection of coherent coupling terms, the CNLS equations admits the symmetry and asymmetry rogue waves. We also give the different pair structure of rogue wave which can be adjusted by one parameter. In the special case, we find that the rogue wave solution q1 and q2 can share the temporal inversion symmetry.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] |