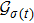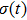† Corresponding author. E-mail:
This paper investigates the time-varying formation problem for general linear multi-agent systems using distributed event-triggered control strategy. Different from the previous works, to achieve the desired time-varying formation, a distributed control scheme is designed in an event-triggered way, in which for each agent the controller is triggered only at its own event times. The interaction topology among agents is assumed to be switching. The common Lyapunov function as well as Riccati inequality is applied to solve the time-varying formation problem. Moreover, the Zeno behavior of triggering time sequences can be excluded for each agent. Finally, a simulation example is presented to illustrate the effectiveness of the theoretical results.
In recent years, the research on formation control of multi-agent systems has received significant attention from both scientific and engineering communities, which has great potential applications in broad areas such as load transportation,[1] static and dynamic obstacle avoidance,[2] and unmanned aerial vehicles formation.[3–5]
Formation control is a significant issue in cooperative control for multi-agent systems. A formation is defined as a predetermined special configuration (such as desired positions or orientations) formed by a cluster of interconnected agents, in which a global goal is achieved cooperatively.[6] Generally speaking, formation can be divided into fixed formation and time-varying formation. Most existing results considered fixed formation control, for example in Refs. [7] and [8] and the literature therein, to name a few. However, in many real applications, the environment may often change and the target is always moving. This motivates several researches on time-varying formation.[9–11] In addition, the derivative of time-varying formation vector may help to analyze and design the formation control strategy, which is the main difference between fixed formation control and time-varying formation control. Thus it is more utility to study time-varying formation control problem. It is worth mentioning that not all time-varying formation can be directly achieved. Hence a description of the feasible constraints (called the feasibility conditions) for time-varying formation control is usually given.[11–13]
Recently, the consensus problem for multi-agent systems has been greatly studied.[14–20] It is found that consensus method can be used to deal with formation control problem. The consensus-based method for formation problem has been developed in such as Refs. [12,13,21–24]. In Ref. [12], the distributed adaptive time-varying formation control problem for multi-agent systems with fixed topology was introduced. Other relevant researches on formation control under fixed topology can be found in Refs. [22–24]. Considering the fact that the interaction topology among agents may change dynamically, formation control for multi-agent systems under switching topologies was addressed in Refs. [11,13], and [21]. Compared with Refs. [13] and [21], the feasibility condition in Ref. [11] is easier to test and the complexity of the proof is reduced.
In most existing formation control strategies, controller always updates continuously. However, such control strategies might be inefficient or impractical in multi-agent systems since they can lead to large communication load and waste excessive resources. Recently, researchers exhibit novel interests on event-triggered control since it is beneficial to coordination of multi-agent systems and can facilitate the efficient usage of the shared resources. In event-triggered control, data transmission or controller actuation times are determined by an event-triggering mechanism. The event-triggered control often depends on a well-defined event-triggering condition in which the measurement error plays an essential role. Many works on event-triggered control for multi-agent systems focused on the consensus problem.[25–28] In Refs. [25–27], the consensus can be achieved asymptotically via event-triggered control under fixed topology. The consensus problem under switching topologies with event-triggered strategy was studied in Ref. [28]. The event-triggering containment control of multi-agent networks with fixed and switching topologies was investigated in Ref. [29]. In practice, communication delays are inevitable. In Ref. [30], event-triggered tracking control of leader-follower multi-agent systems with communication delays was discussed. However, to our best knowledge, there are few results on time-varying formation problem for multi-agent systems via event-triggered control . This motivates our study.
Motivated by the above considerations, in this paper, we aim at dealing with the time-varying formation problem of multi-agent systems with general linear dynamics via distributed event-triggered control under switching topologies. The contributions of our work are four-fold: (i) The formation is time-varying, which has better flexibility. A feasibility condition for time-varying formation is given. In Ref. [31], the formation is assumed to be fixed. The results for time-invariant formation cannot be directly applied to time-varying formation. And in Ref. [21], the feasibility condition is more difficult to test than ours. (ii) A distributed event-triggered control scheme is designed. For each agent, the controller is triggered only at its own event times. In Refs. [12,13,21–24], their controllers are updated continuously, which may lead to large communication load and waste excessive resources. (iii) The interaction topology among agents is switching, which is more practical and challenging than fixed topology. In this case, the formation problem of the multi-agent system is changed into a stabilization problem of a switched system. A common Lyapunov function method is applied, which is more concise than the multiple Lyapunov functions method in Ref. [21]. (iv) It is further shown that the Zeno behavior can be avoided in the distributed event-triggered scheme, which means that two inter-execution instants have a positive lower bound.
The rest of this paper is organized as follows. In Section
An undirected graph 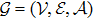
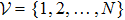
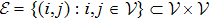
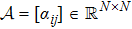
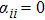
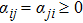
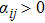
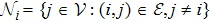
Define the Laplacian matrix L with respect to graph 
 |

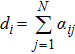
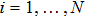
By the definition, for undirected graph, L is symmetric and every row sum of it is zero. Zero 0 is an eigenvalue of L and 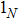
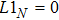
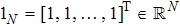
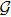
In this paper, the dynamics of each agent is described by
 |
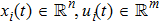
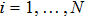
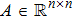
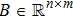
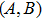
We define that the vector 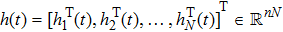
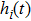
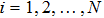
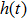
According to the definition of E in Eq. (
In this section, we will consider the time-varying formation problem of multi-agent systems by distributed event-triggered control strategy.
We assume the adjacency graph is undirected and connected and the topology structure between agents is switching. Define the switching signal 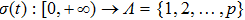
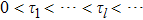
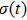
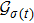
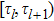
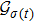
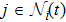

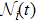
For saving energy, we construct the control law based on event-triggering strategy and assume the triggering mechanism is in the distributed style that the triggering instants are different for each agent. The event-triggering time sequence for agent i is denoted by 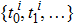
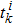
In event-triggered strategy, agents only update their states at the time when some event conditions are triggered. Therefore, when 
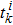
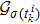
Let 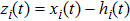
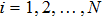
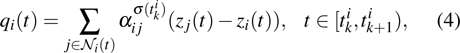 |
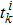
At time 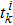
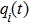

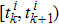

The measurement error can be defined as
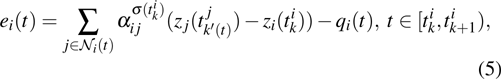 |
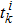
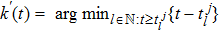
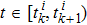
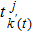
The event-triggering times 
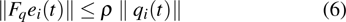 |
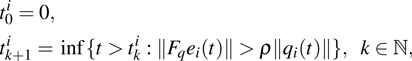 |
Then the distributed control law for agent i is designed as
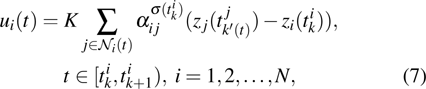 |
In the time interval 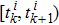
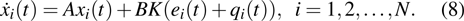 |
Denote
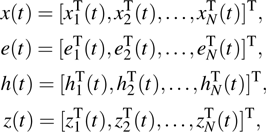 |
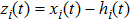
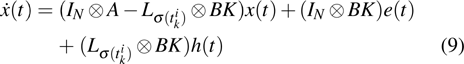 |
 |
Define 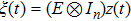
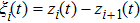
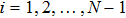
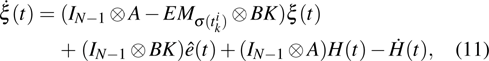 |
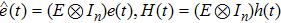

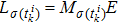
In this section, the feasibility of the proposed event-triggered control strategy will be analyzed by excluding the Zeno behavior. We will prove that in the triggering condition (
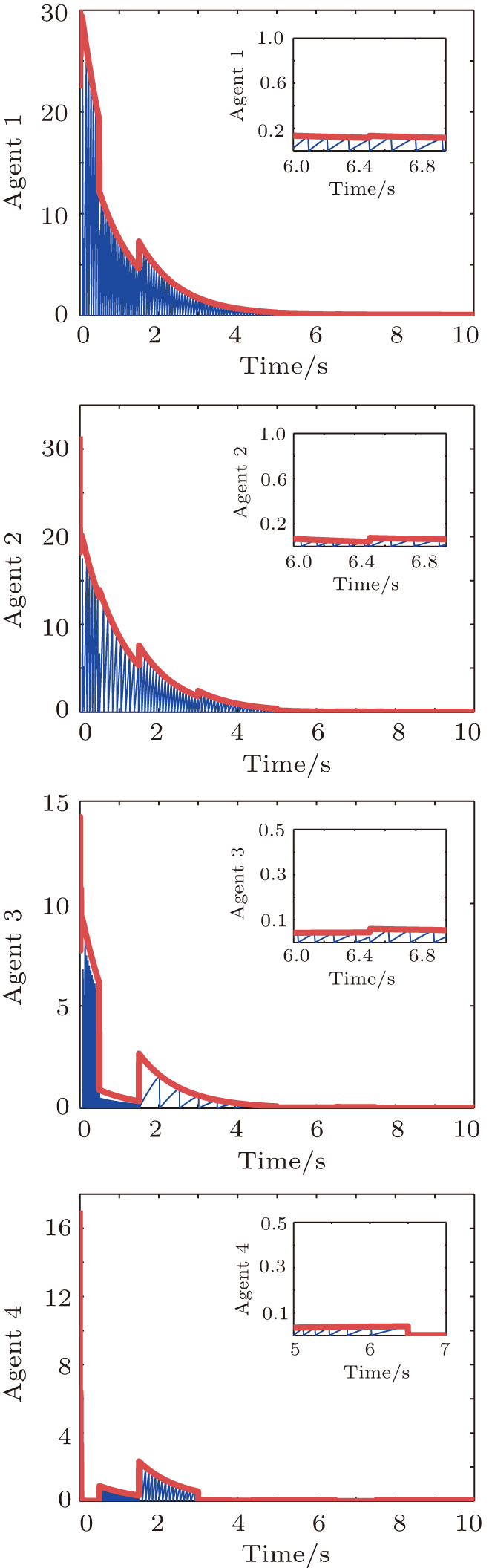
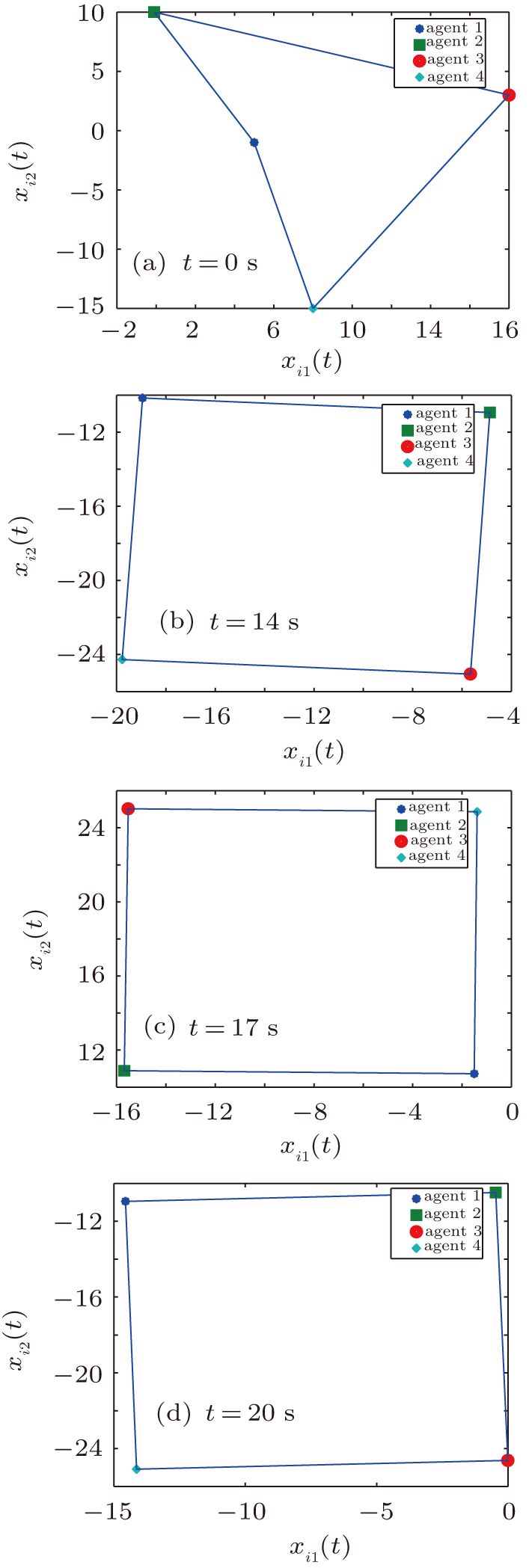
In this section, a numerical example is provided to demonstrate the effectiveness of the results obtained in the previous section. In this example, the multi-agent system consists of four agents satisfying Eq. (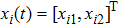
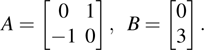 |
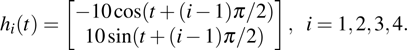 |
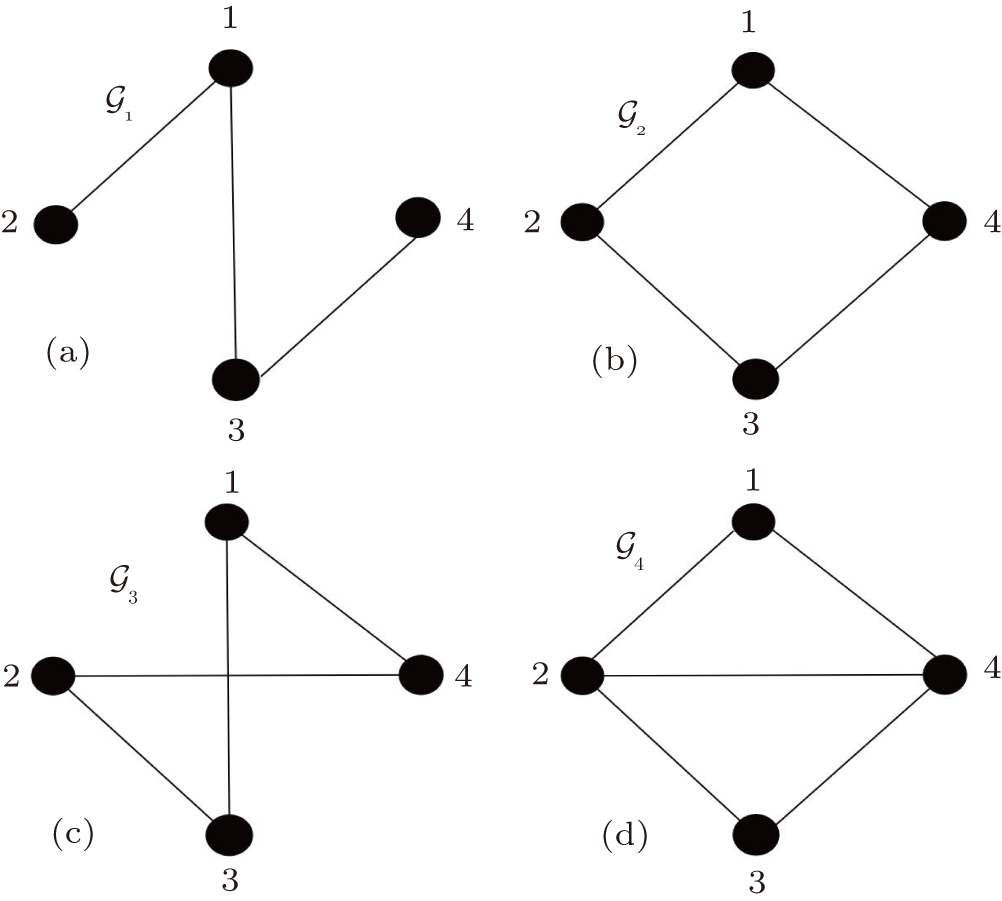
Assume the interaction topology between agents is time-varying. Four possible adjacency graphs, denoted by 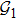

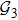


 |
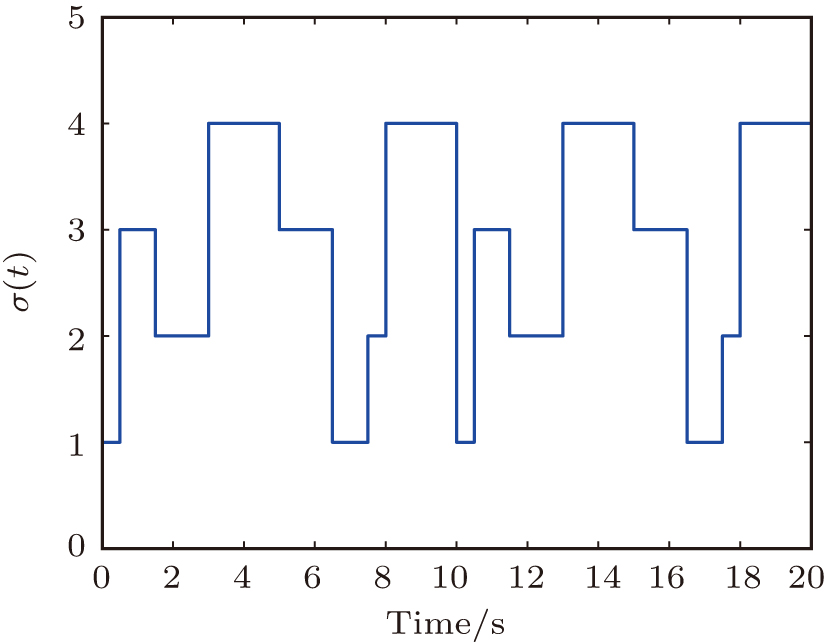
The topology graphs are switched according to 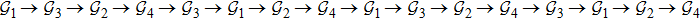
Choose ρ = 1, α = 0.7421, β = 24.7047, ϵ = 2, and 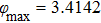
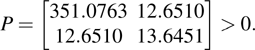 |

With the initial values 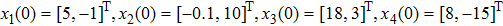
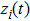
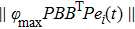
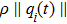

In this paper, the time-varying formation problem for general linear multi-agent systems under switching topologies was studied. A distributed event-triggered control scheme was designed, in which the controller was updated only when the event condition was driven. Using this kind of controller, one can prove that the desired time-varying formation can be reached if the communication graph is switching and connected. We also showed that the Zeno behavior can be avoided in the event-triggered control scheme. A simulation example was given to illustrate the effectiveness of the proposed control law.
Future research will focus on the formation problem of multi-agent systems subject to unknown external disturbances and communication delays via sliding mode control.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] |