† Corresponding author. E-mail:
We show that the freezing phenomenon, exhibited by a specific class of two-qubit state under local nondissipative decoherent evolutions, is a common feature of the relative entropy measure of quantum coherence and correlation. All those measurement outcomes, preserve a constant value in the considered noisy channels, but the condition, property and mechanism of the freezing phenomenon for quantum coherence are different from those of the quantum correlation.
Quantum coherence arising from quantum superposition is a fundamental feature of quantum mechanics. It has been widely used as a resource and root concept in quantum information processing,[1] quantum metrology,[2–5] entanglement creation,[6,7] thermodynamics,[8–12] and quantum biology.[13–16] Recently, a rigorous theory of coherence as a physical resource has been developed.[17–19] Within such a physical resource frame of coherence, some coherence measures have been proposed and investigated, such as the l1 norm of coherence and the relative entropy of coherence.[17]
Quantum coherence in a multipartite system involves the essence of quantum correlations. One of the potential quantum correlations is quantum discord, which may even exist in a separable state with vanished entanglement.[20–24] Quantum discord also is a crucial resource for the development of quantum technologies, such as quantum communication,[25,26] quantum computation,[27,28] etc.
Quantum coherence and discord are both useful physical resources, but the quantum coherence and discord of a quantum state are often destroyed by the noise of the environment. A challenge in exploiting these resources is to protect them from decoherence caused by noise. One of the most fascinating phenomena observed in the dynamics of quantum coherence and discord is the possibility for its freezing, that is, complete time invariance without any external control, in the presence of particular initial states and noisy evolutions. In fact numerous studies have focused on the freezing phenomenon for quantum discord and coherence. Under the local non-dissipative decoherence evolution, it has been observed that a number of known discord-type measures all remain constant for a finite time interval in Markovian conditions[29–33] and for multiple intervals,[34–36] or forever[37] in non-Markovian conditions, when considering two non-interacting qubits initially in a specific class of Bell-diagonal (BD) states. Recently, the quantum coherence can also remain frozen under local nondissipative decoherence channels, for the particular initial BD states have been studied.[38–41]
These freezing phenomena are quite appealing since it implies that every protocol relying on discord or coherence as a resource will run with a performance unaffected by noise in the specific dynamical conditions. Currently, these investigations only prove the occurrence of freezing under some particular condition by considering the specific decoherence channel. However, it is natural to ask what properties these freezing phenomena have and why these freezing phenomena can occur. This work addresses such issues. Furthermore, we know that the quantum coherence and correlations have intimate relations between them. Many efforts have been devoted to the investigation of the connections between quantum coherence and quantum correlations in multipartite systems,[42–46] Through comparative investigation of the freezing phenomena for quantum coherence and discord we can better understand the relations between them.
As is well known, the different measures of quantum resource are not identical and conceptually different. Different quantum resources do not coincide with each other for different measures, and a direct comparison of two notions is rather meaningless. So we only focus on the measures based on the relative entropy, which enjoys the properties of physical interpretation and being easily computed.
The rest of the paper is organized as follows. In section
The relative entropy between two quantum states ρ and σ is defined as
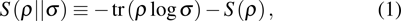 |

Given any quantum state ρ, one can list the relative entropy of discord D and the relative entropy of coherence C as follows:
 |
 |

 |
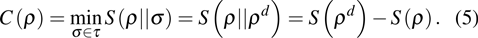 |
The BD states are structurally simple states which nonetheless remain of high relevance to theoretical and experimental research in quantum information, as they include the well-known Bell and Werner states.[47] Usually, the BD states have two forms. The first form of the BD states is described by diagonal elements in the basis of the four maximally entangled Bell states, that is,
 |




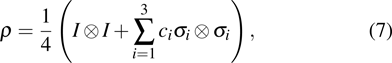 |

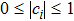

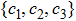
As is well known, for any quantum state ρ, the closest incoherent state 

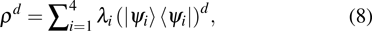 |
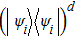
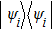
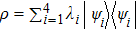


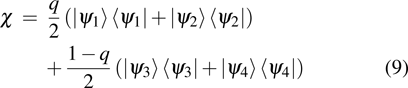 |

We consider paradigmatic instances of incoherent channels which embody typical noise sources in quantum information processing.[1] The bit flip, bit-phase flip, and phase flip channels which are represented in Kraus form by 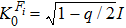
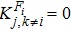


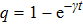





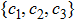
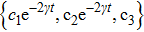
Bromley et al. studied the conditions for frozen quantum coherence in Ref. [38]. They first showed the properties of the evolution of a quantum system under particular noisy channels, and then proved that all bona fide distance-based coherence monotones are left invariant during the entire evolution under certain conditions of the initial states. Conversely, in this section, we first show that the relative entropy of coherence is determined only by one element of the BD states with 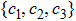
For convenience, in the following, we define the density operators 

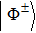

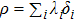


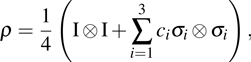 |
 |
According to formulas (
 |
If 
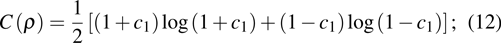 |
If 
 |
As we know, local bit flip channels on each qubit map initial BD states with 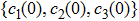

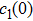
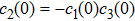


 |
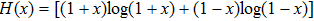


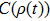

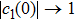

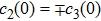
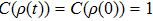
 |
 |

 |
Considering the definition of the l1 norm of quantum coherence 
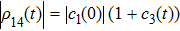



We know that local bit-phase flip channels on each qubit map initial BD states with 
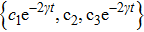
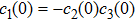

However, from formula (
Cianciaruso et al. have studied the conditions for frozen quantum discord in [32]. They first showed the properties of the evolution of a quantum system interacting with a non-dissipative decohering environment, and then proved that the quantum discord measured by geometric approach remains constant during the evolution for a paradigmatic class of two-qubit state. In this section, we first show that the relative entropy of discord is determined only by one element of the BD states with 
For calculating the relative entropy of discord, we list the ordering for all 


 |
Considering that the condition 

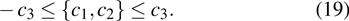 |


 |

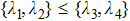

 |

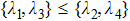

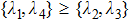
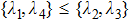

According to formula (
If 

 |
If 

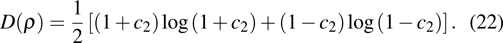 |
If 

 |
If 

 |
If 

 |
If 

 |
As the local bit flip channels on each qubit map initial BD states with 

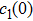





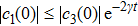


 |

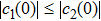

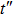
 |
Therefore, we can obtain two conditions for freezing the quantum discord when the quantum systems undergo local identical bit flip channels. The first condition is the initial BD states with 

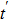



 |
We know that 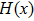



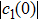


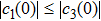

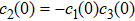



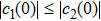

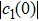
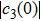

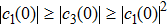
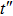
 |


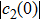

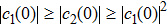
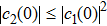
We now show why the frozen quantum discord can occur and why the freezing phenomenon is present in a finite time. For the initial BD states with 
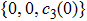
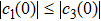
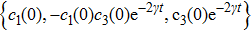


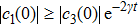
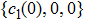
 |
 |
 |
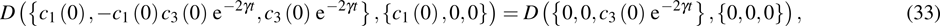 |
For the initial BD states with 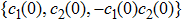

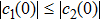

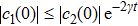



Similarly, as local bit phase flip channels on each qubit map initial BD states with 

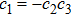



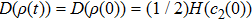


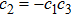




In this paper, in terms of the definitions of the relative entropy of coherence and discord, we have derived the conditions for freezing phenomenon when the quantum systems undergo bit flip, bit-phase flip, and phase flip channels, respectively. We find that the freezing phenomenon for quantum coherence can occur only in bit flip and bit-phase flip channels, but the freezing phenomenon for quantum discord can be present in bit flip, bit phase flip, and phase flip channels. The conditions for freezing the discord are stricter than for freezing the coherence, but the discord can be frozen via two conditions. We have investigated the properties of the frozen quantum coherence and frozen quantum discord. We find that the quantum coherence is frozen forever under certain conditions, but the freezing phenomenon for quantum discord is present within a finite time under some conditions. Furthermore, the frozen quantum coherence can reach its maximal value, but the frozen quantum discord cannot reach its maximal value, and the threshold time decreases with the increase of the value of frozen quantum discord. We show that the reasons for freezing the quantum coherence are the coherence interchange in the quantum systems, and the freezing of quantum discord is caused by the properties of the measurement which are used to measure quantum discord.
From a fundamental perspective it is important to understand in depth the physical origin of frozen quantum coherence and the relation between quantum coherence and quantum discord. Here, we identify all the conditions for the freezing phenomenon in the mathematically rigorous form, and a comparison among these conditions can help us better understand the freezing phenomenon and the relations between quantum coherence and quantum discord. The reasons for the freezing phenomenon, we provide here, may describe the essence of the freezing phenomenon for quantum coherence and discord, so this work may provide some clues to its further investigation. Recently, the connection between quantum coherence and discord has been established in Ref. [48], through our work we can see the difference between the quantum coherence and discord.
Our result also has an influence from an applicative point of view: the property immune from the noise makes quantum coherence and quantum correlations important for the realisation of quantum technologies. Further research on this question can lead to a more efficient exploitation of coherence and discord for empowering the performance of real-world quantum technologies to be applied to communication, computation, sensing, and metrology.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] |

