† Corresponding author. E-mail:
This paper is concerned with the generalized variable-coefficient nonlinear evolution equation (vc-NLEE). The complete integrability classification is presented, and the integrable conditions for the generalized variable-coefficient equations are obtained by the Painlevé analysis. Then, the exact explicit solutions to these vc-NLEEs are investigated by the truncated expansion method, and the Lax pairs (LP) of the vc-NLEEs are constructed in terms of the integrable conditions.
The Painlevé test could to provide useful information for the identification of completely integrable PDEs, which are of importance in nonlinear theory and physical applications. In addition, they also appear to yield other integrable properties such as Lax pairs (LPs), Bäcklund transformations (BTs), rational solutions, and so on (see e.g., Refs. [1–3] and the references therein).
On the other hand, to find exact solutions to the nonlinear evolution equations (NLEEs) is always one of the themes in mathematics and physics. In the past few decades, there are noticeable progresses in this field, and various methods have been developed, such as the inverse scattering method,[4,5] Darboux and Bäcklund transformations,[6–8] Lie symmetry analysis,[9–13] dynamical system method,[14,15] trial function method (direct method),[11,16] Painlevé test,[1–3,12,17–19] and so on. In the present paper, we consider the generalized variable-coefficient nonlinear evolution equation (vc-NLEE) as follows:
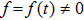
This equation is also called the variable-coefficient generalized Burgers–KdV type equation sometimes. Such vc-NLEE plays a significant role in mathematical physics, integrable system, and physical applications, etc.[17,18] However, to obtain the exact solutions and integrability of the variable-coefficient equation in generalized form are more involved. By the equivalent transformation, the variable-coefficient equation can be transformed into constant-coefficient equation under some conditions, so the exact solutions are obtained accordingly.[20] This is a useful method for dealing with exact solutions to the vc-NLEEs, but the integrability of the vc-NLEE may be different from the constant-coefficient equation. In Ref. [12], the Painlevé test and Lie group analysis are performed for the variable-coefficient nonlinear evolution equations (including the cylindrical KdV type equations), but the equation is not the generalized form and it differs greatly from Eq. (
The main purpose of this paper is to investigate the complete integrability classification of the generalized vc-BKdV equation by Painlevé test. The remainder of this paper is organized as follows. In Section
In this section, we employ the Kruskal’s simplified method[1–3] to carry out the Painlevé test for Eq. (
First of all, we assume that
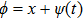
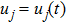
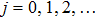
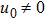
Then, by using the leading order analysis, we obtain the following results:
(i) 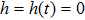
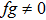
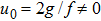
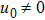
(ii) 
When p = 1, we have ρ = 2 and 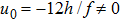
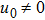
When p = 2, we have 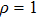
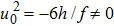
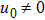
Summarizing the above discussion, we obtain a necessary condition of integrability as follows:
In what follows, under the integrable conditions, we perform the Painlevé analysis completely, so the Painlevé integrability classification of Eq. (
In this case, equation (
Thus, substituting Eq. (
By using Eqs. (
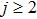
In view of Eq. (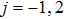
Thus, let 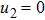
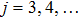
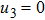

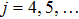
So, we can say that equation (
Thus, we have the following result.
Furthermore, the complete classification in terms of Eq. (
Summarizing the above discussion, we have
To sum up, we have
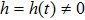
From Eq. (
Summarizing the above discussions, we achieve the following result.
Summarizing the above argument, we achieve the following result.
In this paper, the complete integrability classification of the generalized variable-coefficient nonlinear evolution equation is investigated by the Painlevé analysis method. The integrable conditions for the vc-NLEEs are obtained in the sense of simplified Painlevé test, and the exact explicit solutions are obtained by the truncated expansion method. Then the Lax pairs of the equations are given under the integrable conditions. Moreover, for the integrable equations, the other properties, such as Bäcklund transformations, infinite generalized symmetries, and conservation laws (CLs) can be considered through other methods, the details are omitted in this paper.
Remark 1 In fact, the Painlevé analysis is a powerful method for dealing with intrinsic properties and exact solutions to the nonlinear equations. But the simplified Painlevé test differs from the general Painlevé test[1–3,19] for dealing with integrable properties and exact solutions sometimes.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] |

