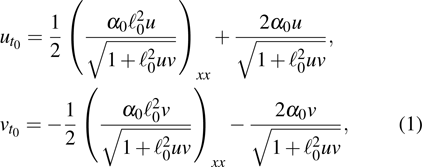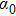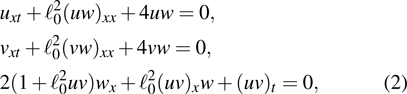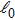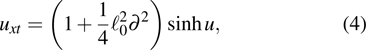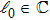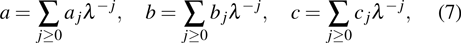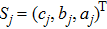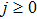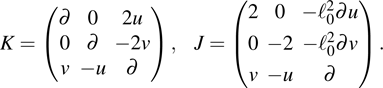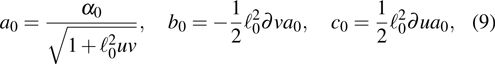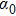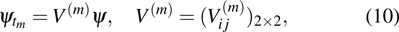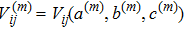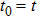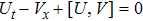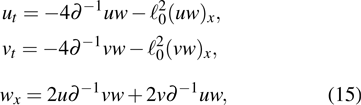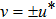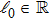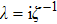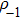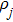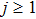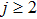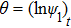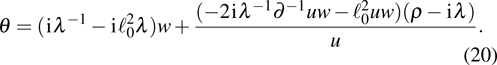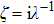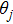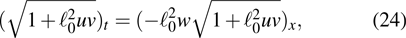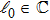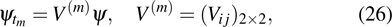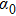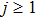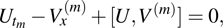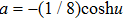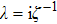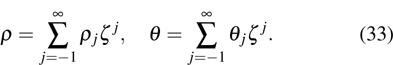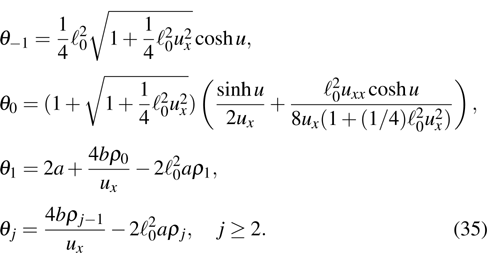An extension of integrable equations related to AKNS and WKI spectral problems and their reductions
1. IntroductionA most active field of recent research involved in applied mathematics and theoretical physics is concerned with integrable systems.[1–6] The AKNS system is an important integrable model for leading to a wide class of nonlinear evolution equations such as the KdV, the nonlinear Schrödinger, the mKdV, the sine-Gordon equations, and others.[7] The WKI model, proposed in Ref. [8], could describe the nonlinear oscillation of elastic beams under tension. Various methods have been developed to study integrable systems, for instance, the inverse scattering transformation,[9–11] the Darboux and Bäcklund transformation,[12–14] the algebraic-geometrical approach,[15–17] and others.[18–20] It is discovered that two inverse scattering formalisms of the AKNS and WKI models are connected through a generalized gauge transformation and a transformation of the space and time coordinates depending on a dependent variable.[21]
The main aim of this article is to study the extension of integrable nonlinear evolution equations related to the combined AKNS and WKI spectral problems and their reductions. In section 2, with the aid of the zero-curvature equation, we obtain a novel hierarchy of integrable nonlinear evolution equations associated with a 2 × 2 matrix spectral problem. The first nontrivial member is
where
u and
v are two potentials,
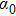
and

are constants. A key feature of Eq. (
1) is that the nonlinear term appears in the form of

, which implies that the system is highly nonlinear. Then we deduce a negative flow associated with the same 2 × 2 matrix spectral problem
in which
u,
v, and
w are three potentials,
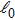
is a constant. We obtain the infinite many conservation laws of Eq. (
2) with the aid of the Riccati forms for the two linear spectral problems. In section
3, we discuss the reduction of the hierarchy in section
2 and obtain a novel hierarchy of nonlinear evolution equations, in which the first member is
where
u is a potential,

and

are constants. Based on a deep reduction of the negative flow, we deduce a novel integrable generalization of the sinh-Gordon equation
which can be reduced to the classical sinh-Gordon equation for

. We similarly obtain the Lax pair of Eq. (
4) and derive its infinite many conservation laws.
2. Extension related to the AKNS and WKI spectral problemsIn this section, we shall investigate the following 2 × 2 matrix spectral problem
where
u and
v are two potentials,
λ is a constant spectral parameter and
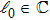
is a constant parameter. For

spectral problem (
5), which can yield a wide class of nonlinear evolution equations, is just the well-known AKNS spectral problem presented by Ablowitz, Kaup, Newell, and Segur. In order to derive a hierarchy of nonlinear evolution equations associated with spectral problem (
5), we solve the stationary zero-curvature equation
where
and coefficients
aj,
bj,
cj are functions to be determined. A direct calculation shows that equations (
6) and (
7) imply the Lenard recursion equation
with
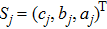
,
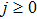
, and the two operators
K,
J defined as
It is easy to calculate that
where
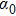
is an arbitrary constant. The recursion relation (
8) can uniquely determine
Sj,

, if the constants of integration are identified as zero.
Case 1 Let ψ satisfy the spectral problem (5) and the auxiliary problem
where each entry
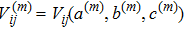
,
Then the compatibility condition of Eqs. (
5) and (
10) yields the zero-curvature equation,

, which is equivalent to a hierarchy of nonlinear evolution equations
The first nontrivial member in the hierarchy is Eq. (
1). Let

,

,
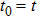
,

or

, then equation (
1) turns to
which is a generalization of the WKI model proposed in Ref. [
8].
Case 2 Assume that ψ satisfies the spectral problem (5) and the following auxiliary problem
where
w is a function to be determined, and

. Here we should point out that the position for the evolution of the space variable and the time variable in the Lax pair, i.e., Eqs. (
5) and (
14), is the same. Therefore, function
w can be regarded also as a potential. The element
Vij of the matrix
V in Eq. (
14) contains an item of
λ with a negative power, which is different to Case 1. The structure of matrix
V ensures that coefficients of
λ with the same power are zero in the zero-curvature equation,
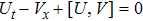
. Meanwhile, the existence of nontrivial nonlinear evolution equations should also be guaranteed. A direct calculation gives rise to a new interesting nonlinear evolution system
which is equivalent to Eq. (
2). Let
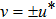
and
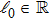
. Then equation (
2) is reduced to a new nonlinear evolution equation
In what follows, we shall derive conservation laws for Eq. (2). Define
 , from the spectral problem (5), we arrive at a Riccati-type equation
, from the spectral problem (5), we arrive at a Riccati-type equation
Let
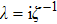
. By inserting the ansatz
into Eq. (
17) and comparing the coefficients of
ζ with the same power, we obtain
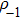
,

, and the recursion formulas for
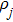
,
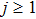
as follows:
for
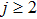
. On the other hand, denote
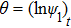
and from the auxiliary problem (
14), we have
Expanding
θ into the following series of
ζ (
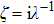
)
we can gain the expressions of
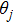
immediately from Eqs. (
18 and (
20)
Since
 , we obtain
, we obtain
The coefficients

and
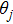
in the expansion of
ρ and
θ are called conservation densities and currents, respectively. Specially, the third expression of Eq. (
2) implies the following conservation law:
which is just the first conservation law in Eq. (
23) for Eq. (
2).
3. Reductions of nonlinear evolution equationsIn this section, we shall discuss a reduction for the hierarchy of nonlinear evolution equations (12). To this end, we shall reconsider the 2 × 2 spectral problem (5) in the case of v = u, i.e.,
where
u is a potential,
λ is a constant spectral parameter, and
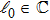
is a constant parameter. The key problem for the reduction is to find the suitable auxiliary problem of Eq. (
25).
Case 1 Let ψ satisfy the spectral problem (25) and the auxiliary problem
where
The coefficients
aj and
bj are determined by the following Lenard recursion equation
with
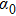
being an arbitrary constant and the two operators
K and
J defined as
If all the constants of integration are identified as zero in the process of recursion calculation by using recursion relation (
27), then the sequence
Sj,
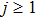
, can be uniquely determined. The compatibility condition of Eqs. (
25) and (
26) yields the zero-curvature equation,
which is equivalent to a hierarchy of nonlinear evolution equations
with

. The first nontrivial member in the hierarchy is Eq. (
3), which is a generalization of the model given in Ref. [
22].
Case 2 Assume that ψ satisfies the spectral problem
and the auxiliary problem
where
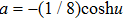
,

. Then the zero-curvature equation,

, generates the novel integrable generalization of the sinh-Gordon equation (
4), which is similar to the generalization of the sine-Gordon equation.
[23] Here the solution
V of the zero-curvature equation in Eq.(
30) can be obtained by assuming that
V is the linear polynomial of
λ and

, and substituting into the zero-curvature equation.
In the following, we shall derive infinitely many conservation laws of Eq. (4) through the same process in section 2. Let
 ,
,
 . From the spectral problem of Eqs. (29) and (30), we obtain the following expressions related to ρ and θ
. From the spectral problem of Eqs. (29) and (30), we obtain the following expressions related to ρ and θ
In Eqs. (31) and (32), functions ρ and θ can be written as a series in powers of ζ (
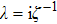 ):
):
Substituting expressions (
33) into Eqs. (
31) and (
32) and comparing powers of
ζ with the same power yield two infinite sequences of conserved quantities for Eq. (
4)
with

, and