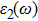† Corresponding author. E-mail:
Comparative analysis of electronic, magnetic, optical, and thermoelectric properties of CdFe2O4, calculated by employing PBEsol + mBJ has been done. The PBEsol reveals metallic nature, while TB-mBJ illustrates ferromagnetic semiconducting behavior. The reasons behind the origin of ferromagnetism are explored by observing the exchange, crystal field, and John–Teller energies. The optical nature is investigated by analyzing dielectric constants, refraction, absorption coefficient, reflectivity, and optical conductivity. Finally, thermoelectric properties are elaborated by describing the electrical and thermal conductivities, Seebeck coefficient, and power factor. The strong absorption for the visible energy and high power factor suggest CdFe2O4 as the potential candidate for renewable energy applications.
The spinel oxides have attracted immense attention of the scientific community, during the past few decades, for their diverse material properties that are suitable for wide range of technological device applications.[1] Among various spinel oxides, CdFe2O4 is considered important due to its normal spinel structure that is composed of Cd+2 and Fe+3 ions located at the tetrahedral and octahedral sites, respectively.[2] The trivalent iron ions form pyrochlore lattice, due to considerable magnetic frustration arising from these antiferromagnetically interacting magnetic ions.[3] The experimental lattice constant of CdFe2O4 spinel oxide is 8.715 Å[4] with the cubic space group 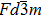
CdFe2O4 has been grown by using a variety of growth techniques for exploring versatile physical properties.[5–9] In a recent experimental report, CdFe2O4 nanoparticles grown by employing a chemical condensation technique revealed a band gap of 1.74 eV, and hysteresis loop was measured at ambient temperature, suggesting potential magnetic and optical device applications,[10] while CdFe2O4 nanoparticles previously prepared by microwave assisted technique had revealed antiferromagnetic nature.[11] Ferrimagnetic ordering in the nanostructured CdFe2O4 spinel with particle size 4–60 nm has been reported to arise due to spin-glass-like surface structure (having huge magnetic anisotropy) that was justified by formation of a mixed spinel exhibiting spin canting at A and B sites.[12] Random distribution of magnetic ions in sputtered thin film of CdFe2O4 spinel has been verified to arise due to annealing. It enhances magnetic properties because of spin-glass-like structure stabilization.[13]
As technologically interesting material properties can be elaborated by theoretical computations, density functional theory (DFT) investigation becomes more relevant as desired conditions can be imposed onto the materials to comprehensively investigate the resulting characteristics. To the best of our knowledge, the DFT studies on CdFe2O4 have been seldom reported. For example, Fe–Fe interactions up to the third neighbor, as investigated by using generalized gradient approximation (GGA) and GGA+U (U is on-site Coulomb interaction), have been reported to operate within the geometrically frustrated cadmium ferrites.[14] Interestingly, third-neighbor interactions were found similar to the first-neighbor interactions.[14] A comparison between Trans-Blaha-modified-Becke-Johnson (TB-mBJ) and GGA+U is applied to investigate optical and magnetic characteristics of CdFe2O4. Both methods generate the consistent material parameters with the experiments.[15] In addition, no report exists in the literature that covers the thermoelectric properties of CdFe2O4.
As there have not been thorough investigations on the physical properties of CdFe2O4, we compare PBEsol functional with TB-mBJ potential by using DFT. The electronic, magnetic, optical, and thermoelectric properties produced by applying PBEsol functional and then mBJ potential are elaborated to demonstrate striking device applications.
In this article, we have used the relaxed structure of cubic spinel oxide CdFe2O4 for strain minimization, and then optimization is done by using FP-LAPW method implemented into Wien2K code.[16] The optimized structure is used for total energy convergence by applying PBEsol[17] functional, and further applying modified Becke and Johnson potential as suggested by Trans and Blaha (TB-mBJ).[18] The selection of PBEsol and TB-mBJ potential is due to the inefficiency of GGA and LDA method in computing the consistent parameters with the experiments.[19,20] The TB-mBJ has quality to improve the electronic structure and band gap that are resonate with the experiments. In TB-mBJ potential, deviations due to GGA and LDA functional are averaged to approach closely to the experimental values. The parameter c (self-consistently converged value) is employed according to
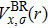
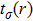
For the self-consistent process, inside and outside the atomic cores, relativistic spherical harmonic type and semi-relativistic approaches are employed respectively. A basis set is employed for controlling the wave function, potential and charge density in the muffin-tin region. The product of muffin-tin sphere radius and the plane-wave cut off in the reciprocal lattice is 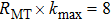

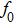
The computations are performed to determine the electronic structures for describing the magnetism in terms of exchange mechanism and John Teller effect. Similarly, optical and various thermoelectric parameters are also computed to reveal energy-related device applications.
The relaxed CdFe2O4 structure has been optimized in ferromagnetic (FM) and antiferromagnetic (AFM) states, and stable FM state is confirmed due to more energy released in FM state than in AFM state. While calculating the AFM, the nearest neighbor layers are flipped in alternative layer to add the spin contribution. The calculated ground state energy in AFM state for all configurations is compared with FM state energy. Stability of FM state is further confirmed due to negative sign of computed enthalpy of formation, as listed in Table 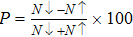
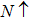
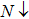
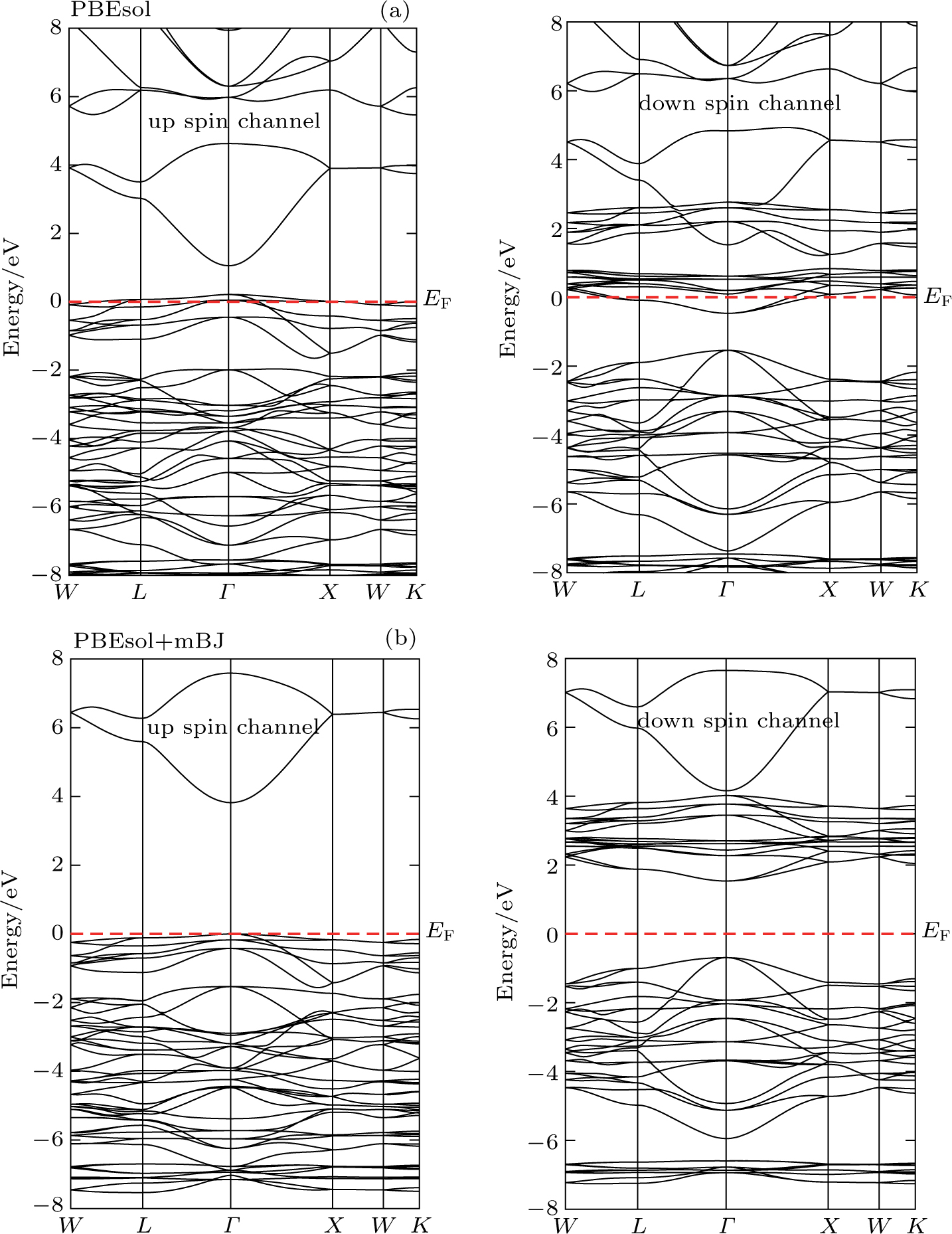 | Fig. 1. (color online) Spin polarized band structures of CdFe2O4 computed by applying PBEsol and PBEsol + mBJ functional. |
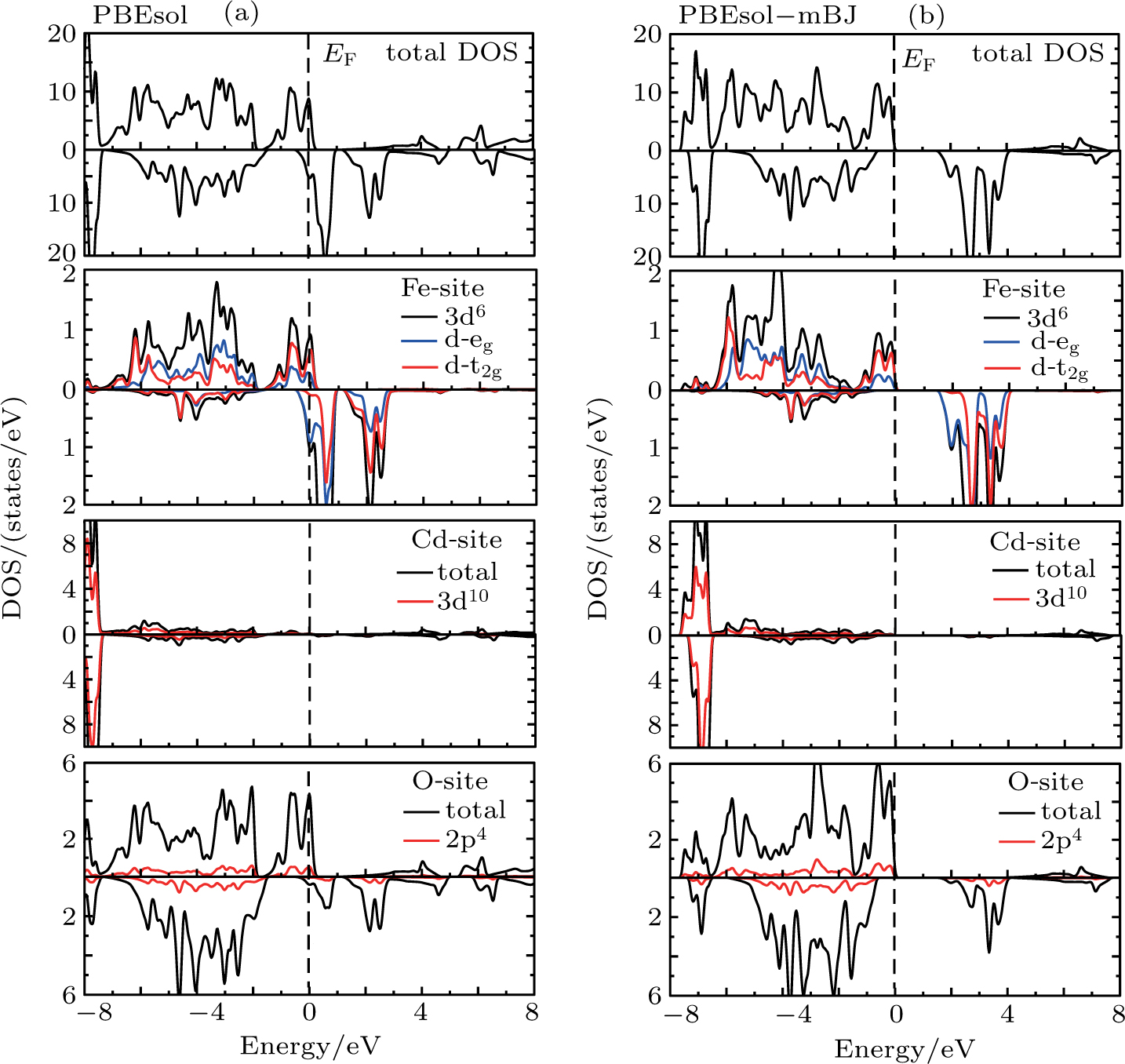 | Fig. 2. (color online) (a), (b) Total (TDOS) and partial density of states (PDOS) determined for CdFe2O4 for both spin configuration by applying PBEsol and PBEsol + mBJ functional. |
| Table 1.
Various parameters calculated for CdFe2O4 in the FM state by using PBEsol and PBEsol + mBJ potentials. . |
The band structures (BS) and density of states (DOS) computed by using TB-mBJ potential, as shown in Figs. 
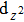
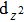
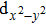
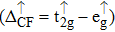
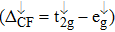
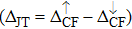
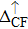

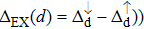
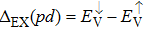

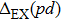
 | Fig. 3. (color online) The splitting of 3d-states of Fe (III) by John Teller distortion (JTE) at octahedral position in the spinel structure of CdFe2O4. |
The magnetic moment with PBEsol functional is an integer while for TB-mBJ potential is a fractional, and that gives the evidence of convergence of metallic to semiconductor. The reduction of magnetic moment of Fe and its sharing to the nonmagnetic sites elucidate the strong hybridization between 3d-states of Fe and 2p-states of O. Computations through TB-mBJ illustrate that shifting of magnetic moment from magnetic to nonmagnetic site is stronger as compared to the computations through PBEsol functional. It suggests that in the studied compound, exchange mechanism is more favored in the ferromagnetic semiconducting than in the metallic compounds. The magnetic moments determined by the varying symmetries such as Fd3m, P3m1, and Pnma are 19.99 μB, 199 μB and 40 μB, respectively. The computed magnetic moment for P3m1 phase is higher, but being the lowest for Fd3m phase, while computed enthalpy of formations shows that CdFe2O4 has the highest stability in Fd3m phase, and this is the reason we have preferred to study the cubic phase of CdFe2O4.[32,33]
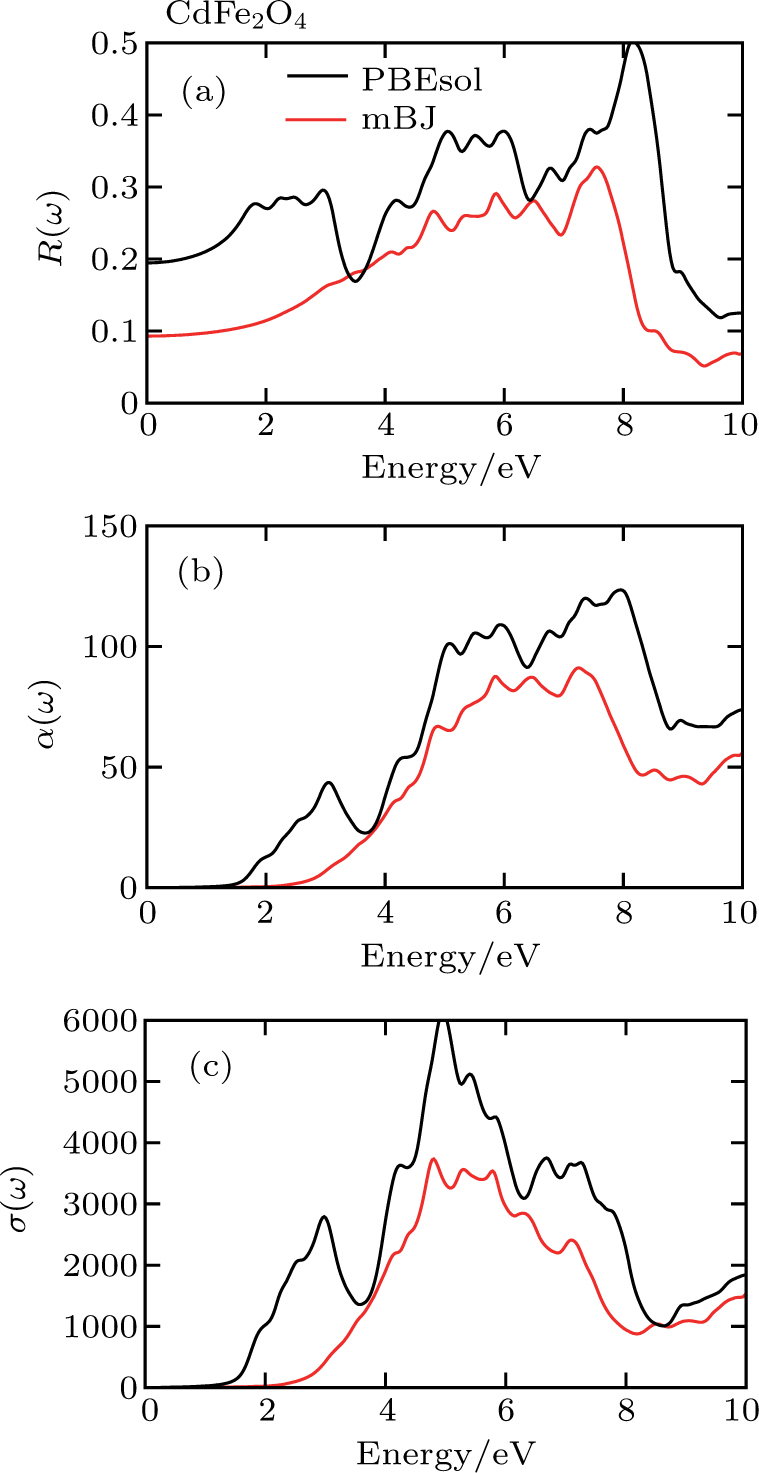
The details of the electronic transitions, illustrating material interactions with the impinging radiations w.r.t. in various symmetry directions of the first Brillion zone are observed through inter-and intra-band transitions, which cause varying excitation and de-excitation rates. While, the inter-band transitions are sufficient for precisely revealing the optical behaviors, and can be expressed by complex dielectric constant 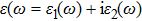
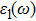
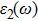




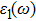
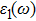
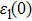
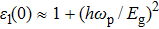
 | Fig. 5. (color online) (a) Reflectivity, (b) absorption coefficient, and (c) optical conductivity calculated for CdFe2O4 in FM phase by employing PBEsol and PBEsol + mBJ functional. |
The 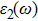
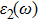

The refractive index n(ω) and extinction coefficient k(ω), as plotted in Figs. 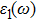


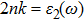
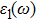
To probe surface quality, light reflected by the material surface is observed by computing reflectivity R(ω) using PBEsol and PBEsol + mBJ potentials, as presented Fig. 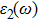
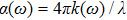
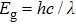
The optical conductivity, σ (ω), showing optically activated free charge carriers, is computed by using both potentials, as expressed in Fig. 
The imbalanced demand and supply chain of energy has stimulated researchers to search for the materials exhibiting high waste heat for useful energy conversion efficiencies. Such thermoelectric materials are gauged in terms of high electrical conductivity (σ/τ) and low thermal conductivity (κ/τ), to enhance the power factor 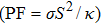
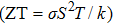
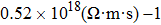
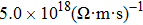
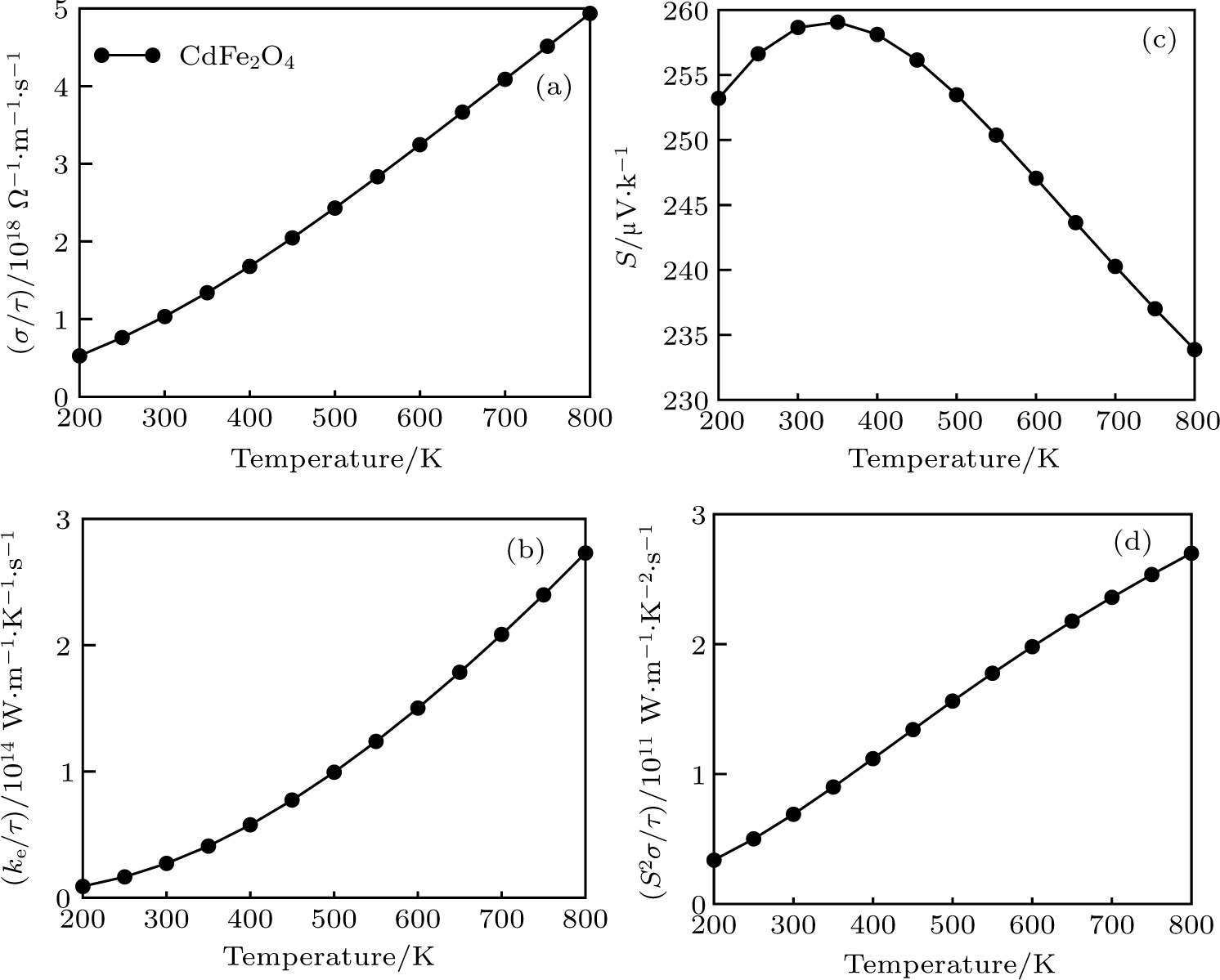 | Fig. 6. (a) Electrical conductivity, (b) Seebeck coefficient, (c) thermal conductivity, and (d) power factor extracted for CdFe2O4 by applying BoltzTraP code. |
As total thermal conductivity (κ /τ) arises due to both electrons and phonons, the Fourier law, written as 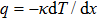
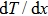
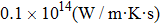
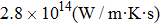
It is important to notice a potential difference (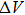
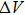
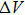

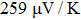
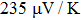
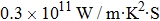
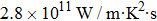
The density functional theory based on Wien2K code is applied for describing the electronic, magnetic and optical behaviors of CdFe2O4 by applying PBEsol and PBEsol + mBJ potentials. Thermoelectric properties computed by BoltzTrap code are also presented. Following important conclusions are drawn.
(i) The comparison of ground state energies in FM and AFM states confirms stable FM state, which is further verified by the negative enthalpy of formation.
(ii) The electronic behaviors illustrate metallic and semiconducting nature, according to the computations done by using PBEsol and PBEsol + mBJ potential, respectively.
(iii) The computed exchange energies are found higher than crystal field and John–Teller distortions evidence stable FM state. Similarly, negative pd-exchange energy shows strong hybridization elucidating the dominant role of the carrier spin.
(iv) The use of mBJ potential reveals that band gap operates in the visible energy revealing CdFe2O4 as s suitable candidate for optoelectronic industry.
(v) The computed PF exhibits very large values suggesting CdFe2O4 to be suitable for various applications, such as thermoelectric generators and refrigerators.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] |